Ex 7.11, 8 by using the properties of definite integrals, evaluate the integrals : A constant can be brought outside of the integral sign to simplify the integration. Integration of log(1 + tan x) from 0 to π/4 is equal to π/8 log 2.
What is the differentiation of 1/tanx? Quora
The integral of tan(x) can be solved by rewriting the equation as the integral of sin(x)/cos(x) dx, and then using the integration technique called substitution.
Integrate cos 2 x/(1+tanx) share with your friends.
Or connect using your email or mobile. In this equation, ln indicates the function for a natural logarithm, while cos is the function cosine, and c is a constant. I = ∫ 0 π / 4 l o g ( 1 + 1 − t a n x 1 + t a n x) d x. Common misconceptions > mindmap > memorization tricks > problem solving tips > important diagrams > practice more questions.
I can then use substitution to find it.
What is the integral root of cosx? Find the integral root of tanx? Ex 7.2, 4 ex 7.2, 5. Let i = \(\int_{0}^{\pi/4}\) log(1 + tan x) dx.
Using substitution, the value you will obtain as your answer will be.
Embibers login here to continue. I = ∫ 0 π / 4 l o g ( 2 1 + t a n x) d x. 2 qs > easy questions. X d x = sec.
The integration of secant tangent is of the form.
Substitute the values and you will get = log(secx) + c. The integral of tan (x) can be solved by rewriting the equation as the integral of sin (x)/cos (x) dx, and then using the integration technique called substitution. 1 tanx = cotx = cosx sinx. A common way to do so is to place thin rectangles under the curve and add the signed areas together.
= ∫ 1 u du.
Find the integral of root tanx? I = ∫ 0 π / 4 l o g ( 1 + t a n [ π 4 − x] d x. = ∫ cosx sinx dx. Target year 2017 2018 2019.
Where, c is the constant for integration
What is the integral of root tanx? ∫ 1 tanx dx = ∫cotxdx. Homework statement ∫[(1+tanx.tan(x+a)]dx homework equations the attempt at a solution ∫sec^x.tan(x+a) after that i don't know as i tried method of substitution by putting x+a=t but i am not getting the answer as its form on the whole remains same Since, this is a definite integral, to integrate it we have to use the following property of definite integrals.
An approximate solution can be expressed by finding the series expansion of the integral of e^{\tan (x)} around x = 0.
Let u = sinx, so du = cosxdx to get. Ex 7.2, 34 important → chapter 7 class 12 integrals (term 2) serial order wise; However, in cases of this type (definite integral with a complicated. Sometimes an approximation to a definite integral is desired.
1 qs > jee advanced questions.
Hence we substitute that into the equation and reintroduce the constant. Tan𝑥 )] 𝑑𝑥 i=∫_0^(𝜋/4) log[1+ Integration of the secant tangent function is an important integral formula in integral calculus, and this integral belongs to the trigonometric formulae. Ex 7.2, 1 ex 7.2, 2 ex 7.2, 3 important.
∫_0^(𝜋/4) log(1+tan𝑥 ) 𝑑𝑥 let i=∫_0^(𝜋/4) log〖 (1+tan𝑥 )〗 𝑑𝑥 ∴ i=∫_0^(𝜋/4) log[1+tan(𝜋/4−𝑥) ] 𝑑𝑥 i=∫_0^(𝜋/4) log[1+(tan 𝜋/4 −tan𝑥)/(1 +〖 tan〗 𝜋/4.
I will indicate or show that this integration problem has more than one solution in terms of special functions. ( x) d x = ( − c o s ( π)) − ( − c o s ( 0)) = 2. Split the single integral into multiple integrals. Limit asintegration of 1 to 2 (3x^2+5x)dx;
152 qs > medium questions.
Click here👆to get an answer to your question ️ integrate: As a remainder, if one wants to integrate a similar question, $\int_{0}^{\pi/2}\ 1/ (1+(tanx)^{\sqrt2})\ dx$, refer to this evaluate $\int_0^\pi\frac{1}{1+(\tan x)^\sqrt2}\ dx$. ∫ cos 2 x 1 + tan x d x = 1. We will be using a definite integral property for solving this question.
View chapter > shortcuts & tips.
Both of them were what i want to ask. This means ∫π 0 sin(x)dx= (−cos(π))−(−cos(0)) =2 ∫ 0 π sin.
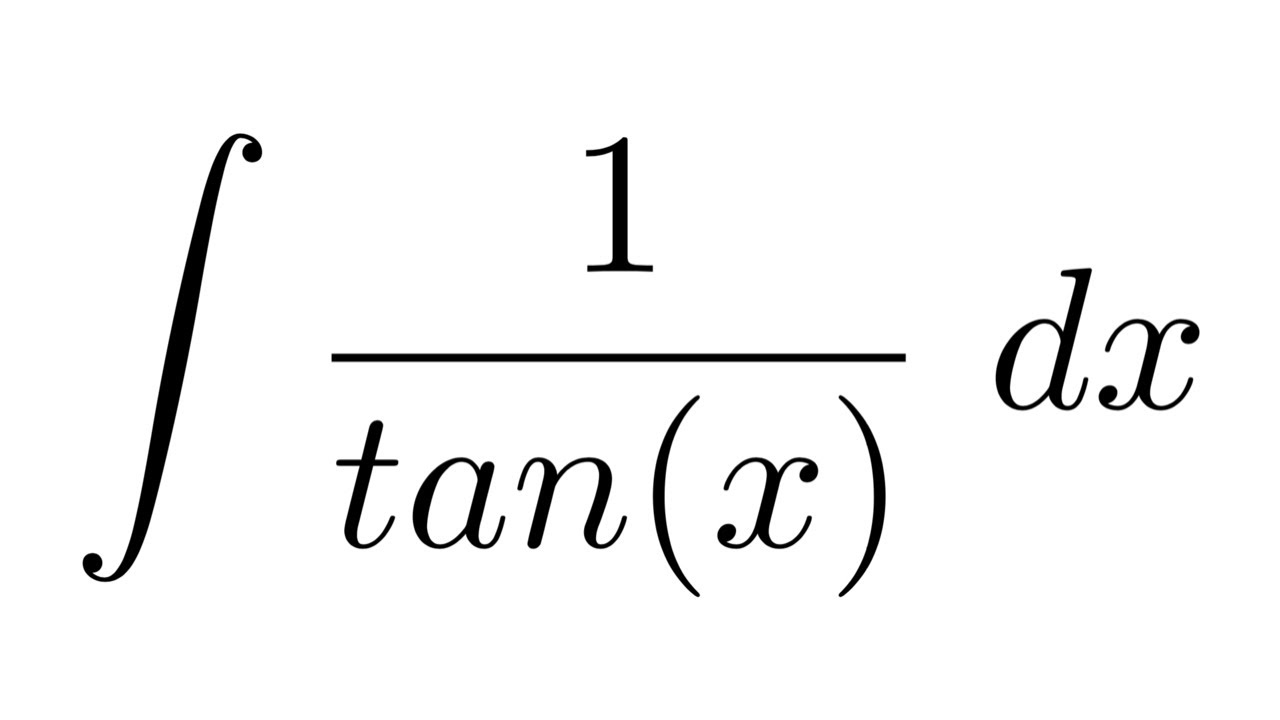
![Find the value of the integral of 1/[1 + cube(tanx)] where](https://i.ytimg.com/vi/6DKmCGhviDk/maxresdefault.jpg)


