An ellipse is defined as the locus of all points in the plane for which the sum of the distances r1 and r. A = 4 cm, and b = 2 cm. Since a = b in the ellipse below, this ellipse is actually a circle whose standard form equation is x² + y² = 9 graph of ellipse from the equation the problems below provide practice creating the graph of an ellipse from the equation of the ellipse.
Ellipse Formula Derivation
Where (c = half distance between foci) c a 0 e 1.
To determine the eccentricity and the length of the latus rectum of an ellipse.
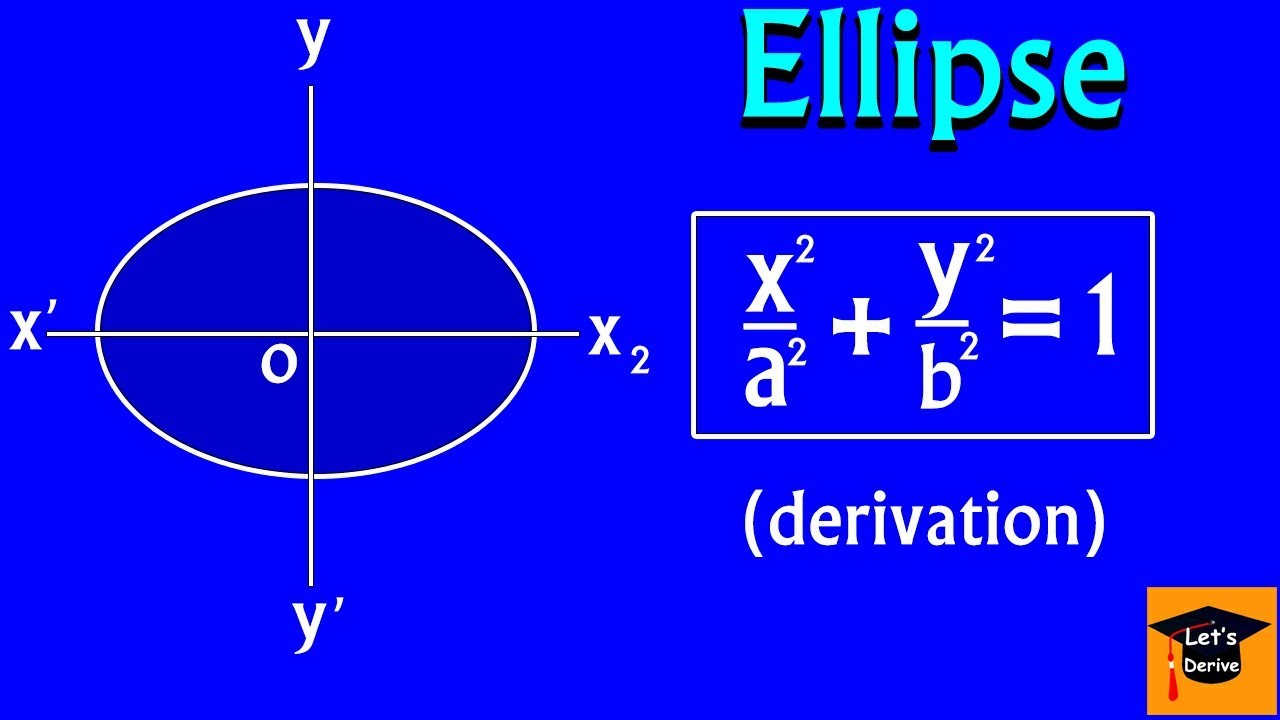
X2 a2 + y2 b2 = 1. Y = sin(bx) the sine wave is b times thinner. Derivation continuity equation for cartesian coordinates. Area of ellipse = πab derivation of area of an ellipse.
Equation of ellipse solved examples solution:.
X2 a2 + y2 b2 = 1 x 2 a 2 + y 2 b 2 = 1. Ellipse standard equations of ellipse. Y = sin x b the sine wave is b times wider. (center at x = 0 y = 0) the eccentricity e of an ellipse:
There are several ways to derive the equation of the polarization ellipse.
As a result, the ellipsoid eqn doesn't have a derivation comparable to that of the ellipse. Further, let’s square both sides. Then the ellipse is a hyperbola. The derivation of the standard form of the equation of an ellipse relies on this relationship and the distance formula.
The sphere stretched by factors $a$, $b$, $c$ in the coordinate directions has equation $(x/a)^2+(y/b)^2+(z/c)^2=1$.
Azzam's seminal 'ellipsometry and polarized light' first expresses the field in terms of two components (parallel and perpendicular to established basis vectors): The formula for eccentricity of a ellipse is as follows. Period (wavelength) is multiplied by b. This equation defines an ellipse centered at the origin.
In this instance, the coordinates of the center of the ellipse are also given as ( h,k ).
Derivation of standard equation of ellipse. The derivation described in r.m.a. Frequency is multiplied by b. Equation of ellipse is x2/a2+ y2/b2= 1.
Then the ellipse is a parabola.
The only difference between the circle and the ellipse is that in a circle there is one radius, but an ellipse has two: Period (wavelength) is divided by b. Derive the equation of an ellipse. Derivation of the equation given are two points on the and , the foci, both units away from their center.
University of minnesota general equation of an ellipse.
The set of all points , whose distances from and from add up to a certain constant, is called an ellipse. The directrix of the ellipse can be derived from the equation of the ellipse in two simple steps. The points and are called the foci of the ellipse. E ∥ = a 1 cos.
Thus, the standard equation of an ellipse is [latex]\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1[/latex].
Derivation of equations of ellipse. If [latex]a>b[/latex], the ellipse is stretched further in the horizontal direction, and if [latex]b>a[/latex], the ellipse is stretched further in the vertical direction. X2b2 a2b2 + a2y2 a2b2 = a2b2 a2b2 x 2 b 2 a 2 b 2 + a 2 y 2 a 2 b 2 = a 2 b 2 a 2 b 2. The given equation of the ellipse is x 2 /25 + y 2 /16 = 1.
The equation of normal to the given ellipse whose slope is ‘m’, is.
In this video we derive the equation of an ellipse. Eccentricity standard equations of ellipse latus rectum. See parametric equation of a circle as an introduction to this topic. This is how to derive the equation of an ellipse when the horizontal major axis is centered at the origin.
( ω t) − a 2 cos.
The equation of the ellipse is \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\). X2 16 + y2 9 = 1. From this we can find the value of 'a' and also the eccentricity 'e' of the ellipse. The derivation is beyond the scope of this course, but the equation is:
Then the ellipse is a circle.
By considering one of the points of the ellipse which lies on the major axis we can conclude that, $$ r+r'=2a.$$ if $\theta$ is the angle between $\vec{r}$ and the line connecting $f$ to $f$ ' then we can use the law of cosines to write, Let be a point on the ellipse. Just as with the circle equations, we subtract offsets from the x and y terms to translate (or move) the ellipse back to the origin. The equation of the ellipse is:
Then it is an ellipse.
The general equation of ellipse is: Derive the equation of a parabola. Comparing this with the equation of the ellipse x 2 /a 2 + y 2 /b 2 = 1, we have a 2 = 25, and b 2 = 16.