Power = work / time and work done on a body is equal to the energy expended on it so; Water gains 200 j of heat energy, the kettle has done (at least) 200 j of work. Power = work done (j) / time taken (s) simplified formula:
Electrical Energy
Power is the energy you need to complete a given task.
Click create assignment to assign this modality to your lms.
The unit of power is the watt (w), which is equal to a joule per second (j/s). Changing energy to kinetic energy the formula becomes; Where, p is the power (work done per unit time) τ is the torque (rotational ability of a body) ω is the angular velocity (rate of change of angular displacement). Each time “work” is done, energy is transferred from one place to another.
Click here to view we have moved all content for.
Work (w) this is the total energy transferred or work done. Work done = force x distance. Watt (w) power can also be defined in terms of force and velocity. The formula used by this calculator to determine the power from the work done and time taken is:
Power is expressed in the equation:
It is equal to the amount of work done divided by the time it takes to do the work. This is because energy is the ability to do work. P = w / t. We have a new and improved read on this topic.
Work done / time taken = force x (displacement / time taken)
Power = (m * v^2) / 2 * t T = total time taken. You lift up a 5 kg mass 1m high, this mass gains 50 j of gravitational potential energy. Power = energy / time.
You can use this formula to calculate power, energy transferred/ work, or time taken if you have two of these three values.
Work done is denoted by ‘w’, time is denoted by ‘t’ and the rate of work is denoted by ‘r’. Total work done (w) = power (p) x time (t) or. The definition of work is the power you apply to displace an object over a distance in a given time. W = work (joules) θ = angle.
The amount of work done is expressed in the equation:
If w = f d w = f d and work can be expressed in j, then p = w t = f d t p = w t = f d t so power can be expressed in units of n ⋅ m s n ⋅ m s. K = p (1) t = m (2) p = w/t (3) now, do a few simple substitutions: W = p · t. After doing so, the equation we are left with is:
Power = (1/2 * mass of the body * the square of its velocity)/ time.
This quantity, the rate at which work is done, is defined as power. The formula used by this calculator to determine the work done from the power output and elapsed time is: Power is a measure of how quickly work is done. Power is the ratio between the work done and the time taken and can be expressed as.
The basic formula for work done in a given time is equal to the product of time and rate of work.
The equation used to calculate power is: Work done (w) = time(t) x rate of work (r). P = w/t, like p = e/t. Power (p) this is the rate at which energy is transferred.
Click here to go to the next topic.
Time (t) this is the total elapsed time. F = force applied on the body. Work = force ( f ) × displacement(s) p = f × s/t. \ [power = \frac {work~done} {time}\] \ [power = \frac {w} {t}\] this is when:
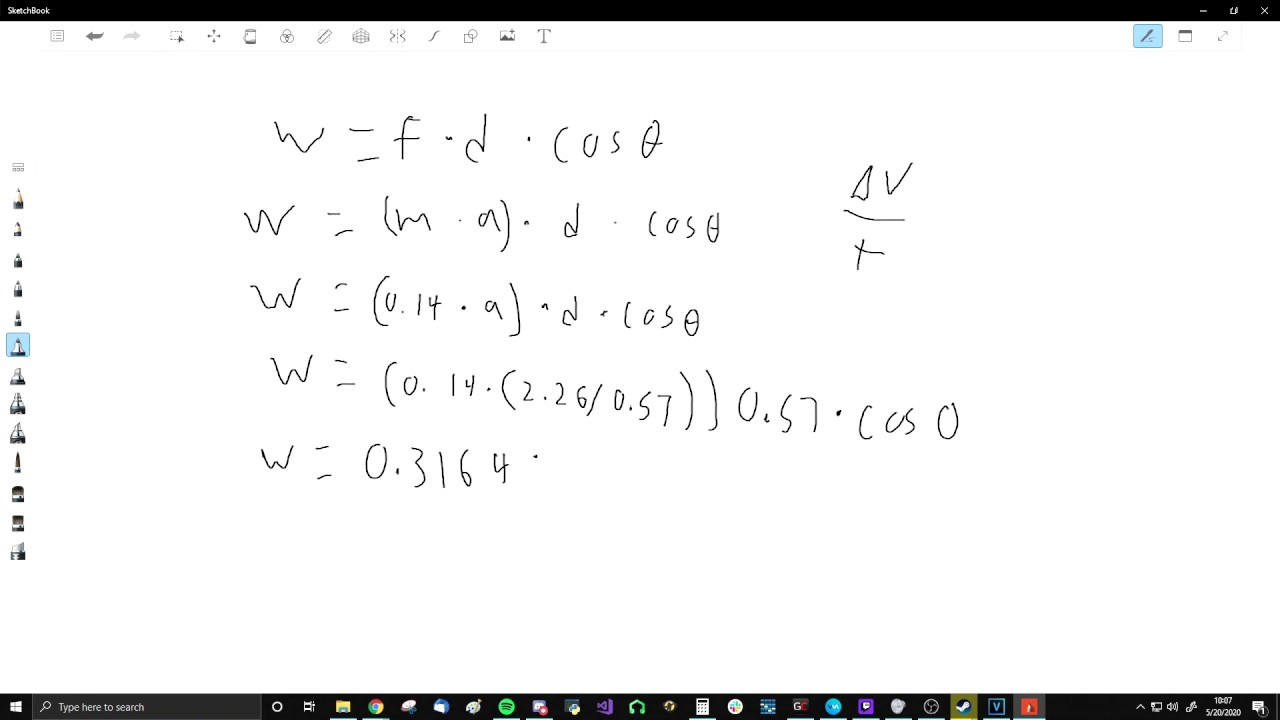
P = power (w, or j/s) ∆w = the work done, or energy used (j) ∆t = the time taken to do the work (s) power formula questions:
Work = displacement x force. This equation is derived by simply dividing both sides of the equation for work done by the time taken. Work done is directly proportional to the time and rate of work. W = work done by the body.
Power and how it relates to work and time, how to calculate power and the unit called horsepower.
Equations for power from this very simple definition, we can come up with a simple equation for the average power of a system. P = w / dt = t θ / dt = t ω = 2 π n t = 2 π (n rpm / 60) t = 0.105 n rpm t (3) where. Power = work done / time taken. You've done 50 j of work against gravity.
W = work done or energy transferred;
Power (p) is measured in watts (w). Represent the dot product or scalar product. R = radius (m) t = torque or moment (nm) power transmitted. Where p is power in watts (w), e is the energy expended or work done in joules (j), and t is the time take in seconds (s).
The triangle above may help you to rearrange the equation.
So, substituting algebraic equations for these time worn bits of wisdom, we get: Let us start from the formula which define power as the rate work is done. If the system does an amount of work, w, over a period of time, t, then the average power is simply given by: Work done = 10 × 2 = 20 j.
S = total displacement of the body.
Power = work done upon time. Work done is sort of like 'energy spent'. The work done per day is called the rate of work.