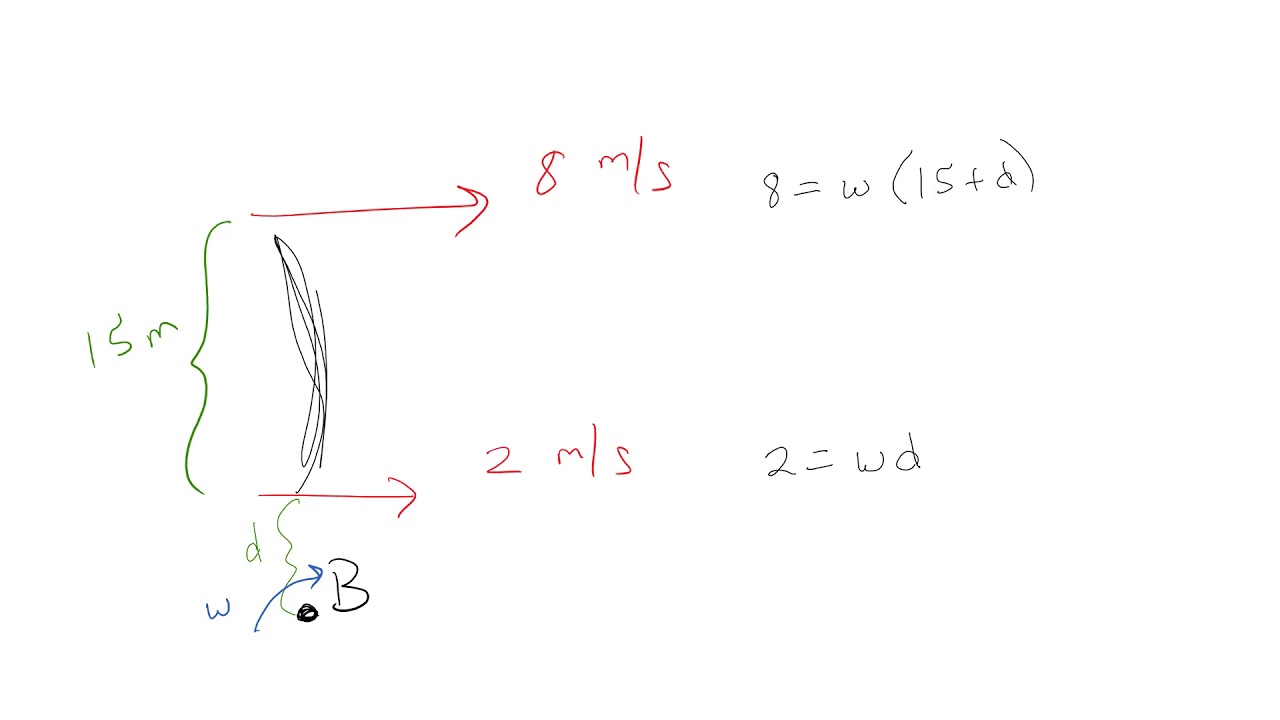This point is called the instantaneous center (ic) of zero velocity. You throw a pencil up in the air and at the apex of the projectile, the velocity will always be zero but because of acceleration due to gravity (9.81m/s^2), the acceleration will never be zero. Instead, they are both less than its average velocity.
Instantaneous Acceleration YouTube
A ball is thrown straight up in the air.
Earn 10 reputation (not counting the.
As far as i can tell, not really. The point is nam ed instantaneous center of zero So, the instantaneous speed of the ball is maximum when it is at the lowest position and zero at its highest position. It is possible that the instantaneous velocity is never zero in the interval.
In region 4, we negatively accelerate to.
Therefore, this point must not be used to calculate accelerations. It can also be said that the instantaneous acceleration is the limit what have the average acceleration (the division of the change in speed by the time that elapses when advancing between two. In our graph above (region 1), we start with a velocity of 0 m/s (at rest) and accelerate to 10 m/s in 10 seconds. That is, acceleration is zero when the velocity of the object is constant.
The instantaneous velocity will be zero if there is a quick motion without acceleration in a short span.
When an object is accelerating, its instantaneous velocity will not be equal to its average velocity; We define this point as the instantaneous center of zero. So, we can easily determine when the acceleration is positive, negative, and zero, just by looking at the angle θ at. We can show this graphically in the same way as instantaneous velocity.
It may or may not lie on the body!
We see that average acceleration. If the body is in a motion but a part of it is connected rigidly to a certain point on another object, then the instantaneous velocity of that object is zero at that point. In view (a), instantaneous acceleration is shown for the point on the velocity curve at maximum velocity. In region 3, we accelerate to 20 meters per second in 4 seconds.
The velocity would not be constant though.
The instantaneous acceleration of an object is the limit of the average acceleration as the elapsed time approaches zero, or the derivative of velocity v with respect to t: At some moment, if the velocity of an object is zero, must its (instantaneous) acceleration be zero? We can show this graphically in the same way as instantaneous velocity. At this point, instantaneous acceleration is the slope of the tangent line, which is zero.
Instantaneous acceleration equal to zero at that particular instant.
At some moment, if the velocity of an object is zero, can its (instantaneous) acceleration be nonzero? Instantaneous velocity can be equal to average velocity when the acceleration is zero or the velocity is constant, because all instantaneous velocities are equal to each other and likewise to the average velocity in this case. If the speed was anything above zero, you could be accelerating in a circle and therefore keep the speed constant. If the instantaneous velocity of a particle is zero, will its instantaneous acceleration be necessarily zero?
If the location of this point can be determined, the velocity analysis can be simplified because the body appears to rotate about this point at that instant.
The instantaneous acceleration, therefore, reflects the acceleration that has an object at a specific time and at a specific point of its trajectory. The slope of the tangent line is zero, and therefore the instantaneous acceleration is zero. When the rigid body moves in plane with angular velocity, ω, which is unequal to zero, we choose a point , c, in the. In view (a), instantaneous accelerationis shown for the point on the velocitycurve at maximum velocity.
In region 2, we remain at 10 meters per second for 10 more seconds.
Thus, similar to velocity being the derivative of the position function, instantaneous acceleration is the derivative of the velocity function. Body for which the instantaneous acceleration is zero. At any other time, the slope of the tangent line—and thus. No, it will no be zero because at highest point of vertical is zero but its instantaneous acceleration is not zero.
The average velocity of a particle moving on a straight line is zero in an interval.
In a two dimensional motion,instantaneous speed `v_(0)` is a positive constant.then which of the following are necessarily true? Asked jan 16, 2021 in physics by takshii (35.1k points) motion in a straight line; It is possible that the instantaneous acceleration is never zero in the interval. Instantaneously zero (if it is rigidly connected to the body).
The problem here is that you are defining the.
Also, you can see that the slope of the tangent line decreases to zero while the ball is going up and increases while it is going down. Also in part (a) of the figure, we see. At any other time, the slope of the tangent line—and thus instantaneous acceleration—would not be zero. The position of point aand pare illustrated in fig.
At some moment, if the acceleration of an object is zero, must its (instantaneous) speed or velocity be zero?
For which of these situations is/are both the instantaneous velocity and the acceleration zero? Derive the formula of instantaneous acceleration (step by step) At this point, instantaneous accelerationis the slope of the tangent line, which is zero.