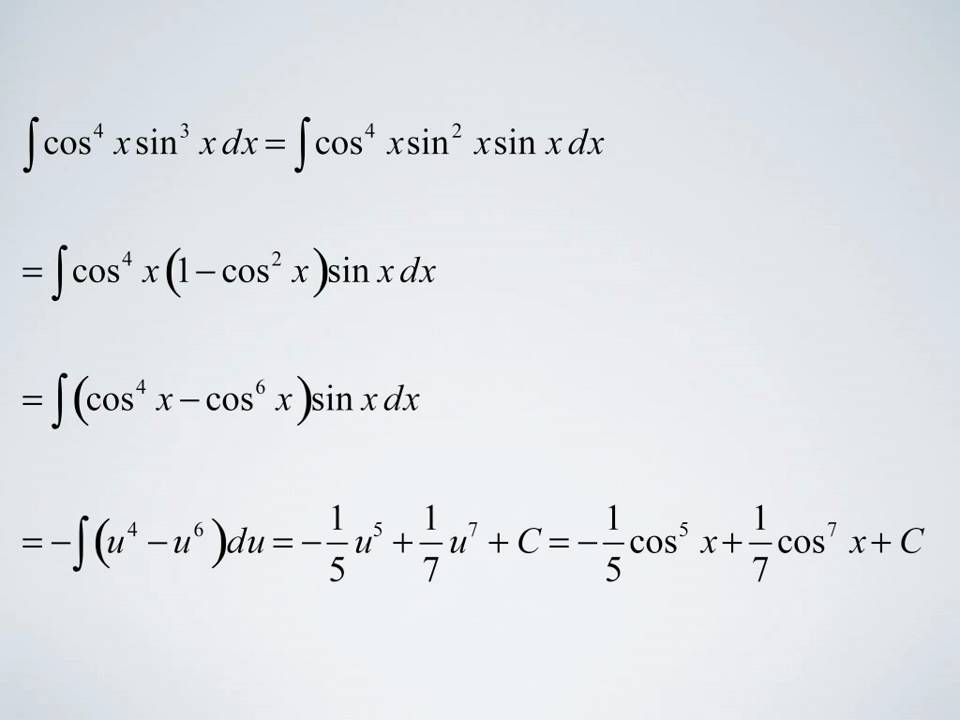Cos(ax)cos(bx)dx = 1 2 sin((a b)x) a b + sin((a+b)x) a+b +c. 1 + tan 2 x = sec 2 x. Or, you could rewrite the integrand only in terms of a single trigonometric function.
Trig Integrals
Integration rules and techniques antiderivatives of basic functions power rule (complete) z xn dx= 8 >> < >>:
1 2 sin((a+b)x)+sin((a b)x) dx = 1 2.
Integrating products of sines and cosines of different angles to integrate products involving sin ( a x ) , sin ( a x ) , sin ( b x ) , sin ( b x ) , cos ( a x ) , cos ( a x ) , and cos ( b x ) , cos ( b x ) , use the substitutions ∫ tan n x d x = ∫ tan n − 2 x tan 2 x d x = ∫ tan n − 2 x ( sec 2 x − 1) d x = tan n − 1 x n − 1 − ∫ tan n − 2 x d x. Sin(ax)sin(bx)dx = 1 2 sin((a b)x) a b. D dx sin(x) = cos(x) d dx cos(x) = sin(x) but also:
If the power of the sine is odd and positive:
Integration using trigonometric identities practice problems if you're seeing this message, it means we're having trouble loading external resources on our website. Trigonometric integrals r sin(x)dx = cos(x)+c r csc(x)dx =ln|csc(x)cot(x)|+c r cos(x)dx =sin(x)+c r sec(x)dx =ln|sec(x)+tan(x)|+c r tan(x)dx =ln|sec(x)|+c r cot(x)dx =ln|sin(x)|+c power reduction formulas inverse trig integrals r sinn(x)=1 n sin n1(x)cos(x)+n 1 n r sinn2(x)dx r sin1(x)dx = xsin1(x)+ p 1x2 +c r cosn(x)=1 n cos n 1(x)sin(x)+n 1 n r cosn 2(x)dx. 2 22 a sin b a bx x− ⇒= θ cos 1 sin22θθ= − 22 2 a sec b bx a x− ⇒= θ tan sec 122θθ= − 2 22 a tan b a bx x+ ⇒= θ sec 1 tan2 2θθ= + ex. If n6= 1 lnjxj+ c;
Xn+1 n+ 1 + c;
If a 6= b, then: Cos((a b)x) a b +c the other integrals of products of sine and cosine follow similarly. Review trigonometric identities 1 trigonometric derivatives we rst need to review the derivative rules for trigonometric functions. For the following, let u and v be functions of x, let n be an integer, and let a, c, and c be constants.
∫sec x dx = ln|tan x + sec x| + c.
These integrals are evaluated by applying trigonometric identities, as outlined in the following rule. (use antiderivative rule 7 from the beginning of this section on the first integral and use trig identity f from the beginning of this section on the second integral.) (now use antiderivative rule 3 from the beginning of this section.). For a complete list of antiderivative functions, see lists of integrals. ∫ − 1 1 d x ( 1 + x 2) 2.
16 x2 49 x2 dx ∫ − 22 x = ⇒ =33sinθ dx dcosθθ
Generally, if the function is any trigonometric function, and is its derivative, in all formulas the constant a is assumed to be nonzero, and c denotes the constant of integration. Integrals involving sec(x) and tan(x): The important rules for integration are: If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions.
Use trigonometric identities to integrate sin2 x, cos2 x, and functions of the form sin 3x cos 4x.
We may also use a trigonometric substitution to evaluate a definite integral, as long as care is taken in working with the limits of integration: There are two which are the most important and come up the most: We will use the following trigonometric identities: Z ex dx= ex + c if we have base eand a linear function in the exponent, then z eax+b dx= 1 a eax+b + c trigonometric functions z sin(x)dx= cos(x) + c z
D dx sec(x) = sec(x)tan(x) d dx tan(x) = sec2(x) d dx csc(x) = csc(x)cot(x) d dx cot(x) = csc2(x) 2 ad hoc integration
Below are the list of few formulas for the integration of trigonometric functions: Sin 2 x = 1 − cos 2 x 2. ∫cos x dx = sin x + c. ∫ln(x) dx = x ln(x) − x + c;
It is assumed that you are familiar with the following rules of differentiation.
Then θ = tan − 1. Contents 1 integrals involving only sine 2 integrands involving only. ( x 2), where we specify 0 ≤ θ < π / 2 or π ≤ θ < 3 π / 2. The power of the integrand can be reduced using the trigonometric identity.
Integrals involving sin(x) and cos(x):
The different rules for integration of exponential functions are: Convert the remaining factors to cos( )x (using sin 1 cos22x x.) 1. You could utilize the following identities: ∫tan x dx = ln|sec x| + c.
∫sec 2 (x) dx = tan(x) + c;
\end{eqnarray*} we have six general integrals to evaluate to prove the orthogonality of the set $\{1, ~\cos x, ~\sin x, \ldots\}$. ∫cot x dx = ln|sin x|. These allow the integrand to be written in an alternative form which may be more amenable to integration. Note that d x = 2 sec.
∫cos(x) dx = sin(x) + c;
∫a x dx = a x /ln(a) + c; Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities. Then θ = sec − 1. If n= 1 exponential functions with base a:
Z ax dx= ax ln(a) + c with base e, this becomes:
Cos 2 x = 1 + cos 2 x 2. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked. These formulas are meant to simplify the tough calculations of calculus with the utmost ease and this is the reason why every student starts with all basic formulas of integration. Integral formula for trig identities if you are a mathmatics students then you can easily get the significance of integration formulas.
A definite integral is used to compute the area under the curve these are some of the most frequently encountered rules for differentiation and integration.
Integrals of the form ∫ tan n x d x. \cos^ {2} x = \frac { 1+ \cos 2x} {2} cos2 x = 21+cos2x. Save a du x dx sin( ) ii. Let’s first notice that we could write the integral as follows, ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x.
Now recall the trig identity, cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x.
∫e x dx = e x + c;