Step 3 calculate adjacent / hypotenuse = 6,750/8,100 = 0.8333. Where b and p are the base and height of the triangle respectively. Also known as pythagoras's theorem this states that in a right trianglethe square of the hypotenuse “c” (the side opposite the right angle) equals the sum of the squares of the other two sides “a” & “b”, thus its equation can be written as presented here:
Right Triangle & Angles eyleMMath
Area = 30 in 2.
The area of a scalene triangle can be calculated using the length of its base and its height:
Using the area of a triangle formula, area = (1/2) × b × h. (it is the edge opposite to the right angle and is c in this case.) where (for brevity) it says 'edge a', 'angle b' and so on, it should, more correctly, be something like 'length of. The most important formulas for solving problems with scalene triangles with right angles are the area formula, the perimeter formula, and the pythagorean theorem. In a right triangle, one of the angles has a value of 90 degrees.
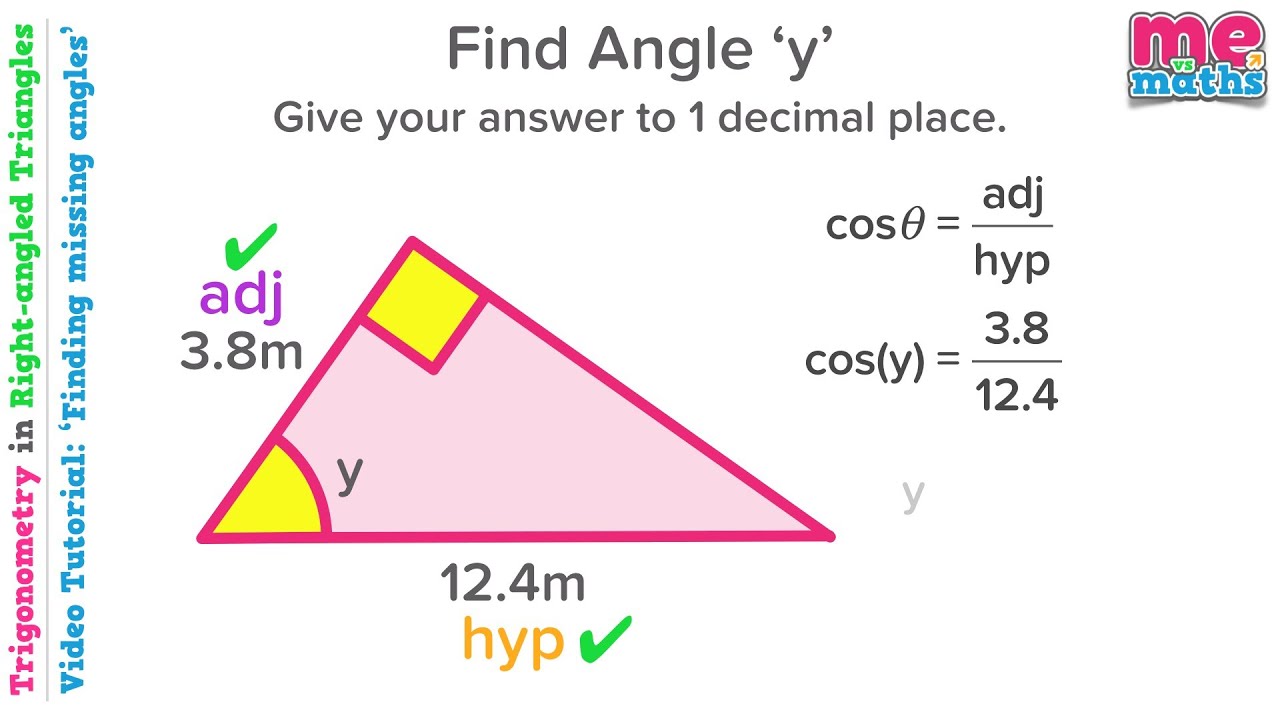
Step 2 soh cah toa tells us to use c osine.
(opens a modal) using similarity to estimate ratio between side lengths. Csc a = hypotenuse / opposite = c / a. This formula has given the pythagoras triplets such as 3, 4, 5. It states the square of the hypotenuse is equal to the sum of the squares of the other two sides.
The pythagoras formula is (hypotenuse) 2 = (base) 2 < + (altitude) 2.
Explore right angle triangle formula in mathematics and solve it numerically by entering known parameter in the calculator. Formulas used for calculations on this page: 3 2 + b 2 = 5 2. Pick the option you need.
Sec a = hypotenuse / adjacent = c / b.
For example, an area of a right triangle is equal to 28 in² and b = 9 in. A 2 + b 2 = c 2. The right angled triangle formula is given by (hypotenuse) 2 = (adjacent side) 2 + (opposite side) 2 = (20) 2 + (15) 2 = 400 + 225 = 625 cm hypotenuse = Α = 34.66° β = 55.34° now, let's check how does finding angles of a right triangle work:
Sin (b) = b/c, cos (b) = a/c, tan (b) = b/a.
There are also special cases of right triangles, such as the 30° 60° 90, 45° 45° 90°, and 3 4 5 right triangles that facilitate calculations. The definition is very simple and might even seem obvious for those who already know it: Height = 12 in, hypotenuse = 13 in. Getting ready for right triangles and trigonometry.
Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be.
The 60° angle is at the top, so the h side is adjacent to the angle! Given a = 3, c = 5, find b: Tan a = opposite / adjacent = a / b. Area = (1/2) × 5 × 12.
The most common and versatile are the law of cosines and the law of sines.
Formulas for right angle scalene triangles. Our right triangle side and angle calculator displays missing sides and angles! Assume that we have two sides. Calculate the length of a hypotenuse if given legs and angles at the hypotenuse ( c ) :
(opens a modal) side ratios in right triangles as a function of the angles.
The perimeter of a right triangle:s = a + b + c. Sin a = opposite / hypotenuse = a / c. \(a = \frac{1}{2} b \times p\). Trigonometry ratios (sohcahtoa) pythagorean theorem vs sohcahtoa (which to use) sohcahtoa only applies to right triangles ( more here).
Let us now look at the right triangle formula.
Calculate the length of a leg if given other sides and angles ( a b ) : Step 1 the two sides we know are a djacent (6,750) and h ypotenuse (8,100). Step 1 the two sides we are using are a djacent (h) and h ypotenuse (1000). Actually, the relation between the angles and sides is the base for trigonometry.
The three known parameters may either be two side lengths and an angle or two angles and a side length.
A 2 + b 2 = c 2. (opens a modal) hypotenuse, opposite, and adjacent. Area of a right triangle: First things first, let's explain what a right triangle is.
Where a and b are two sides of a triangle, and c is the hypotenuse, the pythagorean theorem can be written as:
Area = a*b/2, where a is height and b is base of the right triangle. The pythagorean theorem, a2 +b2 = c2, a 2 + b 2 = c 2, is used to find the length of any side of a right triangle. A 2 + b 2 = c 2. How do you find the area of a right.
Calculate the length of sides of a right triangle using pythagorean theorem ( c a b ) :
Step 3 put our values into the cosine equation: Sin (a) = a/c, cos (a) = b/c, tan (a) = a/b. The longest side of a right triangle is called the hypotenuse, and it. Step 2 soh cah toa tells us we must use c osine.
Cos a = adjacent / hypotenuse = b / c.