The sine angle formula is, \[\large sin\,\theta=\frac{opposite}{hypotenuse}\] solved examples Give your answer correct to 2 decimal places. = digit 1 2 4 6 10 f.
How to Calculate the Sides and Angles of Triangles Owlcation
Cos 2 (a) + sin 2 (a) = 1.
\[\text{area of a triangle} = \frac{1}{2} bc \sin{a}\] \[\text{area} = \frac{1}{2} \times 7.1 \times 5.2 \sin{42}\] area = 12.4 cm 2
Calculate the side of a triangle if given two other sides and the angle between them ( cosine rule) ( a ) : In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of a triangle to the sines of its angles. Remember that the given angle must be between the two given sides. If a + b = 180° then:
The following is the formula for the law of sines:
Tan (30°) = 1 / 1.732 = 0.577. Sine and cosine apply to an angle, any angle, so it's possible to have two lines meeting at a point and to evaluate sine or cosine for that angle even though there's no triangle as such. The longest side is the hypotenuse and the opposite side of the hypotenuse is the opposite side. In a formula, it is written as 'sin' without the 'e':
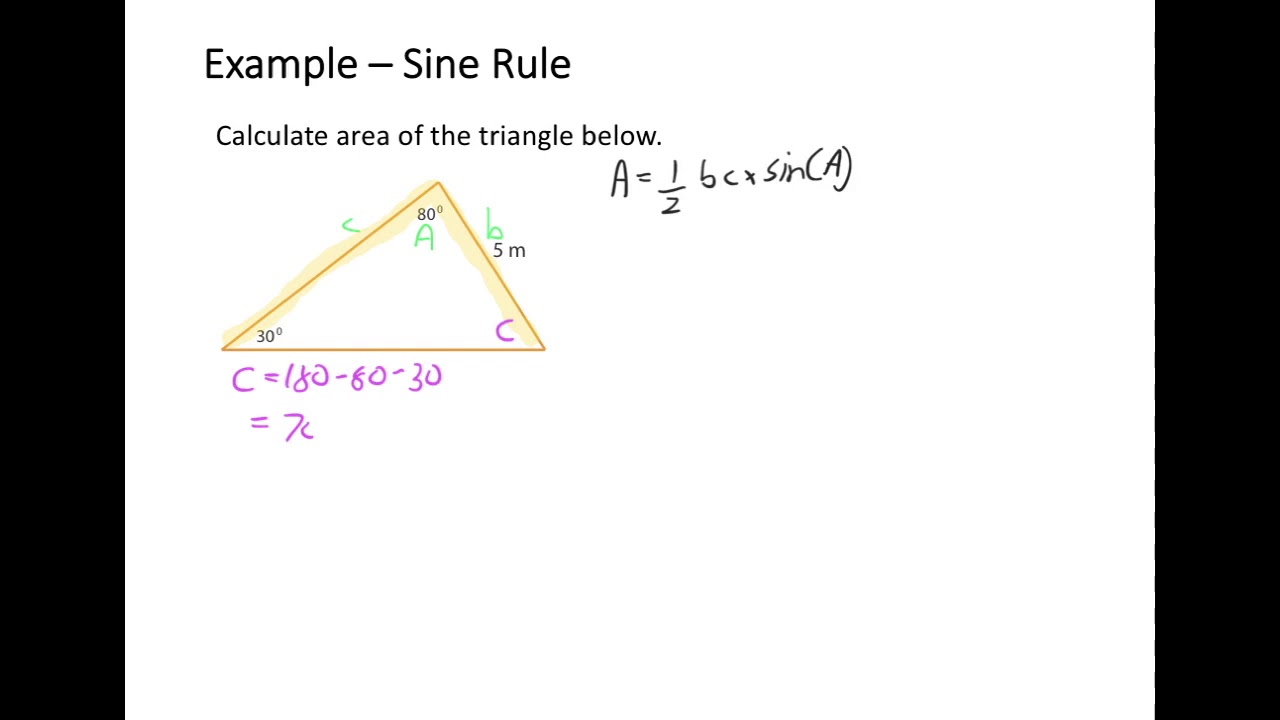
Calculate the side of a triangle if given side and any two angles ( sine rule ) ( a ) :
The law of cosines generalizes the pythagorean formula to all triangles. Sin value table is given below: Sin (θ + 2nπ) = sin θ for every θ. They’re called the law of cosines and the law of sines.
What are the sine, cosine and tangent of 30° ?
Find the area of triangle pqr if p = 6.5 cm, r = 4.3 cm and ∠ q = 39˚. Here are the formulas of sin, cos, and tan. When the height and the base side of the right triangle are known, we can find the sine, cosine, tangent, secant, cosecant, and cotangent values using trigonometric formulas. Enter sides a and b and angle c in degrees as positive real.
There are two main ways in which trigonometric functions are typically discussed:
The sine of an angle is a function that relates to the sides of a right triangle. Here c = [latex]30^ {\circ} [/latex], b = [latex]48.6^ {\circ} [/latex], a = [latex]101.4^ {\circ} [/latex]. In any right triangle , the sine of an angle x is the length of the opposite side (o) divided by the length of the hypotenuse (h). Sin (−θ) = − sin θ.
Specifically, the sine is found by taking the side that is opposite the angle and dividing it by the hypotenuse of the triangle.
Sine is the ratio of the opposite side to the hypotenuse side of the right triangle. These formulas help in giving a name to each side of the right triangle. Let's learn the basic sin and cos formulas. Up to 10% cash back sin ( a ) = opposite side hypotenuse = h c sin ( a ) = h c ⇒ h = c sin ( a ) substituting the value of h in the formula for the area of a triangle, you get r.
Area of triangle = ½ ab sinc.
Basic trigonometric identities for sine and cos. [latex]a=\frac {12sin\, 101.4^ {\circ}} {sin\,48.6^ {\circ}} [/latex] = 15.7 (1 d.p.) case 2. In trigonometry, sin is the shorthand of sine function. Where, a, b, c represent the lengths of the sides of the triangle and a, b, c represent the angles of the triangle.
The area area of a triangle given two of its sides and the angle they make is given by one of these 3 formulas:
Area = (1 / 2) b c sin (a) = (1 / 2) c a sin (b) = (1 / 2) a b sin (c) how to use the calculator. Side of a triangle : Sine, written as sin(θ), is one of the six fundamental trigonometric functions. Sin θ = perpendicular / hypotenuse.
According to the law, a sin α = b sin β = c sin γ = 2 r, {\displaystyle {\frac {a}{\sin {\alpha }}}\,=\,{\frac {b}{\sin {\beta }}}\,=\,{\frac {c}{\sin {\gamma }}}\,=\,2r,} where a, b, and c are the lengths of the sides of a triangle, and α, β,.
Outside the triangle, the sine function can be used to find the y component of a vector that has any angle. The classic 30° triangle has a hypotenuse of length 2, an opposite side of length 1 and an adjacent side of √ 3: Area of triangle pqr = ½ pr sinq = ½ × 6.5 × 4.3 × sin 39˚ = 8.79 cm 2 It says that c 2, the square of one side of the triangle, is equal to a 2 + b 2, the sum of the squares of the the other two sides, minus 2ab cos c, twice their
However, sine and cosine are derived from the sides of an imaginary right triangle superimposed on the lines.
[latex]\frac {a} {sin\, a}=\frac {b} {sin\, b} [/latex] from which. We use the sine rule in the form. Cos (30°) = 1.732 / 2 = 0.866. The law of sines formula is an equation that relates the sides of a triangle to the sines of their respective angles.