Cos θ = adjacent side/hypotenuse = ab/ac; Area of abc = 1 2absinc. Sine θ = opposite side/hypotenuse = bc/ac;
Section 4 Sine And Cosine Rule Math formulas, Teaching
The sine of an angle is a function that relates to the sides of a right triangle.
We can now rearrange these for h.
A sin a = b sin b = c sin c. The law of cosines generalizes the pythagorean formula to all triangles. Sine rule (the law of sine): Now, the formulas for other trigonometry ratios are:
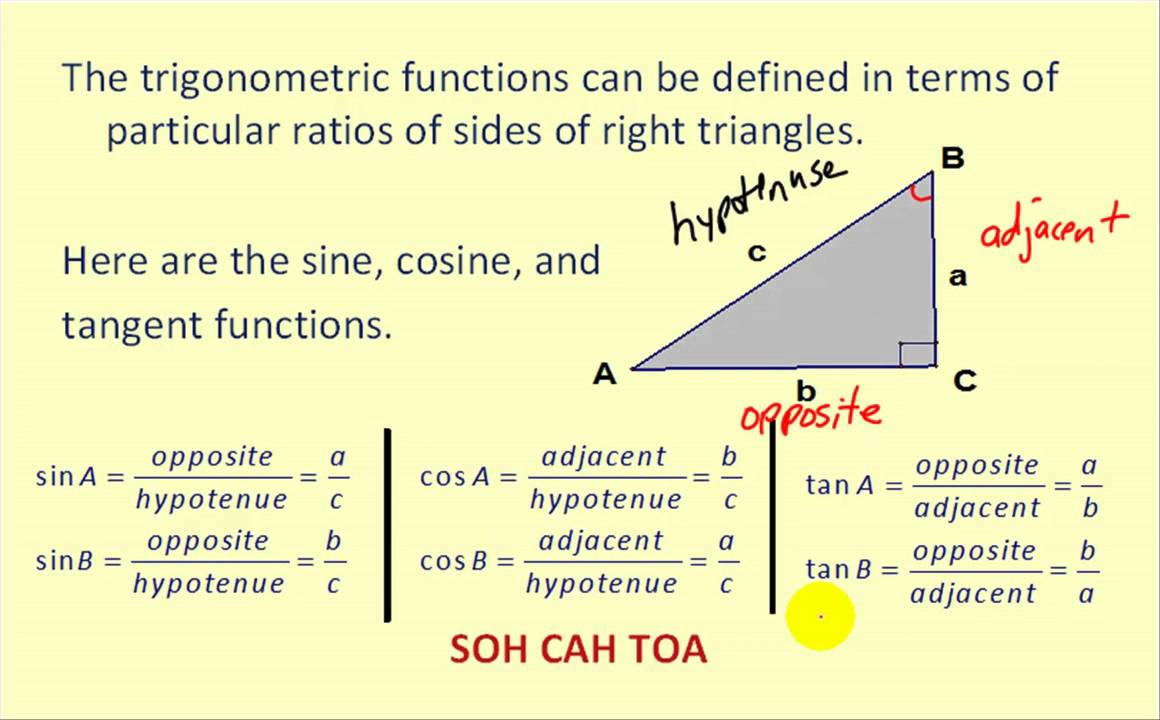
A, b and c are sides.
In any triangle a b c, a sin a = b sin b = c sin c , where a, b, c are side lengths. Cot θ = 1/tan θ = adjacent side/ side opposite = ab/bc; Cos 2 ( θ ) + sin 2 ( θ ) = 1 {\displaystyle \cos ^ {2} (\theta )+\sin ^ {2} (\theta )=1} where sin 2 ( x) means (sin ( x )) 2. Side c faces angle c).
A = c * sin(α) or a = c * cos(β) b = c * sin(β) or b = c * cos(α) given angle and one leg;
Calculate the side of a triangle if given side and any two angles ( sine rule ) ( a ) : It says that c 2, the square of one side of the triangle, is equal to a 2 + b 2, the sum of the squares of the the other two sides, minus 2ab cos c, twice their product times the cosine of the opposite angle. Cosine is usually shortened to cos but is pronounced cosine. Relations between sides and angles of a triangle.
In the right triangle, the cosine function is defined as the ratio of the length of the adjacent side to that of the hypotenuse side.
\ [\text {area of a triangle} = \frac {1} {2} ab \sin {c}\] \ [5.45 = \frac {1} {2} \times 5.3 \times 3.2 \sin {c}\] \ [5.45 = 8.48 \sin {c}\] rearrange the equation to make. The longest side is the hypotenuse and the opposite side of the hypotenuse is the opposite side. As a consequence of the law of sine, we can neatly put a formula for the area of a triangle: Tan θ = sin θ/cos θ.
The cosine values of the most important angles can be obtained using the proportions of the.
Here are the formulas of sin, cos, and tan. The cosine is also equal to the sine of the complementary angle. The law of sines (or sine rule) is very useful for solving triangles: The formulas are given below:
Sina a = sinb b = sinc c.
Specifically, the sine is found by taking the side that is opposite the angle and dividing it by the hypotenuse of the triangle. This function can be used to determine the length of a side of a triangle when given at least one side of the triangle and one of the acute angles. Up to 10% cash back sin ( a ) = opposite side hypotenuse = h c sin ( a ) = h c ⇒ h = c sin ( a ) substituting the value of h in the formula for the area of a triangle, you get r =. Calculate the side of a triangle if given two other sides and the angle between them ( cosine rule) ( a ) :
A, b and c are angles.
Right triangle de nition assume that: (side a faces angle a, side b faces angle b and. Double angle formulas sin(2 ) = 2sin cos cos(2 ) = cos2 sin2 = 2cos2 1 = 1 2sin2 tan(2 ) = 2tan 1 tan2 degrees to radians formulas if x is an angle in degrees and t is an angle in radians then: Outside the triangle, the sine function can be used to find the y component of a vector that has any angle.
Tan θ = opposite side/adjacent side = bc/ab;
When the angle c is right, it becomes the pythagorean formula. Side of a triangle : Sine is the ratio of the opposite side to the hypotenuse side of the right triangle. = digit 1 2 4 6 10 f.
The three formulas of trigonometry are sine, cosine and tangent.
The sine angle formula is, \[\large sin\,\theta=\frac{opposite}{hypotenuse}\] solved examples Cos θ = adjacent side/hypotenuse side. In trigonometry, sin is the shorthand of sine function. It works for any triangle:
Cosine rule (the law of cosine):
The cosine of an angle is found by relating the sides of a right triangle. Cosine is a trigonometric ratio comparing two sides of a right triangle. As we remember from basic triangle area formula, we can calculate the area by multiplying triangle height and base and dividing the result by. Using trigonometry, we have sin (a) = h / c , and sin (c) = h / a.
Find the missing leg using trigonometric functions:
The sine is also equivalent to the cosine of the complementary angle. The basic relationship between the sine and the cosine is the pythagorean trigonometric identity: A = b * tan(α) b = a * tan(β) given area and one leg; Now as per sine, cosine and tangent formulas, we have here:
The three main trig ratios are sine, cosine and.
The cosine is equal to the length of the side adjacent to the angle divided by the length of the hypotenuse.