To find the area of a triangle, you’ll need to use the following formula: Area of a triangle formula. Using the formula, area of a triangle, a = 1/2 × b × h = 1/2 × 4 cm × 3 cm = 2 cm × 3 cm = 6 cm 2.
Area of Isosceles Triangle Formula, Examples, Definition
We agree to this nice of triangle pyramid volume formulas graphic could possibly be the most trending topic later than we allowance it in google benefit or facebook.
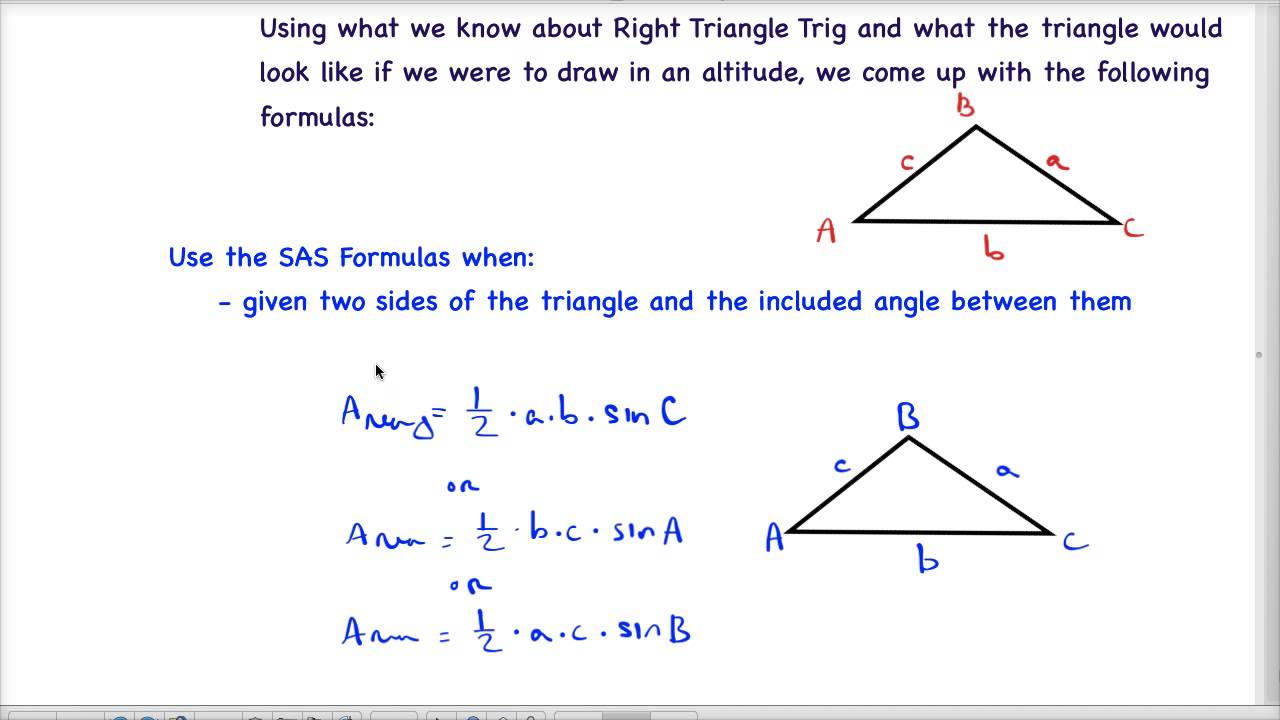
Area = 1 2 bc sin a.
The height is b × sin a. Find the area of the triangle. The area of a triangle with base, b, and height, h, is: \[\text{area of a triangle} = \frac{1}{2} ab \sin{c}\] to calculate the area of any triangle.
To find the area of the triangle on the left, substitute the base and the height into the formula for area.
The area of a triangle formula is: Heron’s formula for area of a triangle. The area of an equilateral triangle with side. A is the area, b is the base of the triangle (usually the bottom side), and h is the height (a straight perpendicular line drawn from the base to.
There are two important triangle formulas related to the area of a triangle, i.e., the herons formula and the pythagoras theorem.
Knowing how to find the height and area of a triangle with equal sides makes it so much easier to learn other. Base & height of a triangle are perpendicular to each other. The area of the triangle is equal to half of the product of the base and height of the triangle, it is given as, area of triangle, a = [(½) base × height] square units. To calculate the area of a triangle, multiply the height by the width (this is also known as the 'base') then divide by 2.
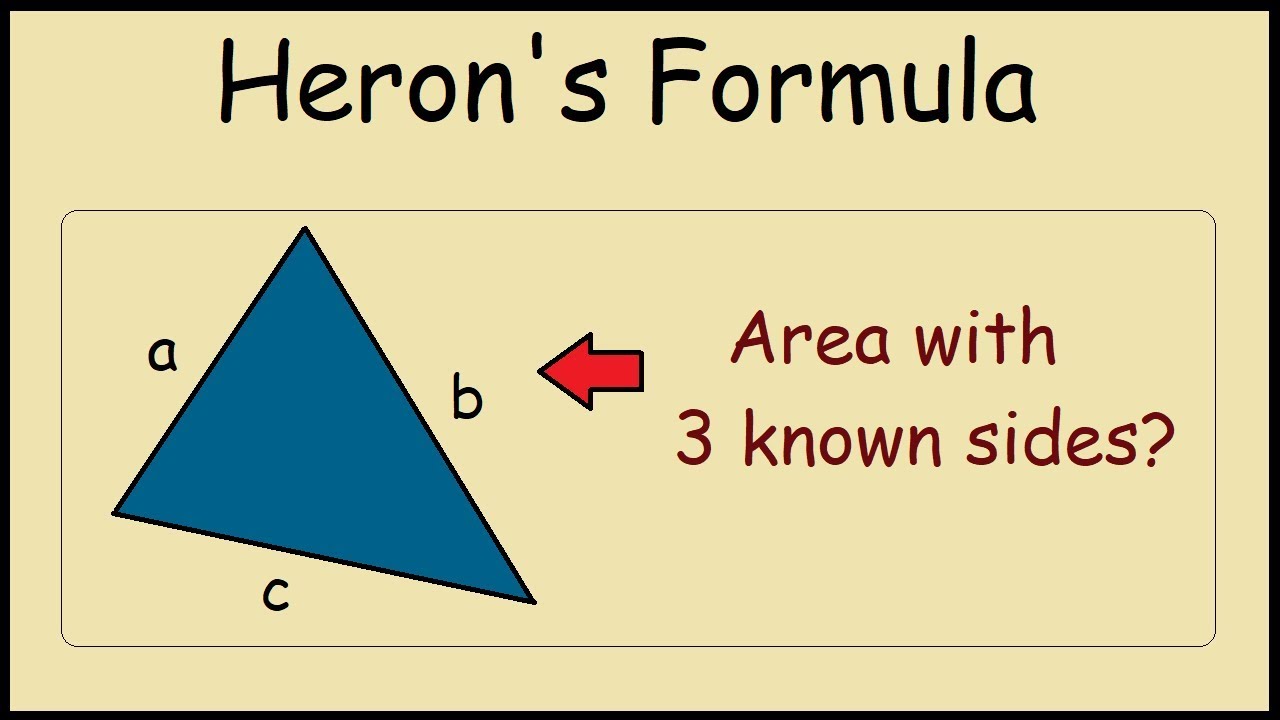
A method for calculating the area of a triangle when you know the lengths of all three sides.
Herons formula is a method for calculating the area of a triangle when the lengths of all three sides of the triangle are given. Where b and h are the base and height of the triangle, correspondingly. If the side lengths of the triangle are given, the area can be found using: The area of the triangle is:
Its submitted by admin in the best field.
Let me do the height in a different color. The area of a triangle formula = a = ½ (b × h) square units. Thus, the area of the triangle using heron's formula is 9.5, which is the same area we found in part (2). We know the base is c, and can work out the height:
Area = ½ × base × height.
Keep reading for solved examples So we know that the area of a triangle is going to be equal to one half times our base, times our height. So, the area a of a triangle is given by the formula a=12bh where b is the base and h is the height of the triangle. In geometry, a triangle is shape whose three sides are all the same length then it is.
Area=\( \sqrt{s(s−a)(s−b)(s−c)}\) where, s is half the perimeter, s= \( \frac{a+ b+ c}{2} \)
Apart from the above formula, we have heron’s formula to calculate the triangle’s area, when we know the length of its three sides. The formula for the area of the triangle can be expressed as area = a = ½ (b x h) square units, where h is the height of the triangle and b is the base of the triangle. Let a,b,c be the lengths of the sides of a triangle. This formula is applicable to all types of triangles.
The best known and the simplest formula, which almost everybody remembers from school is:
Area = ½ ab sin c. The general formula for the area of a triangle is equal to half the product of its height and base, i.e., a = 1/2 × b × h. Where b and h refer to the. Area = ½ × (c) × (b × sin a) which can be simplified to:
Area = 0.5 * b * h, where b is the length of the base of the triangle, and h is the height/altitude of the triangle.
The area is given by: The area of any triangle can be calculated using the formula: A triangle is one of the most basic shapes in geometry. Then, you can use the formula a = √3/4 (a²) to determine the area of an equilateral triangle.
You can use the pythagorean theorem and height of the right triangles within the equilateral to determine the missing side lengths of an equilateral triangle.
Find the area of a triangle where height = 5 cm and width = 8 cm. Similarly, what are the formulas for triangles? The formula to find the area of a right triangle is given by: {eq}area\ =\ \frac{1}{2}\cdot base\cdot height {/eq} area of a right triangle
$$ area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (12.
Let a, b, c are the lengths of the sides of a triangle. Where a, b, and c are side lengths, and. The area of a circle with radius r is: Part (3c) here we are asked to find the area of the triangle using the law of sines.
The area of a right triangle is the region covered by its boundaries or within its three sides.
Area of a right triangle = 1 2bh a r e a o f a r i g h t t r i a n g l e = 1 2 b h. By changing the labels on the triangle we can also get: