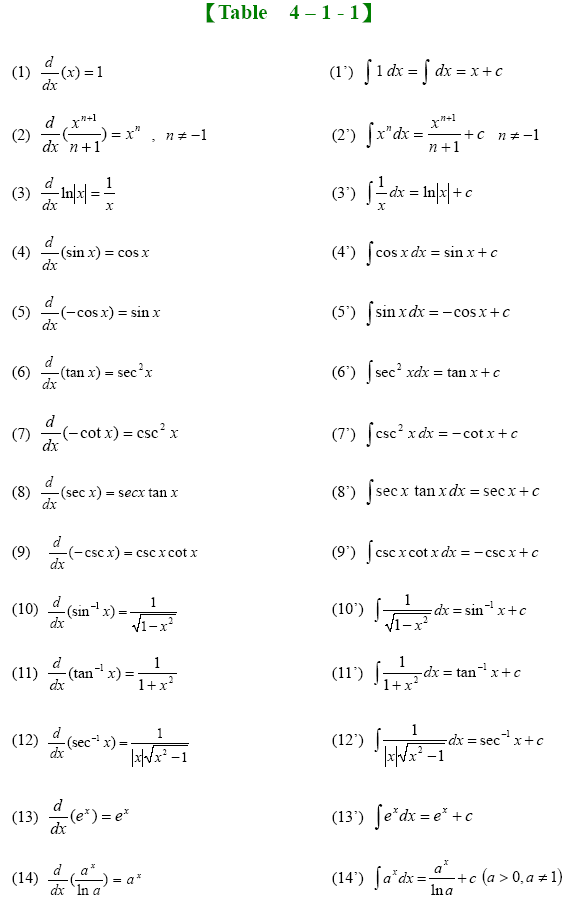In the first two integrals, x and y are dummy variables and so any label may be chosen for them. Z xn dx= xn+1 n+1 +c (n6= 1) 2. Using the standard integrals is straight forward when the question is already in standard form:
2.1.11.12.4 Chapter 4 Indefinite Integrals
A table of integrals f(x) r f(x)dx k, any constant kx+c x x2 2 +c x2 x3 3 +c
If a term in your choice for yp happens to be a solution of the homogeneous ode corresponding to (4), multiply this term by x (or by x 2 if this solution corresponds to a double root of the
Z dx a 2+x = 1 a tan 1 x a +c 9. Integral, (( )) ( ) ( ) ( ) b gb( ) a ga ∫∫f g x g x dx f u du′ =. Z dx x = lnjxj+c 3. An+1 0 ∞ ∫ integration by parts:
The product of two integrals can be expressed as a double integral:
E x dx = e x + c. Table of useful integrals, etc. Foundon the internet (e.g., table of conformalmappings); Integration by parts the standard formulas for integration by parts are, bb b aa a ∫∫ ∫ ∫udv uv vdu=−= udv uv vdu− choose uand then compute and dv du by differentiating u and compute v by using the fact that v dv=∫.
Get this from a library!
Z secxdx= ln secx+tanx +c 12. Basic forms z xndx = 1 n +1 xn+1(1) z 1 x dx =ln|x| (2) z udv = uv z vdu (3) z 1 ax + b dx = 1 a ln|ax + b| (4) integrals of rational functions z 1 (x + a)2. Table of integrals basic forms (1)!xndx= 1 n+1 xn+1 (2) 1 x!dx=lnx (3)!udv=uv!vdu (4) u(x)v!(x)dx=u(x)v(x)#v(x)u!(x)dx rational functions (5) 1 ax+b!dx= 1 a ln(ax+b) (6) 1 (x+a)2!dx= 1 x+a (7)!(x+a)ndx=(x+a)n a 1+n + x 1+n #$ % &', n!1 (8)!x(x+a)ndx= (x+a)1+n(nx+xa) (n+2)(n+1) (9) dx!1+x2 =tan1x (10) dx!a2+x2 = 1 a tan1(x/a) (11) xdx!a2+x2. After a bit of manipulation these integrals can be put into standard form and their.
Sometimes restrictions need to be placed on the values of some of the variables.
Table of standard integrals 1. Z e xdx= e +c 4. In addition, the methods that are used to solve these integrals will apply to similar integrals, so it is worth knowing. Z tanxdx= ln cosx +c 7.
More compact collections can be found in e.g.
Standard specifications for public works construction sponsored and distributed by: Also, get the downloadable pdf of integral formulas for different functions like trigonometric function, rational functions, etc. Basic forms z xndx = 1 n+ 1 xn+1(1) z 1 x dx= lnjxj (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2. Udv a b ∫=#uv$% a b −vdu a b ∫ u and v are functions of x.
I2 = z ∞ −∞ z ∞ −∞ e−(x2+y2) dxdy the differential dxdy represents an elementof area in cartesian
Z cosec2 xdx= cotx+c 11. Table of integrals engineers usually refer to a table of integrals when performing calculations involving integration. This area of algebraic combinatorics has been rapidly developed during the last decade. The integral by i, we can write i2 = µz ∞ −∞ e−x2 dx ¶ 2 = z ∞ −∞ e−x2 dx ∞ −∞ e−y2 dy (2) where the dummy variable y has been substituted for x in the last integral.
Table of basic integrals basic forms (1) z xndx= 1 n+ 1 xn+1;
Brychkov, marichev, prudnikov's tables of indefinite integrals, or as chapters in zwillinger's crc standard mathematical tables and formulae or bronshtein and semendyayev's guide book to mathematics, handbook of mathematics or users' guide to mathematics, and other mathematical handbooks. B x dx = b x / ln (b) + c. •informationdifficult to find on the internet due to the challenges of entering an appropriatequery (e.g., integral tables). E−ax2dx= 1 2 π a # $% & ’(1 2 0 ∞ ∫ ax xe−2dx= 1 2a 0 ∞ ∫ x2e−ax2dx= 1 4a π a # $% & ’(1 2 0 ∞ ∫ x3e−ax2dx= 1 2a2 0 ∞ ∫ x2ne−ax2dx= 1⋅3⋅5⋅⋅⋅(2n−1) 2n+1an π a $ %& ’ 1 2 0 ∞ ∫ x2n+1e−ax2dx= n!
Integral formulas are listed along with the classification based on the types of functions involved.
Regional transportation commission of washoe county carson city churchill county city of reno city of sparks city of yerington washoe county revision no. This leaflet provides such a table. Table 2.1, choose yp in the same line and determine its undetermined coefficients by substituting yp and its derivatives into (4). Dx= 1 x+ a (5) z (x+ a)ndx= (x+ a)n+1.
2an+1 0 ∞ ∫ xne−axdx= n!
The fundamental theorem of calculus establishes the relationship between indefinite and definite. Z cotxdx= ln sinx +c 8. The angular integration yields a factor of /2, and the radial integral is just g(1) Z cosecxdx= ln cosecx cotx +c 13.
Basic forms z xndx= 1 n+ 1 xn+1(1) z 1 x dx= lnx (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2.
N6= 1 (2) z 1 x dx= lnjxj (3) z udv= uv z vdu (4) z 1 ax+ b dx= 1 a lnjax+ bj integrals of rational functions (5) z 1 (x+ a)2 dx= 1 x+ a (6) z (x+ a)ndx= (x+ a)n+1 n+ 1;n6= 1 (7) z x(x+ a)ndx= (x+ a)n+1((n+ 1)x a) (n+ 1)(n+ 2) (8) z 1 1 + x2 dx= tan 1 x (9) z 1 a2 + x2 dx= 1 a tan 1 x a 1 Std normal table.xls created date: These restrictions are shown in the third column.