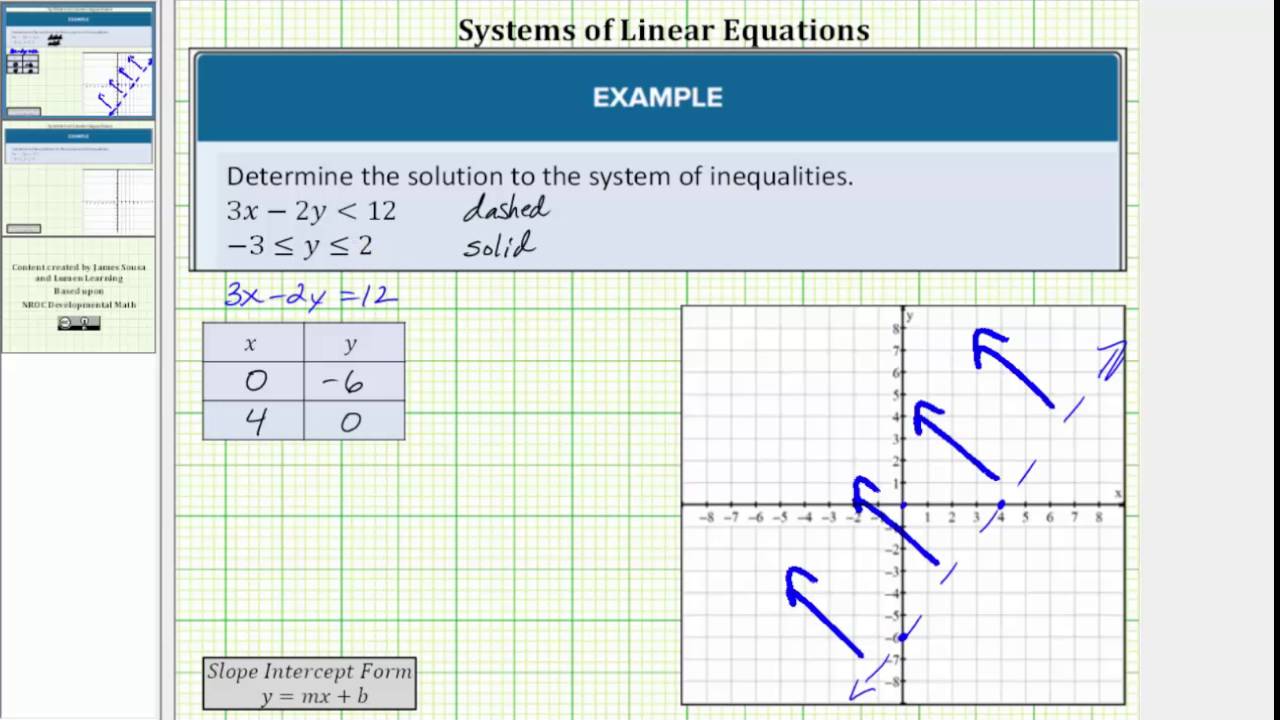
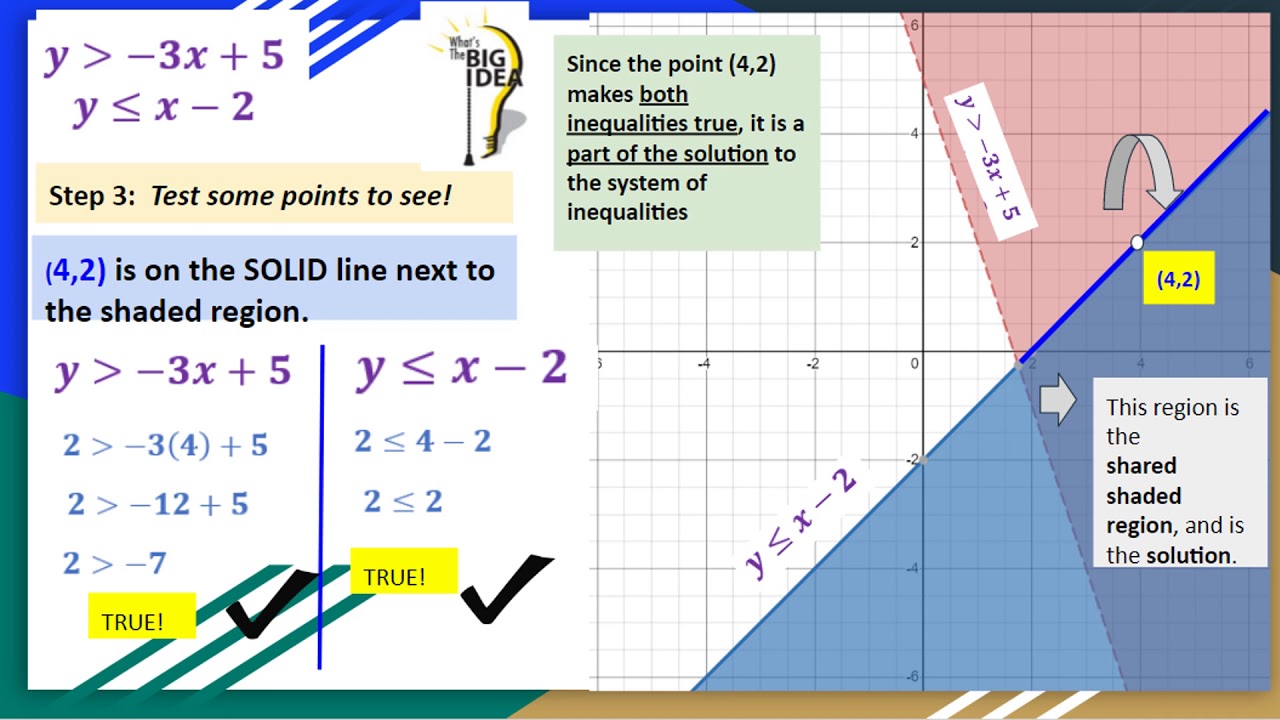
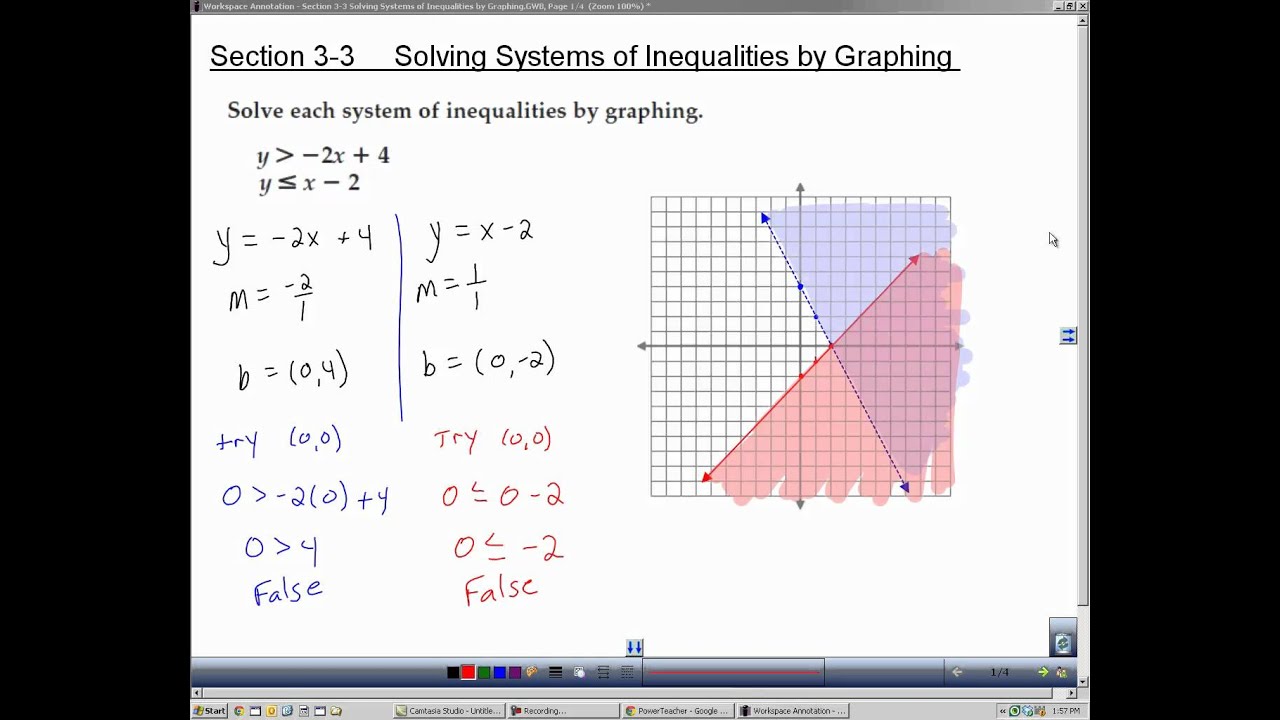
The vertices occur at the points of intersection of the corresponding equation of the given system of inequalities. Solution set of the system of inequalities definition the combination of two or more than two inequalities having one or more than two independent variable is known as the system of inequalities. All points in the area where the shaded regions overlap are solutions to both inequalities in the system.
📈Which system of linear inequalities has the point (2, 1
− 1 3x − y ≤ 3 − 1 3(− 3) − (3) ≤ 3 1 − 3 ≤ 3 − 2 ≤ 3.
The solution set of the given system of inequalities is the intersection of the solutions of each of the given inequality.
We can choose either x or y in either the first or second equation. The solution is any ordered pair that satisfies each of the inequalities. Sometimes making a table of values makes sense for more complicated inequalities. Sometimes it is necessary to find the common solution, or solution set, of two or more inequalities, called a system of inequalities.
To graph a system of linear inequalities.
Dividing both sides by 2, x ≤ 2 X 25y x + 5y s 4 d. Solve 2x + 3 ≤ 7, where x is a natural number. (−3, 3) is not a solution;
Created by sal khan and monterey institute for technology and education.
Step 2 substitute the value of x into the other equation. A < 5) and not for exact numbers (e.g. (10 , 10) or (5, 8) 14) write a system of inequalities whose solution is the set of all points in quadrant i not including the axes. 13) state one solution to the system y < 2x − 1 y ≥ 10 − x many solutions.
Then consider the related equation obtained by changing the inequality sign to an equality sign.
Y = 9 − x 2. To solve the system of inequalities, we can repeat this graphing process for the other inequality, y ≥ x. Since you only solve for ranges in inequalities (e.g. Has a line by 2 and 3.
Which system of linear inequalities is represented by the graph?
Subtracting 3 from both the sides, 2x ≤ 4. This system of inequalities has a set of solutions that satisfies all the equations comes out from the inequalities by replacing the inequality sign with the equal sign. Please, see the attached graph. Makes the inequality 3x+2y≤6 3 x + 2 y ≤ 6 a true statement.
( − 3, 3) inequality 1:
The solution set of the given system of inequalities is the intersection of the solutions of each of the given inequality. If the inequality is strict ( < or > ), graph a dashed line. The intersection of the solutions of each inequality is the solution of the system of inequalities. 1) you can only use the elimination method, not the substitution method.
It means, each and every value in the solution set will satisfy the inequality and no other value will satisfy the inequality.
Which system of linear inequalities is represented by the graph? 2x + 3 ≤ 7. Free trial available at kutasoftware.com Let us find the solution of the following system of inequalities.
The graph of this equation is a line.
(3) y = x + 3. The solution to the system is the area where the shaded portions of the graphs overlap. Sal graphs the solution set of the system y≥2x+1 and y1.. In this case the equation is 2x + 3y = 1.
To graph a linear inequality in two variables (say, x and y ), first get y alone on one side.
Therefore, the solution set is shown as shaded region. A solution set is the set of values which satisfy a given inequality. By using this website, you agree to our cookie policy. The solution set of inequality x > 3 is the set of all the real numbers greater than 3.
2x + 6y ≤ 6 2(− 3) + 6(3) ≤ 6 − 6 + 18 ≤ 6 12 ≤ 6.
Y ≤ 2x + 1 Up to 10% cash back explanation: The solution set of a system of inequality is thus the intersection of the solution set of each inequality in the system. Example find the solution set of the following system:
It does not satisfy both inequalities.
Therefore, the solution set is shown as shaded region. Systems of inequalities can be solved just like systems of equations, but with three important caveats: Substitute the coordinates of ( x, y) = (−3, 3) into both inequalities. Y \geq x y ≥ x.
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded.
Step 1 we must solve for one unknown in one equation.