The separation of concentration and time terms (this time keeping the negative sign on the left for convenience) yields. The rate can be written as. By elementary integration of these differential equations integrated rate laws can be obtained:
Integrated Rate Law Second Order YouTube
Putting the limits in equation (1) we get the value of c, ⇒ [ a] 0 = c.
A chemist calls them second order rate laws because the rate is proportional to the product of two concentrations.
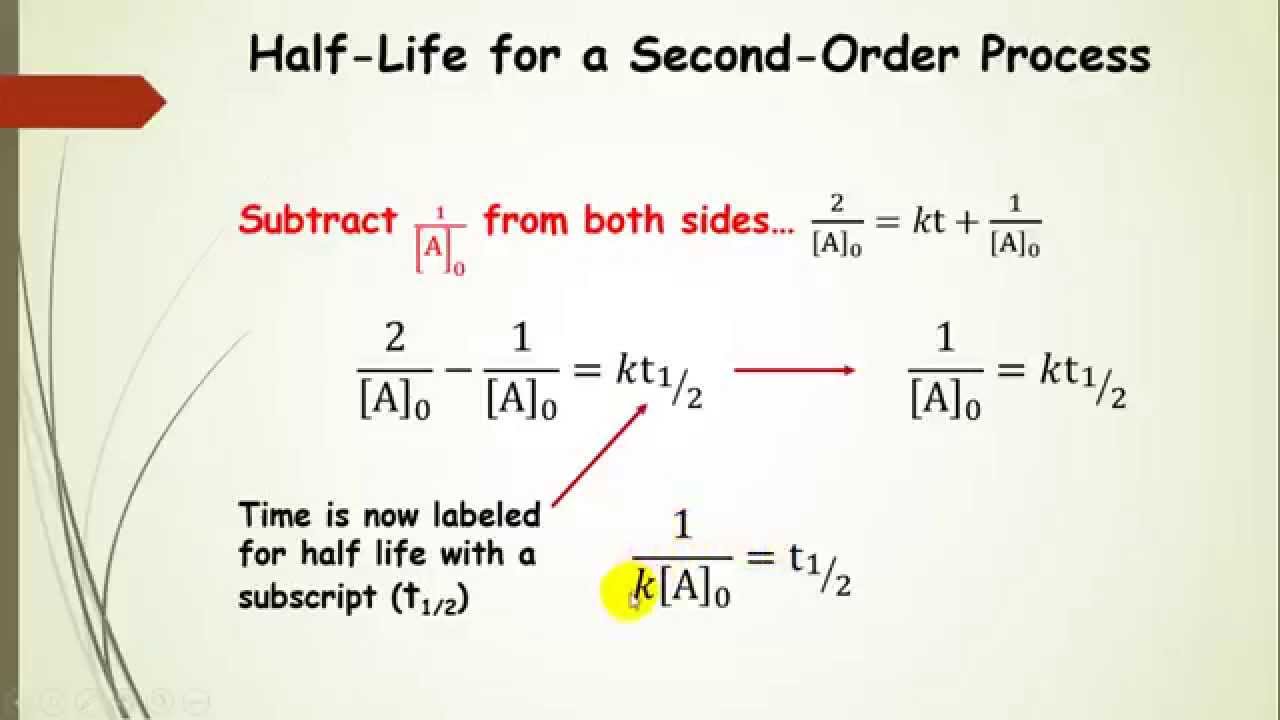
The equation for the second order integrated rate law takes the form y = mx +b, where y = 1/a; When a reaction is of second order with regard to a specific reactant, an increase in its quantity causes the rate to grow. The second order integrated rate law is {eq}1/[a]_t = kt + 1/[a]_0 {/eq}. 1 [ a ] vs.
1 [ a ] = k t + ( 1 [ a ] 0 ) 1 [ a ] = k t + ( 1 [ a ] 0 ) plot needed for linear fit of rate data [a] vs.
− d [ r] d t = k [ r] 2. (11.6.1) − d [ a] d t = k [ a] 2. Considering the scenario where one second order reactant forms a given product in a chemical reaction, the differential rate law equation can be written as follows: These are inherently differential equations, because the rate is always defined as a change in concentration with time;
Integrated rate law [ a ] = − k t + [ a ] 0 [ a ] = − k t + [ a ] 0.
(1) where, c= constant of integration, at time, t=0, [a] = [ a] 0. Thus, the graph of the second order integrated rate law is a straight. In order to obtain the integrated rate equation, this differential form must be rearranged as follows: For the reaction given by 2no + o 2 → 2no 2, the rate equation is:
2a products or a + b products (when [a] = [b]) , rate = k[a] 2 the integrated rate law is 1/[a] = kt + 1/[a o ]
The overall order of the reaction = sum of exponents of reactants in the rate. In mathematical language, these are first order differential equations because they contain the first derivative and no higher derivatives. The integral form of the equation was obtained from the differential form and the full integration can be found here. 1 [a]t = kt+ 1 [a]0 y = mx+b 1 [ a] t = k t + 1 [ a] 0 y = m x + b.
Because this equation has the form y = mx + b, a plot of the inverse of [a] as a function of time yields a straight line.
The rate constant for the reaction can be determined from the slope of the line, which is equal to k. If the plot is not a straight line, then the reaction is not second order. (11.6.2) − d [ a] [ a] 2 = k d t. Rate = k[no] 2 [o 2] find the overall order of the reaction and the units of the rate constant.
−d[r] /dt = k[r] 2;