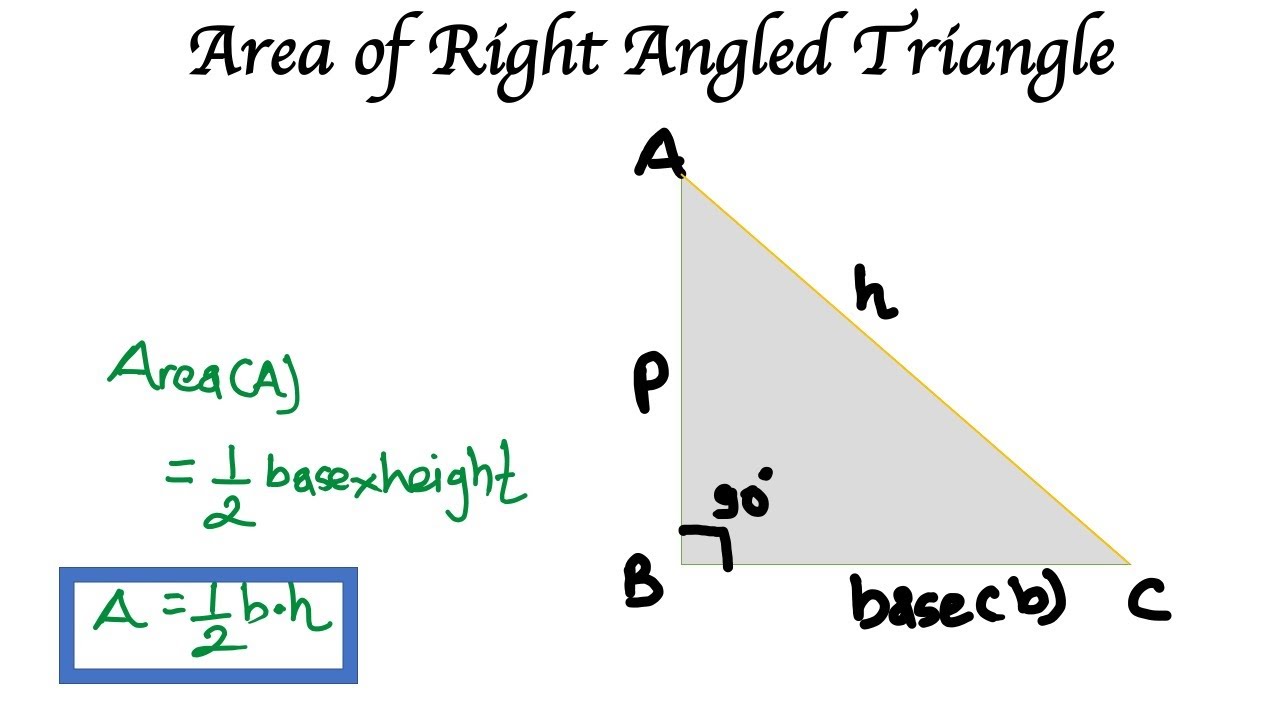
A = ½ × a 2. As we remember from basic triangle area formula, we can calculate the area by multiplying triangle height and base and dividing the result by two. Since multiplying these to values together would give the area of the corresponding rectangle, and the triangle is half of that, the formula is:
PPT Shape and Space PowerPoint Presentation, free
The area of a triangle is given by the equation:
In a right triangle, the base and the height are the two sides which form the right angle.
Since the base leg of the given. A² + b² = c² Because the right triangle legs are perpendicular to each other, one leg is taken as a base and the other is a right triangle height: Let's create a right triangle, △ c as △ c a s, with ∠a ∠ a as the right angle.
Now that we know our base and height, we can simply plug these numbers into the area of a right triangle formula:
A = [c 2 ×sin (β)×sin (α)/ 2×sin (2π−α−β)] area formula for an isosceles right triangle. Up to 10% cash back 12 square centimeters. P = \frac {a \cdot b}{2} How to find the area of a right triangle area of a right triangle (formula & examples).
Area of right triangle formula.
Area = = a² * sin(β) * sin(γ) / (2 * sin(β + γ)) if you are looking for other formulas or calculators connected with triangle, check out this right triangle calculator, pythagorean theorem calculator and law of cosines calculator. Derivation of the area formula S = semi perimeter of the triangle having this formula s = (a + b + c) / 2. How to calculate area of right triangle using right triangle formula when its perimeter, height, and base are given?
\(a = \frac{1}{2} b \times p\).
Therefore, the height of the triangle will be the length of the perpendicular side. Area of a right triangle = a = ½ × base × height (perpendicular distance) from the above figure, area of triangle acb = 1/2 ab Put the values of height h and base b in the area formula, (1/2)bh In a right triangle, if one leg is taken as the base then the other is height, so the area of a right triangle is one half the product of the two legs.
It measures 90° 90 °.
Area = a * b / 2. Calculate the area of the triangle pictured below. In an isosceles right triangle, hypotenuse is given by formula h=b \(\sqrt{2}\), the area is given by b 2 /2, and perimeter is given by 2b+h. Where b is the length of the triangle’s base and h is the length of the height.
Area and perimeter of a right triangle are calculated in the same way as any other triangle.
Given area and one leg; $$ area = \frac {1} {2} (base \cdot height) \\ =\frac {1} {2} (24 \cdot 27.6) \\ = 331.2 \text { inches squared} $$. The formula to calculate the area of a right triangle is given by: The formula for the area of a right triangle is given by:
Area = a * b / 2
Check for the given values. Area of right triangle formulas the simplest formula for calculating the area of this triangle is to multiply the value of the legs and divide them by two: Perimeter = a + b + c All that you need are the lengths of the base and the height.
A = ½ [√ (a 2 − b 2 ⁄4) × b] using the length of 2 sides and an angle between them.
The area of a right triangle can be calculated by using the following formula: This next sample problem is a bit trickier than the other two. If you have one leg and hypotenuse given, use the pythagorean theorem to find the missing leg: As a formula the area t is.
The area of the equilateral triangle is √3/4 x a².
The perimeter is the sum of the three sides of the triangle and the area can be determined using the following equation: The perimeter of a right triangle:s = a + b + c. A right triangle is a special case of a scalene triangle, in which one leg is the height when the second leg is the base, so the equation gets simplified to: Area of a right triangle:
$a=1/2bh$ $a=1/2(5)(5)$ $a=12.5$ the area of this triangle is 12.5 square units.
Where, “b” is the base (adjacent side) “h” is the height (perpendicular side) hence, the area of the right triangle is the product of base and height and then divide the product by 2. The right triangle comes along frequently in geometry. Area = (1/2)base * height. Where b and p are the base and height of the triangle respectively.
T = 1 2 a b {\displaystyle t= {\tfrac {1} {2}}ab} where a and b are the legs of the triangle.
Area of right triangle, a = (½) × b × h square units. To find the area of the triangle on the left, substitute the base and the height into the formula for area.