Area = 30 in 2. Your final answer must be given in units 2 (e.g. Area = (1/2)base * height.
Area of Right Triangle Worksheets
By changing the labels on the triangle we can also get:
Up to 10% cash back 24 square centimeters.
Area = a² / 2 Since the base leg of the given. Cm 2, m 2, mm 2 ). The sum of angles in the triangle is 180°, with α + β = 90°.;
For example, if we know only the right triangle area and the length of the leg a, we can derive the equation for other sides:
Area = ½ ca sin b; A,b and c are the sides of the triangle. This can be shortened to. Area = ½ × base × height.
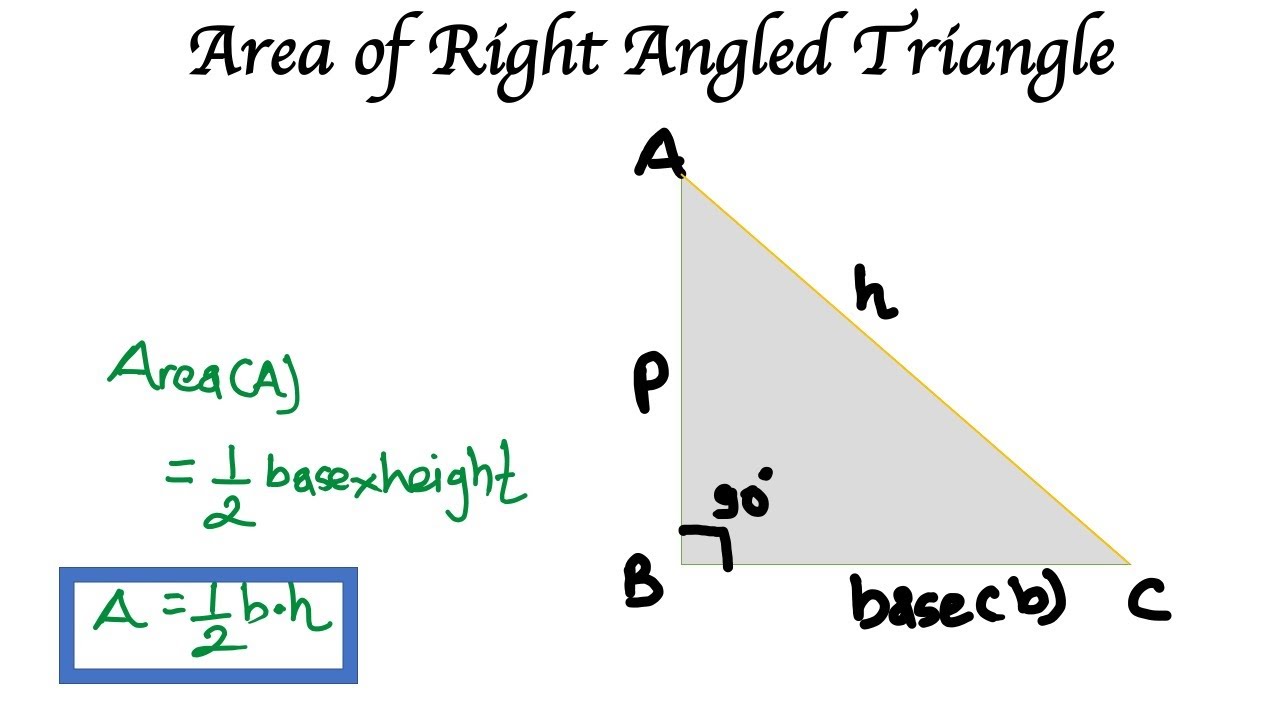
In a right triangle, the base and the height are the two sides which form the right angle.
Therefore, the height of the triangle will be the length of the perpendicular side. We can calculate the area of the right angle triangle using the. S = semi perimeter of the triangle having this formula s = (a + b + c) / 2. Since multiplying these to values together would give the area of the corresponding rectangle, and the triangle is half of that, the formula is:
The other two are called legs or catheti.
Perimeter = a + b + c. A right triangle is a special case of a scalene triangle, in which one leg is the height when the second leg is the base, so the equation gets simplified to: Area of right triangle, a = (½) × b × h square units. Area = ½ × (c) × (b × sin a) which can be simplified to:
Sin (b) = b/c, cos (b) = a/c, tan (b) = b/a.
Using the area of a triangle formula, area = (1/2) × b × h. Area of a triangle = base × height 2 area of a triangle = base × height 2. Solved examples on area of right angle triangle. Where, “b” is the base (adjacent side) “h” is the height (perpendicular side) hence, the area of the right triangle is the product of base and height and then divide the product by 2.
Area = (1/2) × 5 × 12.
The area of a right triangle can be found using the formula a = ½ bh. A = 1 2bh a = 1 2 b h. Where, s is the semi perimeter and is calculated as $$ s = {{(a + b + c)} \over 2}$$ and a, b, c are the sides of a triangle. Where b is the base length and h is the height of the triangle.
In an isosceles right triangle, hypotenuse is given by formula h=b √2 2, the area is given by b 2 /2, and perimeter is given by 2b+h.
So the area of an isosceles right triangle is: We start with this formula: The area of a triangle is given by the equation: Area = a*b/2, where a is height and b is base of the right triangle.
Area = a * b / 2.
The perimeter is the sum of the three sides of the triangle and the area can be determined using the following equation: In such triangle the legs are equal in length (as a hypotenuse always must be the longest of the right triangle sides): We know the base is c, and can work out the height: Base = √25 = 5 in.
The formula for the area of a right triangle is given by:
Area of a right angled triangle. Area of a right triangle = a = ½ × base × height (perpendicular distance) from the above figure, B = 2 * area / a; Height = 12 in, hypotenuse = 13 in.
Area = ½ ab sin c;
Area and perimeter of a right triangle are calculated in the same way as any other triangle. The formula to calculate the area of a right triangle is given by: Isosceles right triangle is a two dimensional three sided figure in which one angle measures 90°, and the other two angles measure 45° each. Area = 12 bc sin a.
Edge lengths can be determined using the pythagoras theorem, angle sizes using the trigonometric functions.
Area of right triangle formula. The height is b × sin a. The area of any other triangle can be found with the formula below. The right angled triangle formula is given by (hypotenuse) 2 = (adjacent side) 2 + (opposite side) 2 = (20) 2 + (15) 2 = 400 + 225 = 625 cm hypotenuse =
Area of a right angled triangle formula.
This formula works for a right triangle as well, since the since of 90 is one. The longest side of the right angle triangle is its hypotenuse. The formula for area of a right triangle is given by: