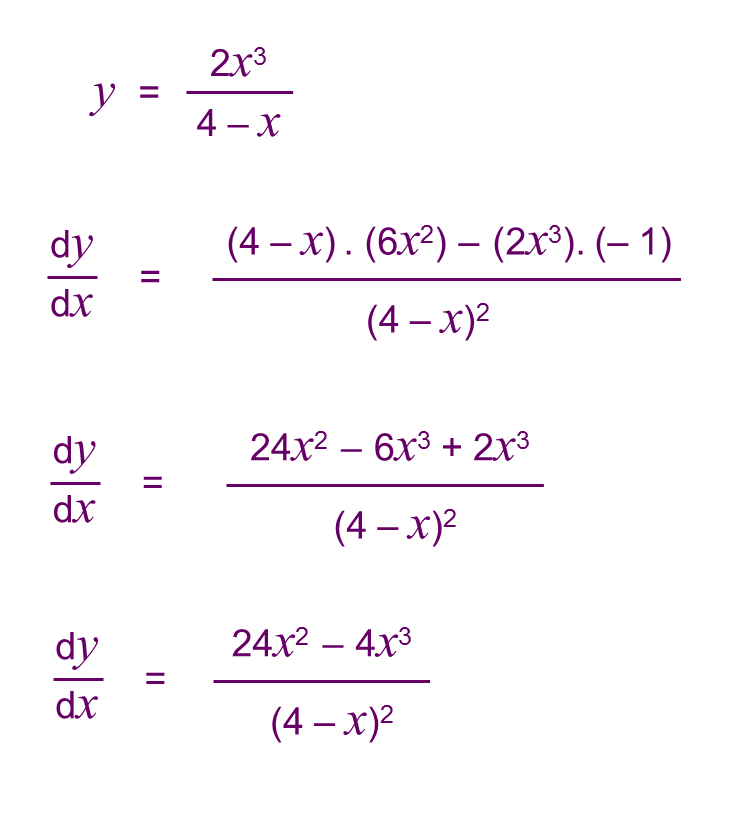This requires a differentiation only, no extra integration. We present the quotient rule version of integration by parts and demonstrate its use. The constant multiple rule click to select your answer.
Pdf of integration by part
Then sin(x−1/2) x2 dx = 2cos(x−1/2) x1/2 + 2cos(x−1/2) x · 1 2 x−1/2 dx = 2cos(x−1/2) x1/2 −2 cos(x−1/2)· −
A quotient rule integration by parts formula, apply the resulting integration formula to an example, and discuss reasons why this formula does not appear in calculus texts.
Let u = x1/2, dv = sin(x−1/2) x3/2 dx, du = 1 2 x−1/2 dx,v= 2cos(x−1/2). 1529 eighteenth street nw, washington, dc 20036. In calculus, the quotient rule is a method for determining the derivative (differentiation) of a function in the form of the ratio of two differentiable functions. Integration by parts is used to integrate the product of two or more functions.
∫ a b f ( y) d x.
The product rule ° c, the quotient rule o d. The first one is that you can apply limits after the end of your integrating result as you did in indefinite integration but make sure your variable is the same. We will apply the limit definition of the derivative: Rules for solving integration by parts for definite integral limits.
| find, read and cite all.
We obtain a quotient rule integration by parts formula: In conventional integration by parts, however, once u and dvare chosen, both a differentiation and an integration This rule is also called the antiderivative quotient or division rule. From the integration by parts formula discussed above, u is the function u(x) v is the function v(x)
Let f and g be differentiable at x with g ( x) ≠ 0.
Letting u = g (x) and v = f (x) and observing that du = g (x) dx and dv = f (x) dx, we obtain a quotient rule integration by parts formula: 10 pls on which derivative rule is integration by parts based? Quotient rule in integration is known as integration by parts. (2) uu u2 as an application of the quotient rule integration by parts formula, consider theintegral sin (x −1/2) dx.
Integration by parts can be extended to functions of several variables by applying a version of the fundamental theorem of calculus to an appropriate product rule.
Let’s take an example of. Then f / g is differentiable at x and. The formula for the integral division rule is deduced from the integration by parts u/v formula. The two functions to be integrated f (x) and g (x) are of the form ∫ f ( x ).
[ f ( x) g ( x)] ′ = g ( x) f ′ ( x) − f ( x) g ′ ( x) [ g ( x)] 2.
By the quotient rule, if f (x) and g(x) are differentiable functions, then d integrating both sides of this equation, we get f that is, f(x) which may be rearranged to obtain f___ \int _ { a } ^ { b } f ( y ) dx ∫. (2) as an application of the quotient rule integration by parts formula, consider the integral sin(x−1/2) x2 dx. It is also known as antiderivative quotient or division rule.
The integral quotient rule is the way of integrating two functions given in form of numerator and denominator.
Select rating give a quotient rule integration by parts formula 1/5 give a quotient rule integration by parts formula 2/5 give a quotient rule integration by parts formula 3/5 give a quotient rule integration by parts formula 4/5 give a quotient rule integration by parts formula 5/5. X2let u = x 1/2, dv = sin (x −1/2) dx, du = 1 x−1/2 d x, x 3/2 2 v = 2 cos (x−1/2).then sin (x −1/2) 2 cos. Dv u = v u + v u2 du. Calculus , mathematical concepts , mathematical applications , college mathematics mathematical association of america.
Proof of the product rule and quotient rule using difference quotient methods and implicit differentiation and logarithms.
1) on which derivative rule is the method of integration by parts based? F ′ ( x) = lim δ x → 0 f ( x + δ x) − f ( x) δ x. Select the correct answer below. The quotient rule follows the definition of the limit of the derivative.
H ′ ( x) = [ f ( x) g.
Integration by parts, definite integrals. By using this website, you agree to our cookie policy. Letting u = g (x) and v = f (x) and observing that du = g (x) d x and dv = f (x) d x,we obtain a quotient rule integration by parts formula: Proof of integration by parts usi.
Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point.
3) determine whether the following statements are true. It is a formal rule used in the differentiation problems in which one function is divided by the other function. The power rule 0 e, the constant rule o f. If it is true, give a brief explanation.
To calculate the integration by parts, take f as the first function and g as the second function, then this formula may be pronounced as: