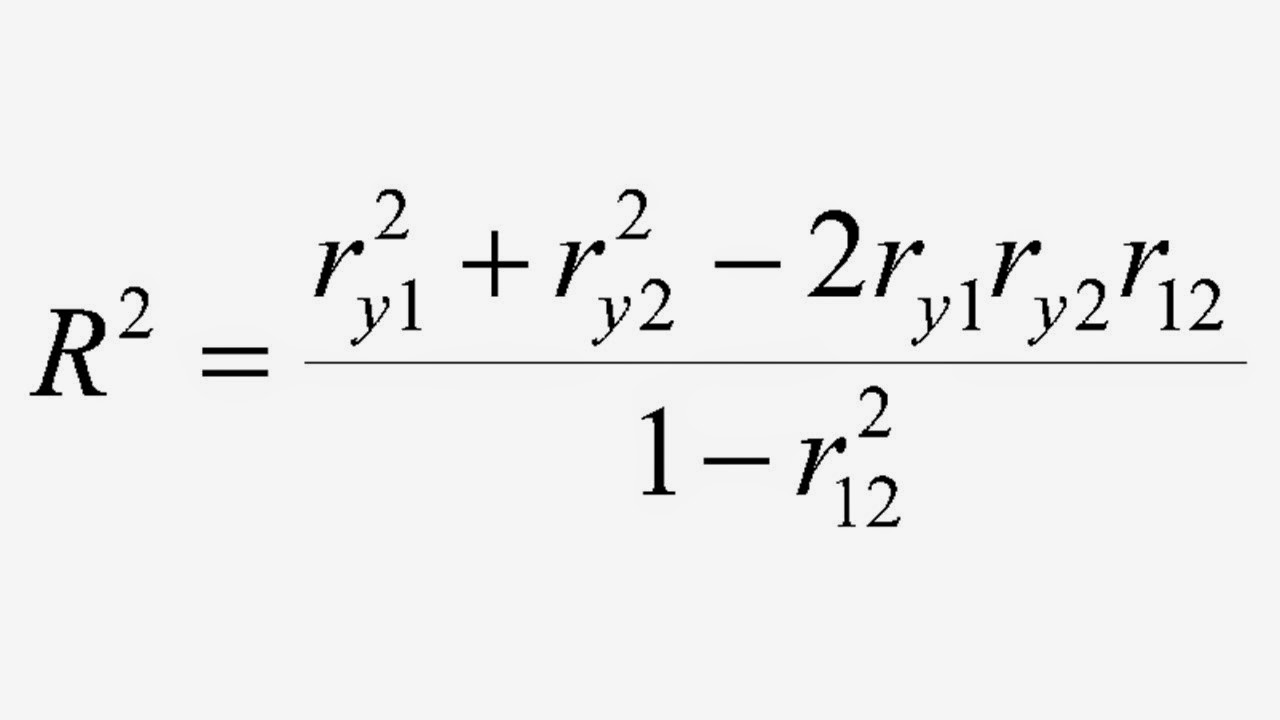The subscript j indicates the predictors and each predictor has one vif. In regression analysis, when this assumption is violated, the problem of multicollinearity occurs. Treasury note yield, merrill lynch u.s.
Multiple Linear Regrssion Chapter3.3 Multicollinearity
Vif, tolerance indices (tis), and correlation coefficients are useful metrics for multicollinearity detection.
The smallest possible value of vif is 1.0, indicating a complete absence of multicollinearity.
The formula for vif is very simple and hence. Perfect (or exact) multicollinearity if two or more independent variables have an exact linear relationship between them then Likewise, a vif of 100 corresponds to an rsquare of 0.99. This is an extension of the simple case of collinearity between two variables.
Variables are said to be multicollinear if there is a linear relationship between them.
For example, we can calculate the vif for the variable points by performing a multiple linear regression using points as the response variable and assists and rebounds as the explanatory variables. Its value lies between 0 and 1. So more precisely, vifs use a multiple regression model to calculate the degree of multicollinearity. In this situation, the coefficient estimates of the multiple regression may change erratically in response to small changes in the model or the data.
Treasury bill yield, 10 years u.s.
When we are checking for multicollinearity, we should check multiple indicators and look for patterns among them. Looking at correlations only among pairs of predictors, however, is limiting. The end objective) that is measured in mathematical or statistical or financial modeling. Hence, greater vif denotes greater correlation.
A vif for a predictor of 10.0 corresponds to an rsquare value of 0.90.
Demonstrate a linear relationship between them. If the degree of correlation is high enough between variables, it can cause problems when fitting and interpreting the regression model. This correlation is a problem because independent variables should be independent.if the degree of correlation between variables is high enough, it can cause problems when you fit the model and interpret the results. For example, for three variables x1, x2 and x3, we say that they are multicollinear if we can write:
Multicollinearity in regression analysis occurs when two or more predictor variables are highly correlated to each other, such that they do not provide unique or independent information in the regression model.
High yield corporate bond index yield effective monthly yields, u.s. Generally, a vif above 5 indicates a high multicollinearity. Variance inflation factor and multicollinearity. In ordinary least square (ols) regression analysis, multicollinearity exists when two or more of the independent variables independent variable an independent variable is an input, assumption, or driver that is changed in order to assess its impact on a dependent variable (the outcome).
Multicollinearity occurs when independent variables in a regression model are correlated.
Where a and b are real numbers. That's why many regression analysts often rely on what are called variance inflation factors ( vif) to help detect multicollinearity. They should all be high. Multicollinearity diagnosis using variance inflation factor (vif) permalink.
When r 2 i r i 2 = 0, there is a complete absence of multicollinearity, but when r 2 i r i 2 = 1, there is exact multicollinearity.
This can be done by placing the formula =randbetween(1,40) in range c1:e10. Exact collinearity is a perfect linear relationship between two explanatory variables x 1 and x 2.in other words, exact collinearity occurs if one variable determines the other variable (e.g., x 1 = 100 − 2x 2).if such relationship exists between more than two explanatory variables (e.g., x 1 = 100 − 2x 2 + 3x 3), the relationship is defined as. Multicollinearity page 1 of 10 perfect multicollinearity is the violation of assumption 6 (no explanatory variable is a perfect linear function of any other explanatory variables). Structural multicollinearity is a mathematical artifact caused by creating new predictors from other predictors — such as creating the predictor x 2 from the predictor x.
It describes a perfect or exact relationship between the regression exploratory variables.
Read more in the equation predict the perfect linear relationship. The term multicollinearity was first used by ragnar frisch. Multicollinearity means independent variables in a model are correlated. It is possible that the pairwise correlations are small, and yet a linear dependence exists among three or even more variables, for example, if x3 = 2 x1 + 5 x2 + error, say.
Multicollinearity is an interesting problem to solve.
S&p 500® index replicating etf (ticker symbol: X1 = ax2 + bx3. This produces the following output: Now run the regression and see what the vif values are.
Create near collinearity between x1 and x3 and between x2 and x4.
Spy) adjusted close prices arithmetic monthly returns, 1 year u.s. Linear regression analysis assumes that there is no perfect exact relationship among exploratory variables. In statistics, multicollinearity (also collinearity) is a phenomenon in which one predictor variable in a multiple regression model can be linearly predicted from the others with a substantial degree of accuracy.