Momentum is conserved, m1→v i1 + m2→v i2 = m1→v f1 + m2→v f2 = (m1 + m2)→v f m 1 v → i 1 + m 2 v → i 2 = m 1 v → f 1 + m 2 v → f 2 = ( m 1 + m 2) v → f. V = (m 1 v 1 +m 2 v 2)/(m 1 +m 2) where, v= final velocity Similarly, there will only be one energy conservation equation.
AP Physics Momentum 2D Inelastic Collision Examples.wmv
P2 = 0.1 × v1 + 0.2 × v2.
Mass of object 1 × initial velocity 1 + mass of object 1 × initial velocity 1 = (mass of 1 + mass of 2) × final velocity of combined objects) in.
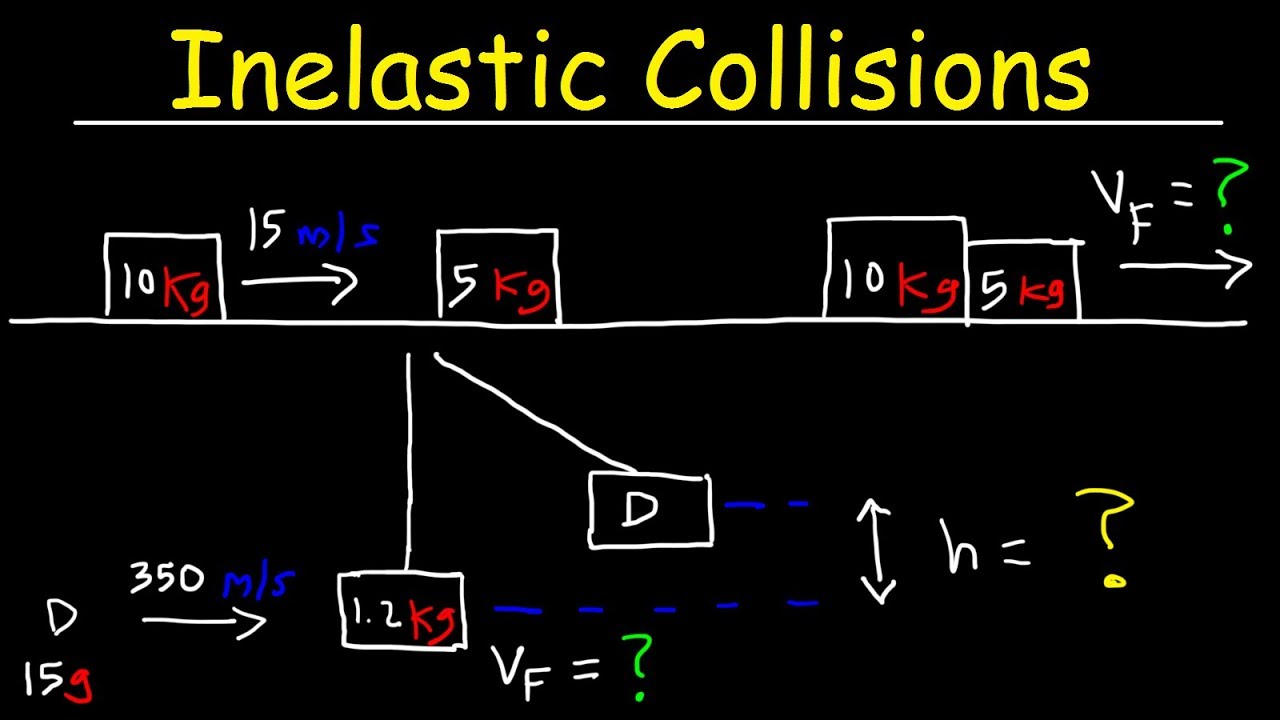
In a perfectly inelastic collision, the two collided bodies stick together and move with the same velocity v. In any closed system, momentum is conserved. The crash in which kinetic energy of the system is not conserved but the momentum is conserved, then that collision is termed as inelastic collision. M 1 u 1 = (m 1 + m 2)v.
So, the equation of conservation of momentum for inelastic collision is, m 1 u 1 + m 2 +u 2 = v(m 1 +m 2 ) the formula for final velocity after inelastic collision is,
An inelastic collisions occurs when two objects collide and do not bounce away from each other.momentum is conserved, because the total momentum of both objects before and after the collision is the same. Then fill in either the mass of b or the final velocity of a+b. Along with values, enter the known units of measure. The final velocity formula for a perfectly inelastic collision can be derived from the conservation of momentum.
V = m 1 u 1 +m 2 u 2 m 1 +m 2.
We are required to determine the final velocity of the resulting mass, →v f v → f. In this case, the forces between the colliding objects are conservative. All quantities are in si units. The momentum of the moving particle is m 22 45 4 1 4 3 1 5 mv pm v == = − ⎛⎞ −⎜⎟ ⎝⎠ m, and its energy is () m m 43 5 45 3 p m em v == =, for the composite particle, the conservation of energy implies that cm r 8 3 e =+=ee m, while the conservation of momentum implies that cm 4 3 pp==m.
Mass and velocity of a.
The perfectly elastic collision formula of momentum is followed as, m\[_{1}\]u\[_{1}\] + m\[_{2}\]u\[_{2}\] = m\[_{1}\]v\[_{1}\] + m\[_{2}\]v\[_{2}\] likewise, the conservation of the total kinetic energy is represented as, Mass of body 2 = m 2 the initial velocity of body 1 = u 1 the initial velocity of body 2 = u 2 The perfectly inelastic collision momentum formula is, the inelastic collision energy formula is, elastic collisions in an elastic collision, both momentum and energy are conserved. Momenta are conserved, hence p1 =.
Coefficient of restitution generally lies between 0 and 1.
The inelastic collision equation is: An example of real objects that have (approximately) elastic collisions are billiard balls. In an elastic collision, both momentum and kinetic energy are conserved. The momentum calculator uses the formula p=mv, or momentum (p) is equal to mass (m) times velocity (v).
It was established in the previous sections that.
Velocity of the stationary object after collision, in m/s. In this case, initial momentum is equal to 8 kg * 10 m/s + 4 kg * 0 m/s = 80 n·s. In all types of collision, momentum remains conserved. Where mass of body 1 = m 1.
The final velocity can be found for the two boys by rearranging the formula:
Thus, it is possible to equate momentum in the start and final states of a system and thus calculate an unknown. Coefficient of restitution is 0 for the perfectly inelastic collision. Mass of the stationary object, in kg. The final momentum of the first object is equal to 8 kg * 4 m/s = 32 n·s.
Mass of the moving object, in kg.
P2 the momentum of the two balls after collision is given by. Velocity of the moving object, in m/s. E f = ½ (m 1 + m 2)v 2, e i = ½ m 1 u 1 2. We know that the formula for momentum is given as formula:
The inelastic collision formula is articulated as.
Consequently, is momentum conserved in elastic and inelastic collisions? The total system momentum is. Pa = mass × velocity = 0.1 × 10 = 1 kg.m/s. Pb = mass × velocity = 0.2 × 5 = 1 kg.m/s.
The calc will provide the unknown mass or velociy of b.
That is, the total initial momentum of the system p~i is equal to the total final momentum p~f: The total momentum p~t of a system of n discrete parts can be expressed as the sum of each of the parts: In an inelastic collision kinetic energy is not conserved, but momentum is conserved. The momentum and energy of the particle at rest are rr p =0 em=.
According to the law of conservation of momentum, total momentum must be conserved.
Inelastic collision formula when two objects collide with each other under inelastic conditions, the final velocity of the object can be obtained as; P1 = pa + pb = 2 kg.m/s. The calculator can use any two of the values to calculate the third. The formula for inelastic collision:
Calculate the momentum of the system before the collision.
P~ t ˘m1 ~v1 ¯m2v~2 ¯¢¢¢¯mnv~n (2.2) when the sum of external forces acting on a system is zero, momentum is conserved. Since the collision is inelastic, we know that. Because momentum is a vector equation, there is only one momentum conservation equation. From, law of conservation of momentum we get to know that, p initial = p final