A , b et c pas de soucis. Matrice d'inertie 1/4 lycée lislet geoffroy sciences industrielles pour l’ingénieur matrice d'inertie d'un solide 1. Raemy démonstration du moment dʼinertie du cylindre creux dr f.
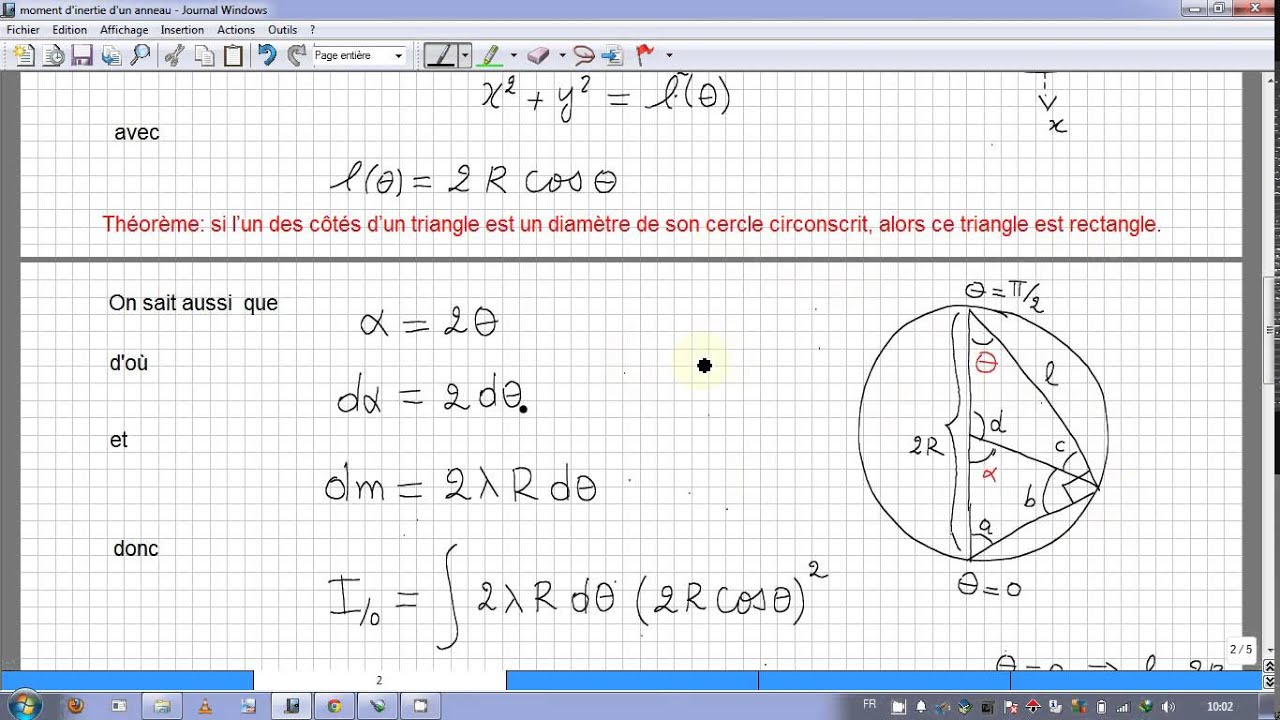
Calcul du moment d'inertie d'un triangle 01 YouTube
Le moment d'inertie d'un cylindre creux.
Moment d'inertie du cylindre creux.
Cône creux de rayon r et de hauteur h. Détermination de la base centrale d’inertie : Matrice d’inertie des solides élémentaires, 26 novembre 2006, 21:55, par pte nancy bonsoir, je suis tombé sur votre site qui est très bien fait et vraiment bien expliqué. Le moment quadratique est une grandeur qui caractérise la géométrie d'une section et se définit par rapport à un axe ou un point.
Le module de section est un élément indispensable pour le calcul de la résistance à la rupture de différents matériaux.
L’opérateur d’inertie est l’opérateur linéaire qui, a tout vecteur ,. L’axe (g,z) est axe de symétrie donc e=d=0. Élément d'inertie d'un solide par rapport aux éléments d’un repère 1.1. Pour calculer le moment d'inertie c = int ( r².dm ) mais pour le dm, je n'arrive pas a une expression satisfaisante :/ dm = ρ.ds avec ρ masse surfacique.
Les deux autres moments principaux d'inertie sont.
Pour les articles homonymes, voir moment. Il y a un nombre infini de combinaisons selon la forme du solide, le placement de son axe et son homgénéité. A, b, c étant les coordonnées de g dans le repère lié au solide s. Caractéristiques d’inertie des solides objectifs spécifiques :
En s’appuyant sur les notions vues en mécanique générale en 1er semestre
Le moment d'inertie mesure la résistance à l'accélération angulaire (la mise en rotation) d'un solide autour d'un axe. La méthode de calcul développée ci après permet de l'obtenir. 1) déterminez la matrice centrale d’inertie d’un cylindre de révolution plein et homogène de masse m , de rayon r et de hauteur h. Moments principaux d’inertie et repère principal d’inertie [haut de page] la.
Le passage d’une matrice d’inertie définie en g, centre d’inertie de s, à la matrice d’inertie en a s’écrit:
Il s'exprime donc en kg m 2. Sa hauteur est et le rayon de base est. Le volume du cône est le tiers de celui du cylindre : La variable radiale vaut , et les deux autres variables ont des variations inchangées pour décrire le pourtour du cylindre.
La masse du cône est.
Je calcule ensuite le moment d'inertie : Module de mécanique du solides indéformablechapitre 3: Ecrire la matrice d’inertie d’un solide par rapport à un repère. Ainsi le moment d'inertie principal vaut et présente, à masse égale, un effet plus inertiel qu'un cylindre plein.
Ecrire la matrice d’inertie d’un solide réel.
Quart de cercle de rayon r. Les symboles sont m qui représente la masse totale du cylindre et 0 r 0 le grand rayon, 0 r 0 le petit rayon. Soient un solide s de masse m et o un point de ce solide. Par contre je remarque qu’il n’y a pas la formule de la matrice d’inertie du cylindre creux, je pense que grâce à cette formule celle du cylindre, de la tige et.
Cylindre mince de rayon r et d'épaisseur faible.
L’énergie cinétique est par définition l’énergie k associéeau mouvement d’un corps. Question:déterminer la matrice d'inertie d'un cylindre creux en fonction de sa masse m, sa hauteur h et des rayons extérieur re et intérieur ri. R 0 2 2 + r 0 2 (2). Pour le cône creux, mon élément d'intégration est un cercle de rayon r et d'épaisseur dl.
Le moment d’inertie du cylindre creux dr f.
Déterminer le centre de gravité d’un solide. Raemy le moment d’inertie du cylindre creux est : Cylindre creux de rayons r1, r2 (rayons intérieur et extérieur) de hauteur h et de masse m. La notion d’opérateur d’inertie et la matrice qui lui est associée, permettent de définir complètement un solide du point de vue inertiel.
Déterminer la matrice d'inertie des solides homogènes suivants:
Définition le moment d'inertie par rapport à un plan ( π), une droite (. Moment d'inertie en serrant ses bras le long du corps, cette patineuse diminue son moment d'inertie, augmentant sa vitesse de rotation, puisque son moment. Il dépend de la forme, de la section de ces matériaux et est complémentaire au moment quadratique. La définition du moment d’inertie