Composite functions © jim west/the image works 1.8 sum, difference, product, and quotient of functions let and be two functions with overlapping domains. 6 , find the values of a and b. The squeeze theorem theorem 1 (squeeze theorem).
calculus Graph Limits of Composite Functions
Gf x 0 g f x x g x,
Composition of functions given functions f(u) and g(x), the composition f(g(x)) is the function of x formed by substituting u g(x) for u in the formula for f(u).
Limit of a composite function lim x→c f g(x) = lim x→c f(g(x)) = f(lim x→c g(x)) if f is continuous at lim x→c g(x). The limit of a composition is the composition of the limits, provided the outside function is continuous at the limit of the inside function. Notably, x 2 is not constant near π / 3 (or any other value for that matter). The limit is then evaluated as follows:
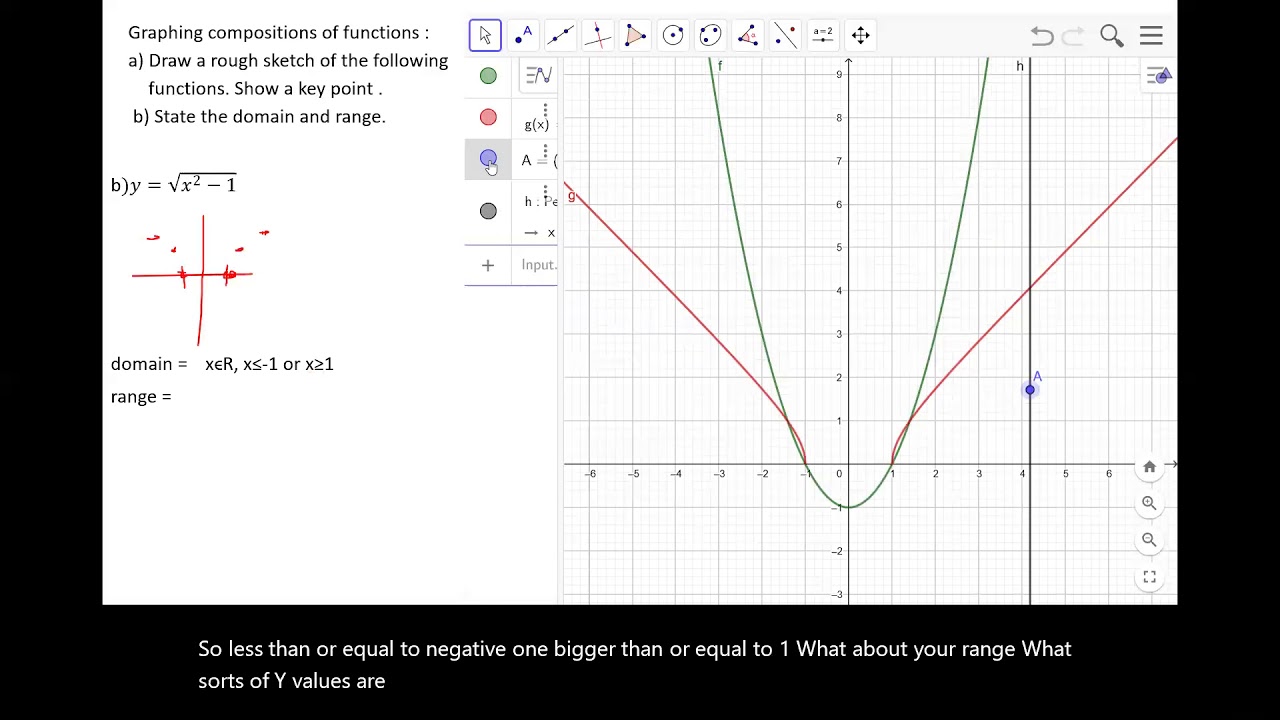
The graph of the function f (x) is given below.
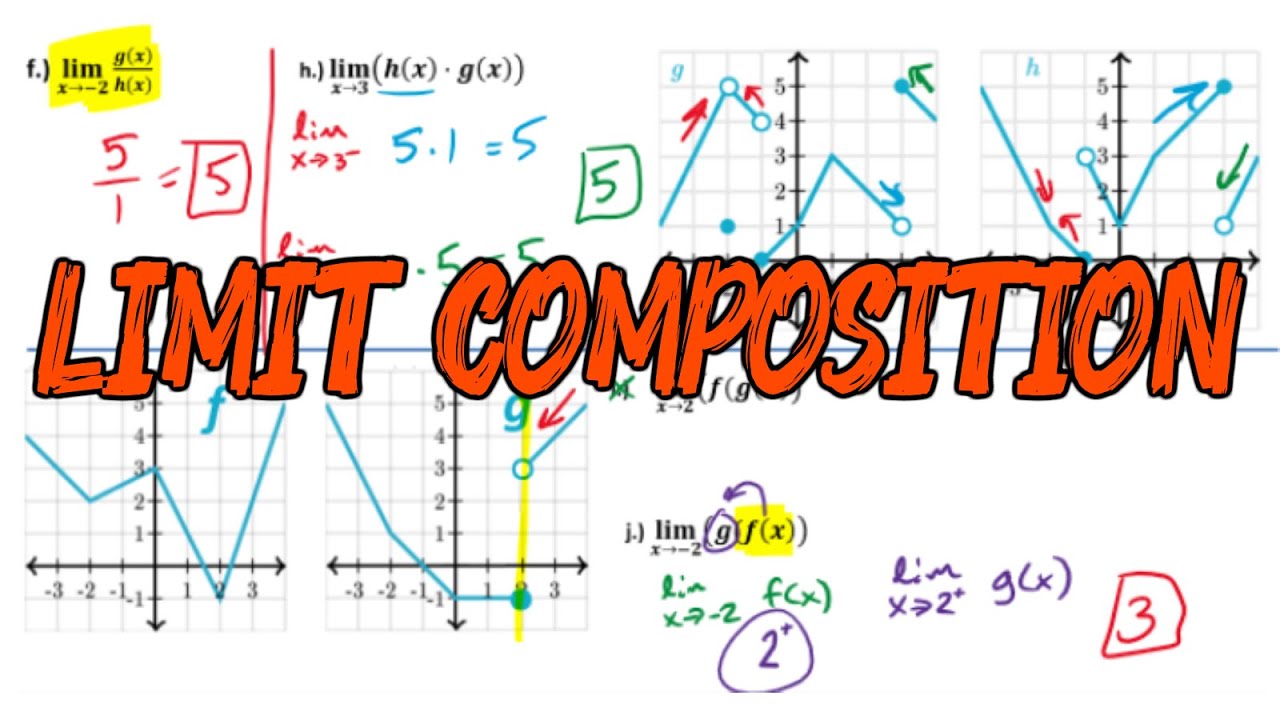
And these limits each sum to 4, so then it is said that the limit of the composition is 4. Use the graph of the function f(x) to answer each question. (a) if lim x → 1 f ( x )= 1 and lim x → 3 f ( x )=. Lim f [g(x)] = f [lim g(x)]
This chapter explains how to deal with them.
2 an introduction to limits what is a limit? 10.1 limits of the six trigonometric functions we start with the simple limit lim x!c sin(x). (a) f(0) = (b) f(2) = (c) f(3) = (d) lim x!0 f(x) = (e) lim x!0 f(x) = (f) lim x!3+ f(x) = (g) lim x!3 f(x) = (h) lim x!1 f(x) = 2. Consider the functions f ( x )= ax 2 − b x 2 − 4 and g ( x )= x 2 − cx + d x 2 − 4.
Derivatives derivative applications limits integrals integral applications integral approximation series ode multivariable calculus laplace transform taylor/maclaurin series fourier series.
We know that lim x → π / 3 x 2 = π / 3 by the limit law involving the limit of a. Let’s begin with the six trigonometric functions. Use 1, 1 or dnewhere appropriate. Limits of composite functions may be manipulated for easier evaluation.
The most important thing to know about evaluating limits of composite functions is that we can do so algebraically or graphically.
Limits of a composite function. Use the graph of the function f(x) to answer each question. A limit doesn't exist at the value that we are taking the limit of for each of the functions in the composition? Lim x→3 √ 5x+1 = √ 16 = 4.
F(x) g(t) t 2 1 x 3 6 chapter 1 functions, graphs, and limits
Here is a definition of functional composition. My limits & continuity course: Line equations functions arithmetic & comp. In particular, x 3 1 y.
Tions are formed and evaluated.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked. 3 suppose you are asked to sketch the graph of the function f given by for all values other than x = 1, you can use standard. Use 1, 1 or dnewhere appropriate. If you're seeing this message, it means we're having trouble loading external resources on our website.
Composite function limits worksheet 1 dk graph of f (x) f (x)= { − x, x − 2 2, − 2 x 1 − x+2, 1 x 3 4 , x=3 x−4, x > 3 graph of g (x) g (x)= { x+7, x − 2 − 2x+1, − 2 x 2 − 1, x 2 4 , 2 x 4 0, x > 4 find the value of the limit.
Find limits of a composition of two functions whose graphs are given. Given the following graphs of g and h, find the right side limit and left side limit of f(x) = (h o g)(x) in x = 1. Component functions and provisions for the limit of the composite. Lim x → π / 3 cos 3.
In this lesson, we learn how to evaluate a limit of a composition of two functions.
This video explains how to determine limits of composite function from the graphs of the two functions.site: Finding limits graphically and numerically objectives: Find lim x→ 0 f ( f. We have a new and improved read on this topic.
Here is the question, from drey:
Click create assignment to assign this modality to your lms. Then, for all common to both domains, the sum, difference, product, and quotient of and are defined as follows. Review (answers) to see the review answers, open this pdf file and look for section 2.8. The function can be partitioned into the composite components and.
Here x is a radian measure because we are taking sin of it.
Composition of functions y t 2; (a) f(0) = (b) f(2) = (c) f(3) = Limits of trigonometric functions some limits involve trigonometric functions. If lim g ( x) = a and function f is continuous at a, it follows that: