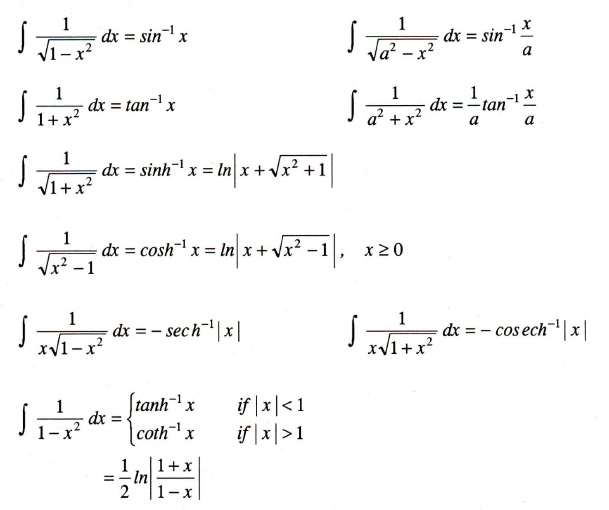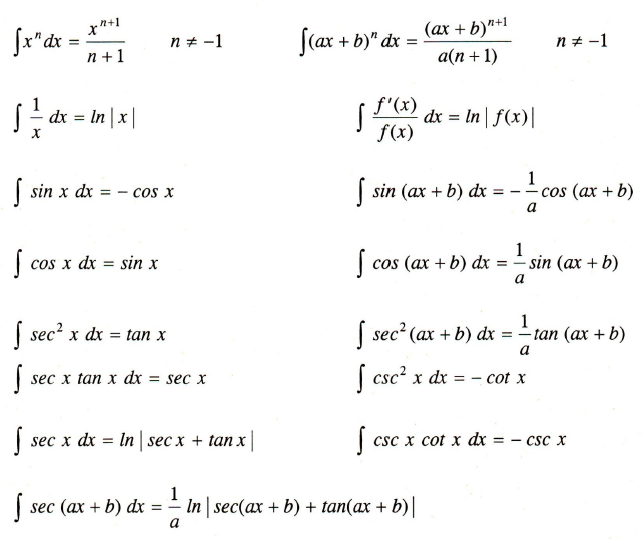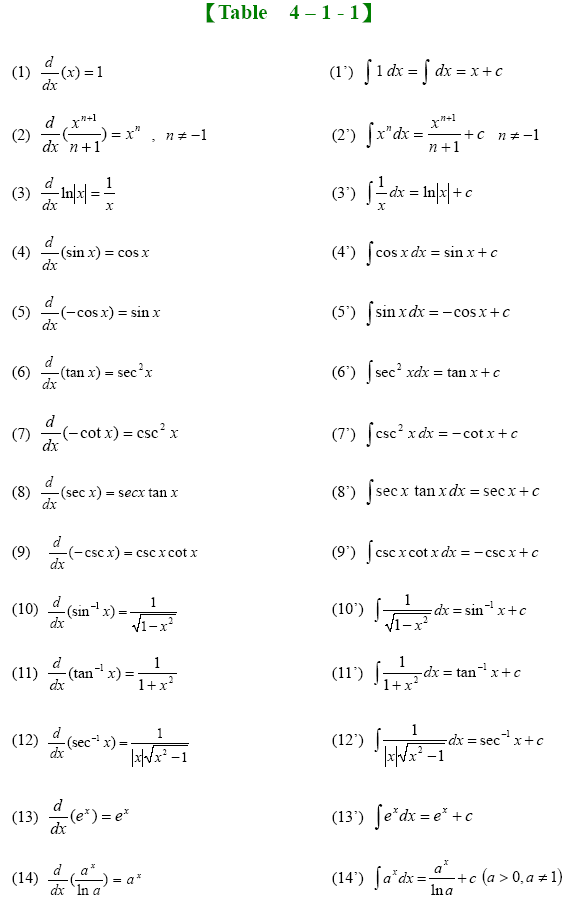Students, teachers, parents, and everyone can find solutions to their math problems instantly. A table of integrals f(x) r f(x)dx k, any constant kx+c. X dx= 2 ax+ b+ b xyax+ b' 26.
Integral table
Type in any integral to get the solution, steps and graph
Free math lessons and math homework help from basic math to algebra, geometry and beyond.
Integration can be used to find areas, volumes, central points and many useful things. 3 2;cos2 ax (75) z cosaxdx= 1 a sinax (76) z cos2 axdx= x 2 + sin2ax. (of course, use a computer to do integrals whenever you can!) points to note: This section documents the layout of the integration database tables.
Sometimes restrictions need to be placed on the values of some of the variables.
N 6= 1 (2) z 1 x dx = lnjxj (3) z u dv = uv z vdu (4) z e xdx = e (5) z ax dx = 1 lna ax (6) z lnxdx = xlnx x (7) z sinxdx = cosx (8) z cosxdx = sinx (9) z tanxdx = lnjsecxj (10) z secxdx = lnjsecx+tanxj (11) z sec2 xdx = tanx (12) z secxtanxdx = secx (13) z a a2 +x2 dx = tan 1 x a (14) z a a2. Microsoft dataverse and business central store dates in different formats. 1.3 the fundamental theorem of calculus; Example evaluate i = z dx √ 2x3 +3x2, for x > 0.
Table of integrals basic forms z xndx= 1 n+ 1 xn+1 (1) z 1 x dx= lnx (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2 dx= 1 x+ a (5) z (x+ a)ndx= (x+ a)n+1 n+ 1 + c;n6= 1 (6) z x(x+ a)ndx= (x+ a)n+1((n+ 1)x a) (n+ 1)(n+ 2) (7) z 1 1 + x2 dx= tan 1 x (8) z 1 a2 + x2 dx= 1 a tan 1 x a (9) z x a 2.
Table of useful integrals, etc. Integrals with trigonometric functions (71) z sinaxdx= 1 a cosax (72) z sin2 axdx= x 2 sin2ax 4a (73) z sin3 axdx= 3cosax 4a + cos3ax 12a (74) z sinn axdx= 1 a cosax 2f 1 1 2; A lot of the integrals in this section can easily be done using a table of integrals. If a term in your choice for yp happens to be a solution of the homogeneous ode corresponding to (4), multiply this term by x (or by x 2 if this solution corresponds to a double root of the
This page lists some of the most common antiderivatives
For example, the account integration table connects to the accounts table in dataverse. We start rewriting our integral as E−ax2dx= 1 2 π a # $% & ’(1 2 0 ∞ ∫ ax xe−2dx= 1 2a 0 ∞ ∫ x2e−ax2dx= 1 4a π a # $% & ’(1 2 0 ∞ ∫ x3e−ax2dx= 1 2a2 0 ∞ ∫ x2ne−ax2dx= 1⋅3⋅5⋅⋅⋅(2n−1) 2n+1an π a $ %& ’ 1 2 0 ∞ ∫ x2n+1e−ax2dx= n! Integration tables include fields that correspond to columns in the dataverse table.
These tables are used by the identity governance and intelligence integration interface to exchange information between access governance core and external repositories that reside in target systems.
It's very important to understand the substitutions `u` and `du` (which is the case for most integrations) make sure you use the correct formula!! Integration is the basic operation in integral calculus.while differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. Table of basic integrals1 (1) z xn dx = 1 n+1 xn+1; This calculus video tutorial explains how to do integration by tables.
An integration table is a table in the business central database that represents an table, such as an account, in dataverse.
Imports data about organization units. This leaflet provides such a table. 1.6 integrals involving exponential and logarithmic functions; Table of integrals engineers usually refer to a table of integrals when performing calculations involving integration.
These restrictions are shown in the third column.
There must be a integration table mapping for. Sometimes to use integration tables one needs to rewrite the integral in the form that appears in the table. Table 2.1, choose yp in the same line and determine its undetermined coefficients by substituting yp and its derivatives into (4). You need to be able to identify the appropriate integration formulas to find the inde.
Sometimes we can work out an integral, because we know a matching derivative.
Integrals with trigonometric functions z sinaxdx = 1 a cosax (63) z sin2 axdx = x 2 sin2ax 4a (64) z sinn axdx = 1 a cosax 2f 1 1 2, 1 n 2, 3 2,cos2 ax (65) z sin3 axdx = 3cosax 4a + cos3ax 12a (66) z cosaxdx = 1.7 integrals resulting in inverse trigonometric functions Table of integrals∗ basic forms z xndx = 1 n+ 1 xn+1 (1) z 1 x dx= lnjxj (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2 dx= ln(1 x+ a (5) z (x+ a)ndx= (x+ a)n+1 n+ 1;n6= 1 (6) z x(x+ a)ndx= (x+ a)n+1((n+ 1)x a) (n+ 1)(n+ 2) (7) z 1 1 + x2 dx= tan 1 x (8) z 1 a2 + x2 dx= 1 a tan 1 x a (9) z. The fundamental theorem of calculus establishes the relationship between indefinite and definite.
The first rule to know is that integrals and derivatives are opposites!.