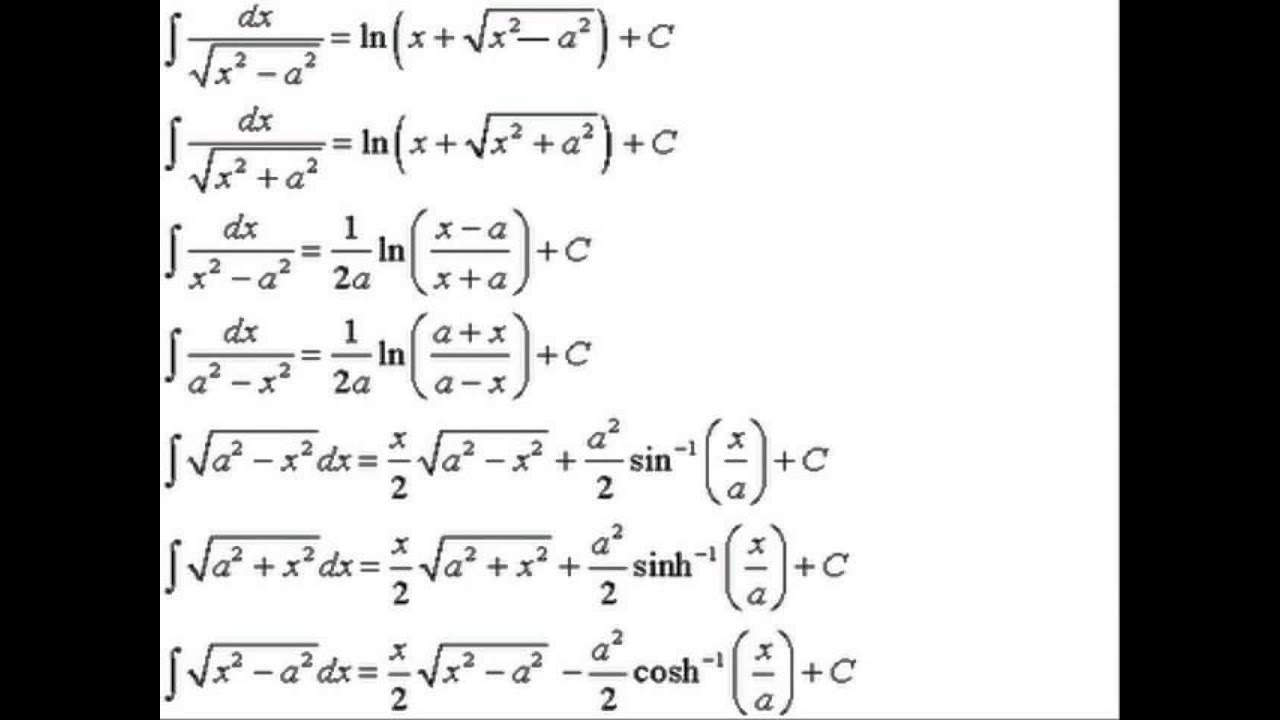\displaystyle\int {e}^ { { {2} {x}}}\ \sin { {3}} {x}\ {\left. Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − integrals of rational and irrational functions 1 1 n x dx cn x n + = + ∫ + 1 dx x cln x ∫ = + ∫cdx cx c= + 2 2 x ∫xdx c= + 3 2 3 x ∫x dx c= + ∫1/x.dx = log|x| + c;
Pin by Tony Wong on karim Studying math, Mathematics
N6= 1 (2) z 1 x dx= lnjxj (3) z udv= uv z vdu (4) z 1 ax+ b dx= 1 a lnjax+ bj integrals of rational functions (5) z 1 (x+ a)2 dx= 1 x+ a (6) z (x+ a)ndx= (x+ a)n+1 n+ 1;n6= 1 (7) z x(x+ a)ndx= (x+ a)n+1((n+ 1)x a) (n+ 1)(n+ 2) (8) z 1 1 + x2 dx= tan 1 x (9) z 1 a2 + x2 dx= 1 a tan 1 x a 1
Tabular integration is a short method for integration to solve the integral problem quickly, instead of using the lengthy and tedious process of integration by parts traditional method.
∫ ( d d x ( f ( x)) ∫ ( g ( x)) d x) d x. This formula relates a complicated integral to a simpler integral. If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions. Integral of the form ∫ (px+q) √( ax 2 + bx + c ) dx we solve this using a specific method.
∫ e x.dx = e x + c;
{d} {x}\right.} ∫ e2x sin3x dx. The integral formulas for some special functions listed below: 2 22 a sin b a bx x− ⇒= θ cos 1 sin22θθ= − 22 2 a sec b bx a x− ⇒= θ tan sec 122θθ= − 2 22 a tan b a bx x+ ⇒= θ sec 1 tan2 2θθ= + ex. (i) when you find integral ∫g (x) dx then it will not contain an arbitrary constant.
Basic forms z xndx = 1 n +1 xn+1(1) z 1 x dx =ln|x| (2) z udv = uv z vdu (3) z 1 ax + b dx = 1 a ln|ax + b| (4) integrals of rational functions z 1 (x + a)2.
∫ u d u a + b u = 1 b 2 ( a + b u − a ln | a + b u | ) + c ∫ u d u a + b u = 1 b 2 ( a + b u − a ln | a + b u | ) + c ∫ a x.dx = a x /loga+ c Some generalised results obtained using the fundamental theorems of integrals are remembered as integration formulas in indefinite integration. Table of integrals basic forms (1)!xndx= 1 n+1 xn+1 (2) 1 x!dx=lnx (3)!udv=uv!vdu (4) u(x)v!(x)dx=u(x)v(x)#v(x)u!(x)dx rational functions (5) 1 ax+b!dx= 1 a ln(ax+b) (6) 1 (x+a)2!dx= 1 x+a (7)!(x+a)ndx=(x+a)n a 1+n + x 1+n #$ % &', n!1 (8)!x(x+a)ndx= (x+a)1+n(nx+xa) (n+2)(n+1) (9) dx!1+x2 =tan1x (10) dx!a2+x2 = 1 a tan1(x/a) (11) xdx!a2+x2.
Below are the integration basic formulas for your ready reference:
Find the following integral, using table of integrals: A s2 1 area of a triangle: The advantage of the tabular integration method is that it can save huge time in solving the problem. For this example, we use:
(ii) ∫g (x) dx should be taken as the same in both terms.
We can rewrite the integral as i = z dx p x4(4x +9) = z dx x2. Z xn dx = xn+1 n+1 if n 6= −1 d dx (xn) = nxn−1 z sinxdx = −cosx+c d dx (cosx) = −sinx z cosxdx = sinx+c d dx (sinx) = cosx z sec2 xdx = tanx+c d dx (tanx) = sec2 x z e xdx = e x+c d dx (e ) = e z 1 x dx = lnx+c d dx (lnx) = 1 x z kdx = kx+c d dx (kx) = k structural type formulas 1.1 dx = x + c 1.2 k dx = k x + c , where k is a constant. It gives the solution fairly accurate than the integration by parts method.
If we substitute f (x) = t, then f’ (x) dx = dt.
This gives the following formulas (where a ≠ 0 ), which are valid over any interval where f is continuous (over larger intervals, the constant c must be replaced by a piecewise constant function): For the following, the letters a, b, n, and c represent constants. Basic forms z xndx = 1 n+ 1 xn+1(1) z 1 x dx= lnjxj (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2. Let’s have a look at the additional integration formulas, i.e.
Integration u'vdx(byparts) uv —cos x + c sin x + c in eos + c in + c in + + c in — cot xl + c — amtan — arcsin — arcs inh — arccosh — + c — åsin2r+c tan x — x + c —cot x— x + c du sin x tan sec dr esc dr sin2 x dr dr tan2 x dr cot2 x dr du dy (chain rule) ae —sin cosh x.
Also, get some more complete. ∫ e 2 x sin 3 x d x. First we write px + q = a (d(√(ax 2 + bx + c))/dx) + b Table of basic integrals basic forms (1) z xndx= 1 n+ 1 xn+1;
Integration formulas z dx = x+c (1) z xn dx = xn+1 n+1 +c (2) z dx x = ln|x|+c (3) z ex dx = ex +c (4) z ax dx = 1 lna ax +c (5) z lnxdx = xlnx−x+c (6) z sinxdx = −cosx+c (7) z cosxdx = sinx+c (8) z tanxdx = −ln|cosx|+c (9) z cotxdx = ln|sinx|+c (10) z secxdx = ln|secx+tanx|+c (11) z cscxdx = −ln |x+cot +c (12) z sec2 xdx = tanx+c (13) z csc2 xdx = −cotx+c (14) z
16 x2 49 x2 dx ∫ − 22 x. ∫ x n.dx = x (n + 1) /(n + 1)+ c; We recognize this is the required formula: √ ax +b = − √ ax +b bx − a 2b z dx x √ ax +b.
∫ | ( a x + b ) n | d x = sgn ( a x + b ) ( a x + b ) n + 1 a ( n + 1 ) + c {\displaystyle \int.
Sin x, cos x, tan x, cot x, sec x and csc x. The following table lists integration formulas side by side with the corresponding differentiation formulas. ∫ 1.dx = x + c; Entry (15) in the integration tables at the end of the textbook is z dx x2.
In what follows, c is a constant of integration and can take any constant value.
2 1 sin ( ) 1 cos(2 )x 2 sin tan cos x x x 1 sec cos x x cos( ) cos( ) x x 22sin ( ) cos ( ) 1xx 2 1 cos ( ) 1 cos(2 )x 2 cos cot sin x x x 1 csc sin x x sin( ) sin( ) x x 22tan ( ) 1 sec ( )x x geometry fomulas: Most of the following integral entries are written for indefinite integrals, but.