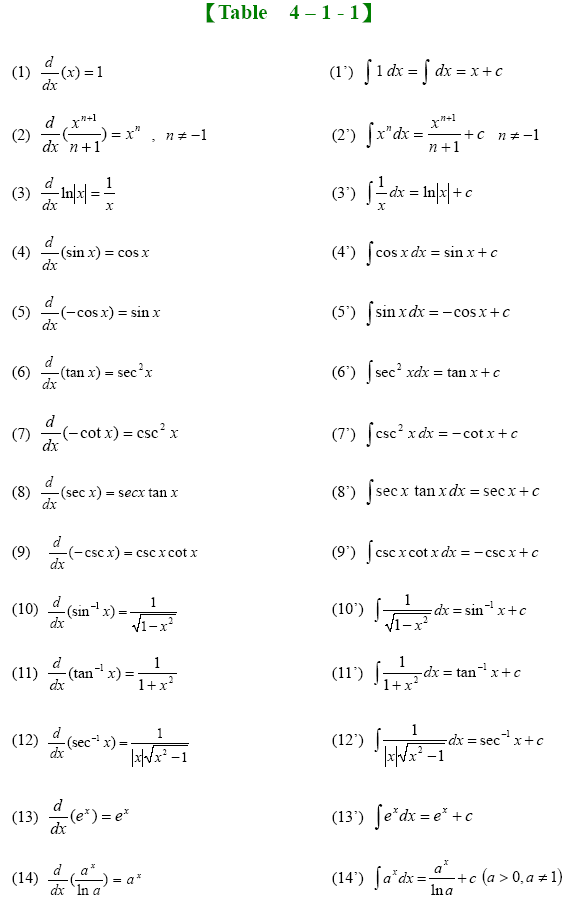Generally, we can write the function as follow: Dx= ln( 1 x+ a (5) z (x+ a)ndx= (x+ a)n+1. Ln x a dx cx a a ³ 5.
integration calculus Studying math, Mathematics
X (21) x (22) !
The most common application of integration is to find the area under the curve on a graph of a function.
Integration using tables while computer algebra systems such as mathematica have reduced the need for integration tables, sometimes the tables give a nicer or more useful form of the answer than the one that the cas will yield. Table of basic integrals basic forms (1) z xndx= 1 n+ 1 xn+1; ∫ cos u d u = sin u + c ∫ cos u d u = sin u + c. (d/dx) (sinx + c)= cos x +0.
If r (x) in (4) is one of the functions in the first column in table 2.1, choose yp in the same line and determine its undetermined coefficients by substituting yp and its derivatives into (4).
³csc cot2 xdx x c 11. Udv = uv ! View integral table.pdf from ee 3340 at idaho state university. (x)dx n x !
³sin cosxdx x c 8.
If a term in your choice for yp happens to be a While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. Vdu (4) u (x)v! ³cos sinxdx x c 9.
Inthefollowingtable,theconstantofintegration,c,isomittedbut shouldbeaddedtotheresultofeveryintegration.theletterx represents anyvariable;u representsanyfunctionofx;
Where “c” is the arbitrary constant or constant of integration. The curve c with equation y = f (x) passes through the point (5, 65). ³e dx e cxx 4. ∫ cos x dx = sin x + c.
To work out the integral of more complicated functions than just the known ones, we have some integration rules.
∫ csc 2 u d u = −cot u + c ∫. This page lists some of the most common antiderivatives. ∫ e u d u = e u + c ∫ e u d u = e u + c. 1 1 n x dx cn x n ³ reciprocal, exponential, log 2.
So, equation (1) can be written as.
³sec tan2 xdx x c 10. ³sec tan secx xdx x c 12. Dx = 1 x + a (5) z (x + a)ndx = (x + a)n+1. 1 dx x cln x ³ 20.
Integral table basic properties of integration f ( x ) dx = f ( x ) + c , if f ( x ) = f ( x ) f ( x ) dx = f ( x ) af ( x ) dx = a
Also, any real number “c” is considered as a constant function and the derivative of the constant function is zero. Table of basic integrals1 (1) z xn dx = 1 n+1 xn+1; This video provides an example of how apply an integration formula that involving a^2+u^2. (73) ∫ sin nax dx = − 1 a cos ax 2f1[1 2, 1 − n 2, 3 2, cos 2ax] (74)
(72) ∫ sin 3ax dx = − 3 cos ax 4a + cos 3ax 12a.
Table of integrals basic forms integrals with roots 1 (1) ! (x)dx = u (x)v (x) # v (x)u ! ∫ f dx + ∫ g dx: ³ln lnx dx x x x c 6.
(d/dx) (sinx + c)= cos x.
Table of integrals basic forms (1)!xndx= 1 n+1 xn+1 (2) 1 x!dx=lnx (3)!udv=uv!vdu (4) u(x)v!(x)dx=u(x)v(x)#v(x)u!(x)dx rational functions (5) 1 ax+b!dx= 1 a ln(ax+b) (6) 1 (x+a)2!dx= 1 x+a (7)!(x+a)ndx=(x+a)n a 1+n + x 1+n #$ % &', n!1 (8)!x(x+a)ndx= (x+a)1+n(nx+xa) (n+2)(n+1) (9) dx!1+x2 =tan1x (10) dx!a2+x2 = 1 a tan1(x/a) (11) xdx!a2+x2. ∫ x n dx = ( (x n+1 )/ (n+1))+c ; ∫ a u d u = a u ln a + c ∫ a u d u = a u ln a + c. ∫ 1 dx = x + c.
X n+1 n+1 + c:
N 6= 1 (2) z 1 x dx = lnjxj (3) z u dv = uv z vdu (4) z e xdx = e (5) z ax dx = 1 lna ax (6) z lnxdx = xlnx x (7) z sinxdx = cosx (8) z cosxdx = sinx (9) z tanxdx = lnjsecxj (10) z secxdx = lnjsecx+tanxj (11) z sec2 xdx = tanx (12) z secxtanxdx = secx (13) z a a2 +x2 dx = tan 1 x a (14) z a a2 x2 dx = 1 2 ln x+a x a (15) z 1 p a2 2x dx = sin 1 x a. ∫ d u u = ln | u | + c ∫ d u u = ln | u | + c. Basic integral table power functions 1. Integration is used to find many useful parameters or quantities like area, volumes, central points, etc., on a large scale.
Basic trig and exponential examples that use rules from the table of integrals, as well as trig identities.
This video provides an example of how apply an integration formula that involving a^2+u^2. 1 dx = 2 x ± a x±a (20) 1 dx = 2 a ! Type in any integral to get the solution, steps and graph this website uses cookies to ensure you get the best experience. Ln log a ln x x x x dx c a ³ trig functions 7.
∫ sec x (tan x) dx = sec x + c.
N6= 1 (2) z 1 x dx= lnjxj (3) z udv= uv z vdu (4) z 1 ax+ b dx= 1 a lnjax+ bj integrals of rational functions (5) z 1 (x+ a)2 dx= 1 x+ a (6) z (x+ a)ndx= (x+ a)n+1 n+ 1;n6= 1 (7) z x(x+ a)ndx= (x+ a)n+1((n+ 1)x a) (n+ 1)(n+ 2) (8) z 1 1 + x2 dx= tan 1 x (9) z 1 a2 + x2 dx= 1 a tan 1 x a 1 The list of basic integral formulas are. ∫ u n d u = u n + 1 n + 1 + c, n ≠ − 1 ∫ u n d u = u n + 1 n + 1 + c, n ≠ − 1. Power rule (n≠−1) ∫ x n dx:
Basic forms z xndx = 1 n +1 xn+1(1) z 1 x dx =ln|x| (2) z udv = uv z vdu (3) z 1 ax + b dx = 1 a ln|ax + b| (4) integrals of rational functions z 1 (x + a)2.
∫ sin ax dx = − 1 a cos ax. X dx = n + 1 x (2) ! ∫ sec 2 u d u = tan u + c ∫ sec 2 u d u = tan u + c. Basic forms z xndx = 1 n+ 1 xn+1(1) z 1 x dx= lnjxj (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2.
³csc cot cscx xdx x c 13.
∫ (f + g) dx: (71) ∫ sin 2ax dx = x 2 − sin 2ax 4a. Integration is the basic operation in integral calculus. ∫ sin u d u = −cos u + c ∫ sin u d u = −cos u + c.
∫ sec 2 x dx = tan x + c.