Fundamental rules ( ) 𝑥 =0 ∫ 𝑥=𝑥+𝐶 The first one is that you can apply limits after the end of your integrating result as you did in indefinite integration but make sure your variable is the same. Basic integration, rules and example of integration, composite integrals, examples of standard integrals
core pure 3 notes integration by parts examples
If d/dx(f(x) = f(x), then ∫ f(x) dx = f(x) +c.
If you find that your integral is difficult to solve using normal methods of integration, for example when calculating the arc length (ℓ) of an hyperbola using the universal hyperbolic formula;
This rule is also called the antiderivative quotient or division rule. Then the integration of 5 x 4 with respect to x is x 5. You can see from the example above, the only difference between the sum and difference rule is the sign symbol. Z ex dx= ex + c if we have base eand a linear function in the exponent, then z eax+b dx= 1 a eax+b + c trigonometric functions z
The formula for the integral division rule is deduced from the integration by parts u/v formula.
Integration by part is a little complex rule. Apr 11 6:05 pm (4 of 15) title: The integral quotient rule is the way of integrating two functions given in form of numerator and denominator. If a function is integrable and if its integral over the domain is finite, with the limits specified, then it is the definite integration.
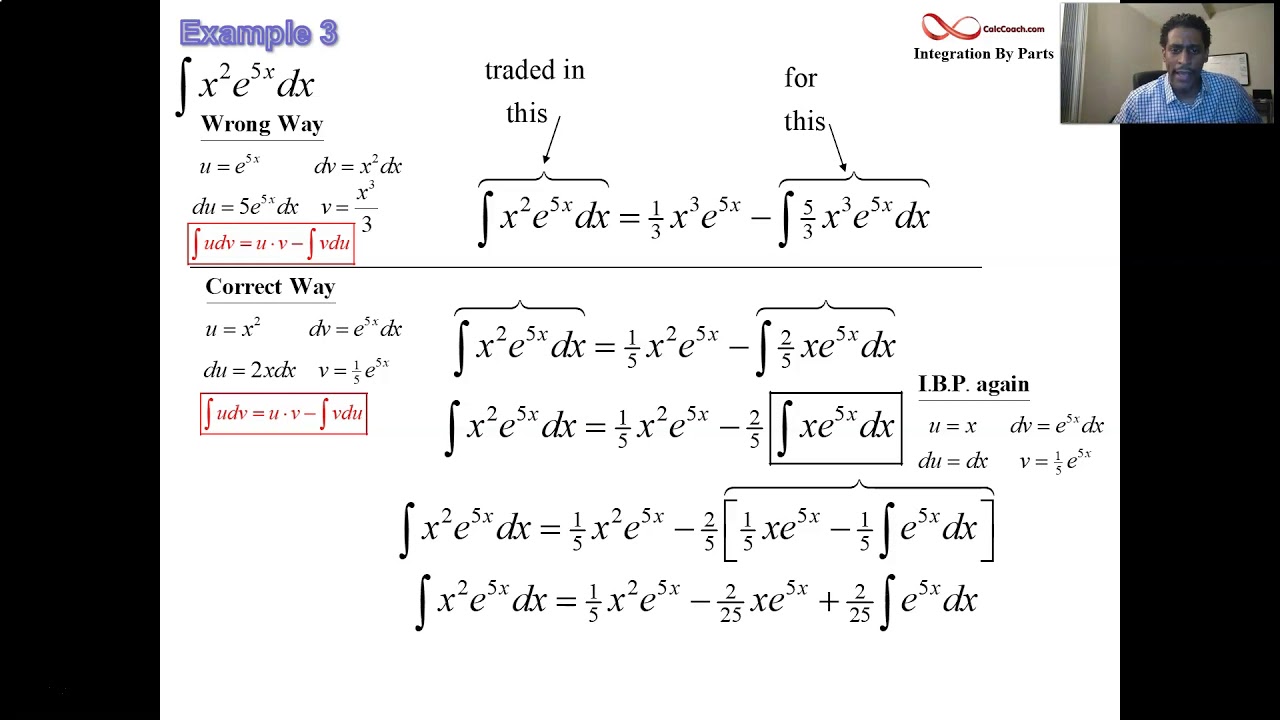
The following diagrams show some examples of integration rules:
Integration is the process of finding the antiderivative of a function. ∫ (fx + gx).dx = ∫ fx.dx + ∫ gx.dx. Let’s take an example of \int _ { a } ^ { b } f ( y ) dx ⇒ first, solve the integration of this function ∫[f(u) du/dx] dx = ∫f(u) du example:
For the following, let u and v be functions of x, let n be an integer, and let a, c, and c be constants.
∫ (y 2 + 2).dy = ∫ y 2.dy + ∫ 2.dy = y 3 /3 + 0 (applying power and constant rule) = y 3 /3 + c. These are some of the most frequently encountered rules for differentiation and integration. Here is the power rule once more: ∫ 5x⁴ dx = 5 ∫ x⁴ dx.….
Therefore for the above examples, we usually write.
Generally, we can write the function as follow: Apr 11 6:04 pm (3 of 15) title: Rules for solving integration by parts for definite integral limits. Apr 11 6:05 pm (5 of 15) title:
Power rule for integration the power rule for integration provides us with a formula that allows us to integrate any function that can be written as a power of \(x\).
Where “c” is the arbitrary constant or constant of integration. Power rule, exponential rule, constant multiple, absolute value, sums and difference. (d/dx) [f (x)+c] = f (x), where x belongs to the interval i. To represent the antiderivative of “f”, the integral symbol “∫” symbol is introduced.
It is the inverse of the product rule of differentiation.
Some simple examples here are some simple examples where you can apply this technique. Integration is the reverse process of differentiation. Apr 11 6:06 pm (6 of 15) title: Integration rules and techniques antiderivatives of basic functions power rule (complete) z xn dx= 8 >> < >>:
What is ∫ 5x⁴ dx ?
Suppose the derivative of x 5 is 5x 4. These integrals are also called improper integrals or indefinite integrals Xn+1 n+ 1 + c; 10 rows for example, to derive the integration rule for∫ cos x dx, just think the derivative of what.
By the end of this section we'll know how to evaluate integrals like:
Ax n d x = a. If n6= 1 lnjxj+ c; Apr 11 5:59 pm (1 of 15) title: Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − integrals of rational and irrational functions 1 1 n x dx cn x n + = + ∫ + 1 dx x cln x ∫ = + ∫cdx cx c= + 2 2 x ∫xdx c= + 3 2 3 x ∫x dx c= +
We use this in symbol as follows:
∫ 7 dx = 7 ∫ dx. If n= 1 exponential functions with base a: Consider the integral ∫(2 x + 1) 3 dx toview the thing we are integrating asa composition, introduce the functions f · (x) = x3, g(x) = 2 x + 1 this does the jobin the sense that f · (g(x))= (2 x + 1) 3 butrecall thatthe patternwe have totry andforce the problem into is ∫f Z ax dx= ax ln(a) + c with base e, this becomes:
Scroll down the page for more examples and solutions on how to integrate using some rules of integrals.
∫ 7 dx = 7 ∫ dx.……multiplication by a constant rule = 7x + c. In both of these rules, integration is applied separately on the functions and then they are subtracted or added accordingly. Apr 11 6:03 pm (2 of 15) title: \[\int 4x^3 dx\] \[\int \frac{3}{x^2}dx\] \[\int \begin{pmatrix} 2x + 3 \sqrt{x} \end{pmatrix} dx \] we start by learning the power rule for integration.
The power rule for integration, as we have seen, is the inverse of the power rule used in differentiation.
It gives us the indefinite integral of a variable raised to a power.