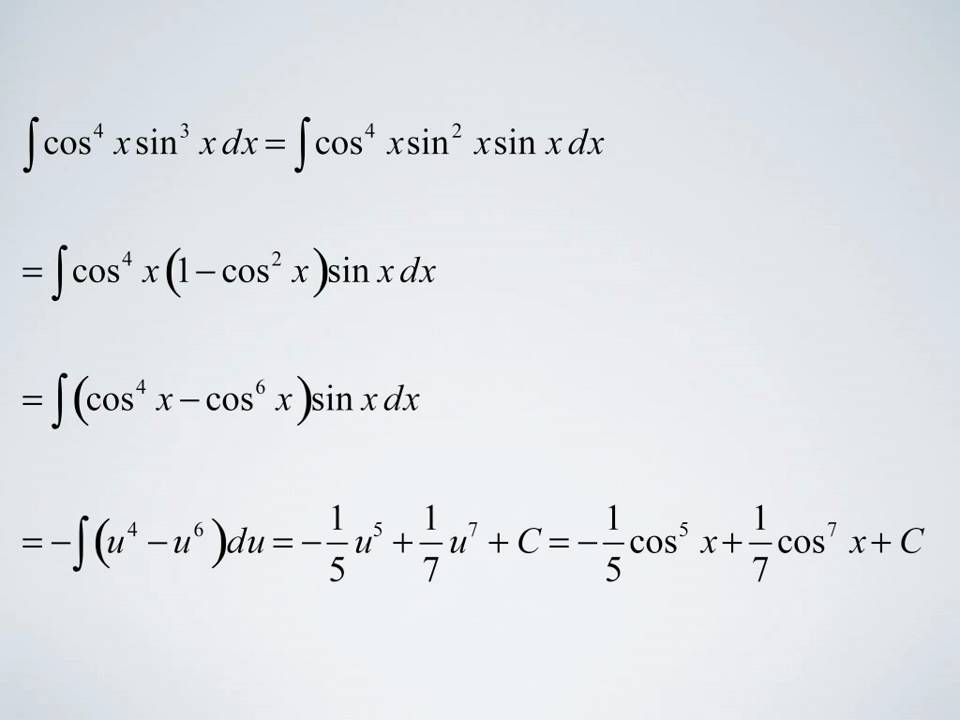In a simple straight language integration can be defined as the measure, which basically assigns numbers to the several functions.the numbers are basically assigned which may describe the displacement,volume or area etc of such concerned function. Fundamental rules ( ) 𝑥 =0 ∫ 𝑥=𝑥+𝐶 Is an odd integer :
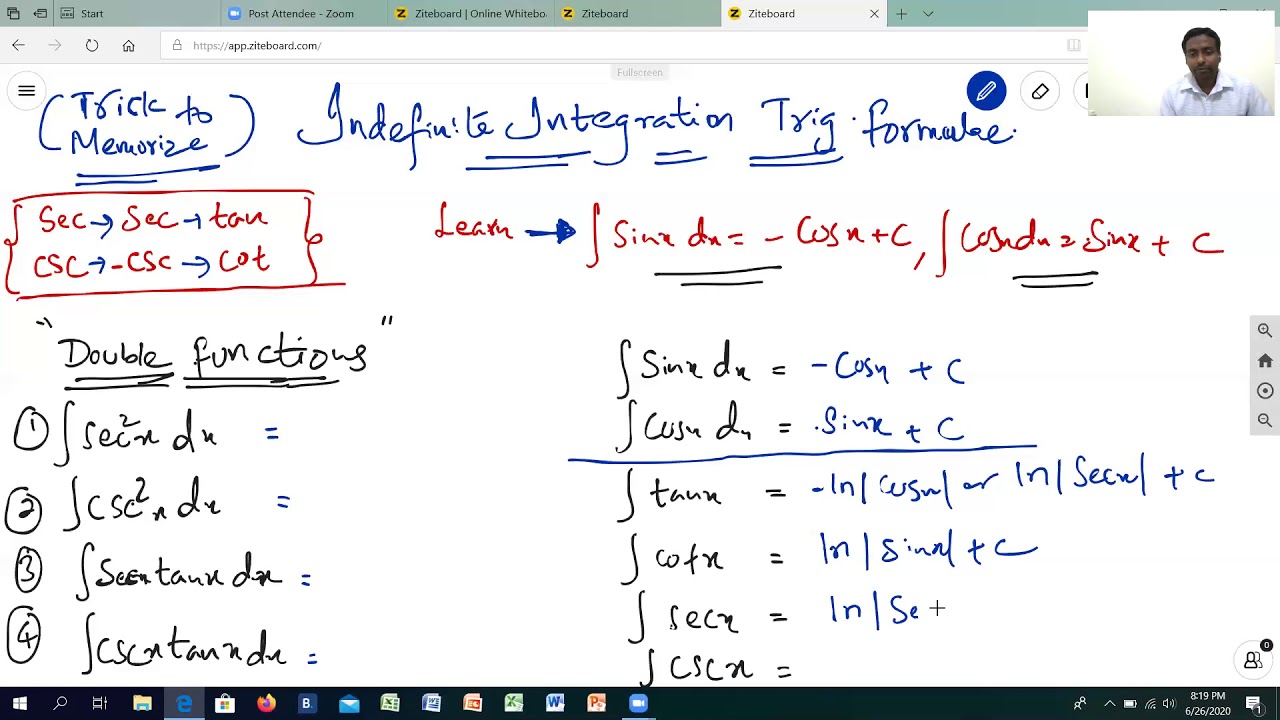
List of Integrals of Trig and Inverse Trig Functions
∫ (f + g) dx:
Sin5(x) = sin4(x)sin(x) = h sin2(x) i 2 sin(x) = h 1 cos2(x) i 2 sin(x) and then integrate, using the substitution u = cos(x) )du = sin(x)dx:
We change sin’s to cos’s or cos’s to sin’s via pythagorean’s theorem: In integration we basically take the infinitesimal data as the combination. Now recall the trig identity, cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x. Recall the definitions of the trigonometric functions.
Change all sin’s to cos’s except for one, or vice versa.
Here are some hints to help you remember the trig differentiation and integration rules: Sin2(x) + cos2(x) = 1 example 1. When the trig functions start with “ c ”, the differentiation or integration is negative (cos and csc). D x + ∫ g ( x).
Lastly, we will see how to.
For the functions other than sin and cos , there’s always either one tan and two secants , or one cot and two cosecants on either side of the formula. Integrals involving sin(x) and cos(x): If the function we are integrating is just a product of sin(x) and cos(x) our general strategy is the same: Generally, if the function is any trigonometric function, and is its derivative, in all formulas the constant a is assumed to be nonzero, and c.
Integration with inverse trigonometric functions a.
The following are some standard trigonometric integration formulas with proofs. What is so important to remember, as interactive mathematics, accurately states, we are going to use our knowledge of the derivatives and reverse the differentiation processes. X n+1 n+1 + c: According to the properties of integration, the integral of sum of two functions is equal to the sum of integrals of the given functions, i.e., ∫ [ f ( x) + g ( x)] d x = ∫ f ( x).
These are some of the most frequently encountered rules for differentiation and integration.
Therefore equation 1 can be rewritten as: Integration rules and techniques antiderivatives of basic functions power rule (complete) z xn dx= 8 >> < >>: First split off one power of sine, writing: Integrals involving sec(x) and tan(x):
If the power of the sine is odd and positive:
The integrals in example 1 are fairly straightforward applications of integration formulas. Sin 1 y q==y 1 csc y q= ∫ ( 1 + c o s 2 x) d x = ∫ 1 d x + ∫ c o s 2 x d x. Save a du x dx sin( ) ii.
A.) b.) e.) it is assumed that you are familiar with the following rules of differentiation.
Z ex dx= ex + c if we have base eand a linear function in the exponent, then z eax+b dx= 1 a eax+b + c trigonometric functions z sin(x)dx= cos(x) + c z On occasions a trigonometric substitution will enable an integral to be evaluated. Integration using trig identities or a trig substitution some integrals involving trigonometric functions can be evaluated by using the trigonometric identities. The formulas are incredibly straightforward and easy to memorize, as they all follow a very similar pattern.
1 3 arcsec 2x 3 c u 2x, a 3 dx
Trigonometric integrals r sin(x)dx = cos(x)+c r csc(x)dx =ln|csc(x)cot(x)|+c r cos(x)dx =sin(x)+c r sec(x)dx =ln|sec(x)+tan(x)|+c r tan(x)dx =ln|sec(x)|+c r cot(x)dx =ln|sin(x)|+c power reduction formulas inverse trig integrals r sinn(x)=1 n sin n1(x)cos(x)+n 1 n r sinn2(x)dx r sin1(x)dx = xsin1(x)+ p 1x2 +c r cosn(x)=1 n cos n 1(x)sin(x)+n 1 n r cosn 2(x)dx. These allow the integrand to be written in an alternative form which may be more amenable to integration. Z sin5(x)dx = z h 1 cos2(x) i 2 sin(x)dx = z h 1 u2 i 2 du = z h 1 2u2 +u4 i du = u 2 3 u3 + 1 5 u5 +c = cos(x)+ 2 3 cos3(x) 1 5 cos5(x)+c For the following, let u and v be functions of x, let n be an integer, and let a, c, and c be constants.
Convert the remaining factors to cos( )x (using sin 1 cos22x x.) 1.
If n= 1 exponential functions with base a: Let’s first notice that we could write the integral as follows, ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x. ∫ f dx + ∫ g dx: Trig cheat sheet definition of the trig functions right triangle definition for this definition we assume that 0 2 p <<q or 0°<q<°90.
Functions ∫sin cosxdx x= − ∫cos sinxdx x= − sin sin22 1 2 4 x ∫ xdx x= − cos sin22 1 2 4 x ∫ xdx x= + sin cos cos3 31 3 ∫ xdx x x= − cos sin sin3 31 3 ∫ xdx x x= − ln tan sin 2 dx x xdx x ∫ = ln tan cos 2 4 dx x xdx x π = + ∫ 2 cot sin dx xdx x x ∫ = − 2 tan cos dx xdx x x ∫ = 3 2 cos 1 ln tan sin 2sin 2 2 dx x x x x
Some of the following trigonometry identities may be needed. The following is a list of integrals (antiderivative functions) of trigonometric functions.for antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions.for a complete list of antiderivative functions, see lists of integrals.for the special antiderivatives involving trigonometric functions, see trigonometric integral. Integral rules of trigonometric functions. Opposite sin hypotenuse q= hypotenuse csc opposite q= adjacent cos hypotenuse q= hypotenuse sec adjacent q= opposite tan adjacent q= adjacent cot opposite q= unit circle definition for this definition q is any angle.
In integral calculus, the trigonometric functions are involved in integration but the integrals of trigonometric functions cannot be evaluated directly and it requires some special rules to find the integrals of them.
8.5 integrals of trigonometric functions 597 solution. The integration formulas for inverse trigonometric functions can be disguised in many ways. Unfortunately, this is not typical. Xn+1 n+ 1 + c;
Z ax dx= ax ln(a) + c with base e, this becomes: