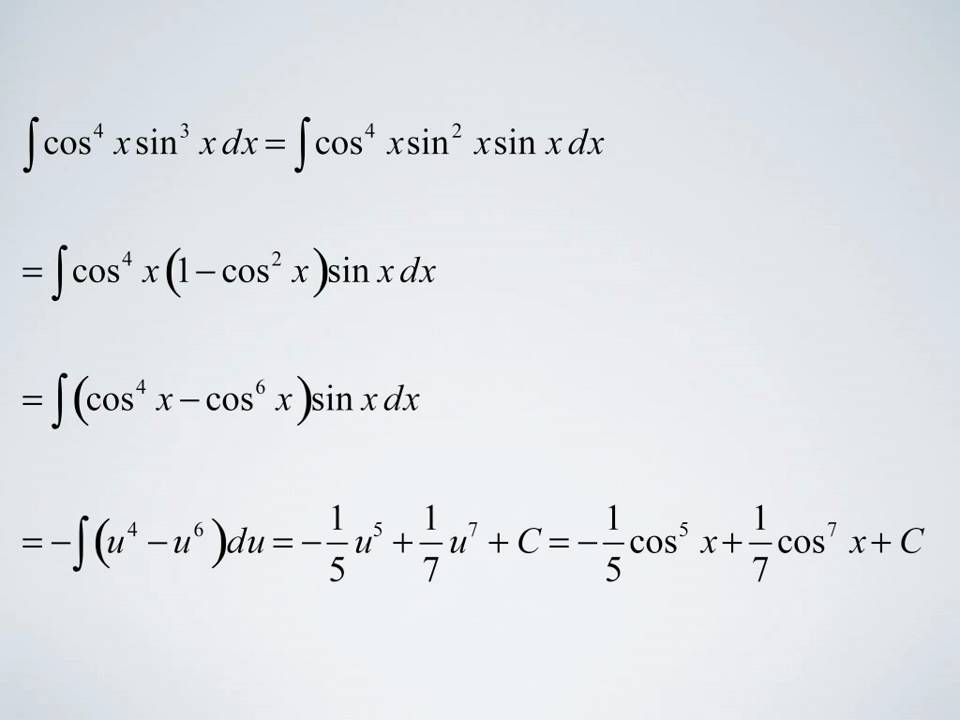It is assumed that you are familiar with the following rules of differentiation. Sin 1 y q==y 1 csc y q= For a complete list of.
basicintegral Images Frompo 1
Z sin(2x)cos(5x) dx here, we use the sum formulas:
∫sec x dx = ln|tan x + sec x| + c.
The following are some standard trigonometric integration formulas with proofs. ∫e x dx = e x + c; In the video, we work out the antiderivatives of the four remaining trig functions. Integrals involving sec(x) and tan(x):
When calculating integrals of inverse trig functions, we use integration by parts,.
Sin( )cos( ) = 1 2 (sin( + ) + sin( )) doing a similar thing to the cos formula, one gets rules that will help for integrals of the form cos( )cos( ) and sin( )sin( ). The important rules for integration are: We need to memorize 10 trig integrals, but what if there were an easier way? Integral rules of trigonometric functions.
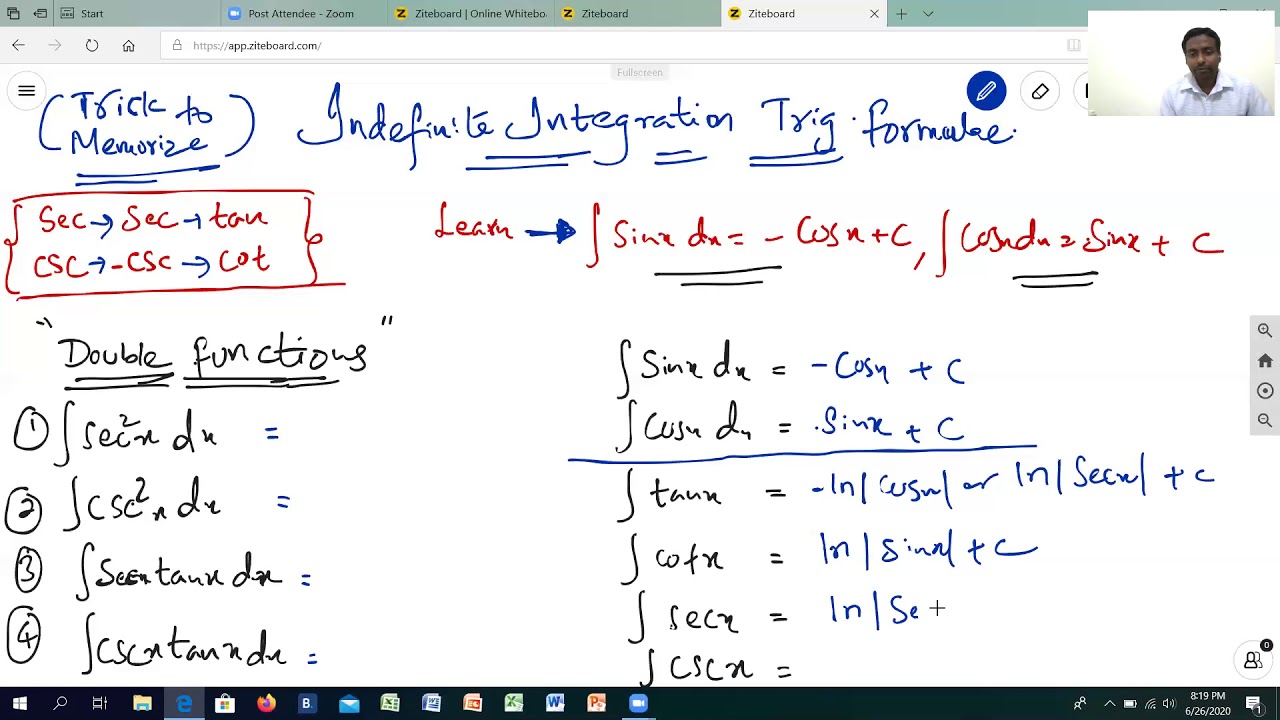
Here are some hints to help you remember the trig differentiation and integration rules:
∫cos(x) dx = sin(x) + c; If n6= 1 lnjxj+ c; Examples of such expressions are. Dx= ln( 1 x+ a (5) z (x+ a)ndx= (x+ a)n+1.
The different rules for integration of exponential functions are:
∫cos x dx = sin x + c. In the past, we’ve learned how inverse trigonometric functions can help us find unknown angles. Opposite sin hypotenuse q= hypotenuse csc opposite q= adjacent cos hypotenuse q= hypotenuse sec adjacent q= opposite tan adjacent q= adjacent cot opposite q= unit circle definition for this definition q is any angle. If n= 1 exponential functions with base a:
Let’s first notice that we could write the integral as follows, ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x.
Trigonometric integrals r sin(x)dx = cos(x)+c r csc(x)dx =ln|csc(x)cot(x)|+c r cos(x)dx =sin(x)+c r sec(x)dx =ln|sec(x)+tan(x)|+c r tan(x)dx =ln|sec(x)|+c r cot(x)dx =ln|sin(x)|+c power reduction formulas inverse trig integrals r sinn(x)=1 n sin n1(x)cos(x)+n 1 n r sinn2(x)dx r sin1(x)dx = xsin1(x)+ p 1x2 +c r cosn(x)=1 n cos n 1(x)sin(x)+n 1 n r cosn 2(x)dx. When the trig functions start with “ c ”, the differentiation or integration is negative (cos and csc). The antiderivatives of tangent and cotangent are easy to compute,. In integral calculus, the trigonometric functions are involved in integration but the integrals of trigonometric functions cannot be evaluated directly and it requires some special rules to find the integrals of them.
Below are the list of few formulas for the integration of trigonometric functions:
Now recall the trig identity, cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x. ∫sec 2 (x) dx = tan(x) + c; We have a table of integrals, but it’s hard to keep track of what means what. Adding the two, one gets:
Z ex dx= ex + c if we have base eand a linear function in the exponent, then z eax+b dx= 1 a eax+b + c trigonometric functions z sin(x)dx= cos(x) + c z
These lead directly to the following indefinite integrals. If the power of the sine is odd and positive: ∫tan x dx = ln|sec x| + c. Sometimes, there are things you need to memorize.
On occasions a trigonometric substitution will enable an integral to be evaluated.
Integration using trig identities or a trig substitution some integrals involving trigonometric functions can be evaluated by using the trigonometric identities. The following integration problems use the method of trigonometric (trig) substitution. These formulas are meant to simplify the tough calculations of calculus with the utmost ease and this is the reason why every student starts with all basic formulas of integration. Integrals of trigonometric functions ∫sin cosxdx x c= − + ∫cos sinxdx x c= + ∫tan ln secxdx x c= + ∫sec ln tan secxdx x x c= + + sin sin cos2 1( ) 2 ∫ xdx x x x c= − + cos sin cos2 1 ( ) 2 ∫ xdx x x x c= + + ∫tan tan2 xdx x x c= − + ∫sec tan2 xdx x c= + integrals of exponential and logarithmic functions ∫ln lnxdx x x x c= − + ( ) 1 1 2 ln ln 1 1
∫ln(x) dx = x ln(x) − x + c;
Integrals involving sin(x) and cos(x): Integrals resulting in inverse trig functions are normally challenging to integrate without the formulas derived from the derivative of inverse functions. Convert the remaining factors to cos( )x (using sin 1 cos22x x.) 1. Save a du x dx sin( ) ii.
X d x = sin.
For the functions other than sin and cos , there’s always either one tan and two secants , or one cot and two cosecants on either side of the formula. Depending upon your instructor, you may be expected to memorize these antiderivatives. ∫cot x dx = ln|sin x|. Integration rules and techniques antiderivatives of basic functions power rule (complete) z xn dx= 8 >> < >>:
These allow the integrand to be written in an alternative form which may be more amenable to integration.
Basic forms z xndx = 1 n+ 1 xn+1(1) z 1 x dx= lnjxj (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2. ∫a x dx = a x /ln(a) + c; Trig cheat sheet definition of the trig functions right triangle definition for this definition we assume that 0 2 p <<q or 0°<q<°90. Integral formula for trig identities if you are a mathmatics students then you can easily get the significance of integration formulas.
Tricks to memorize trig integrals.
We can use and rearrange double angle identities, such as when given a squared trig function. It is a method for finding antiderivatives of functions which contain square roots of quadratic expressions or rational powers of the form n 2 (where n is an integer) of quadratic expressions. We can use the chain rule when the variable in brackets is more complex than x, for example , as we have divided by the derivative of the brackets. The method of trig substitution may be called upon when.
For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions.