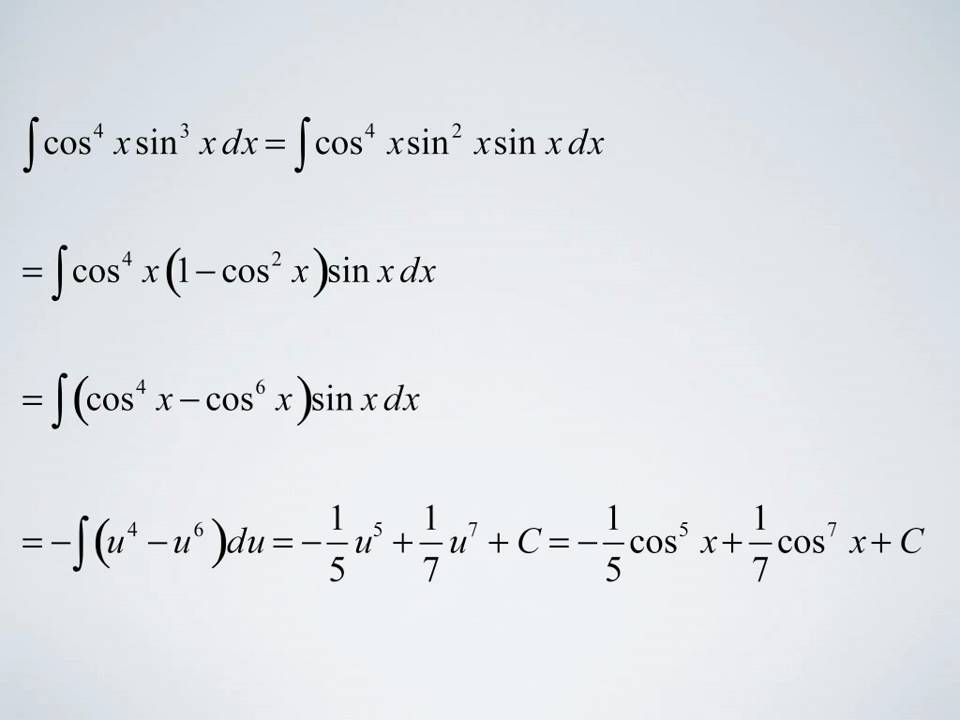X 9 x 4 3 f, x 2, technology with definite integrals such as the one given in example 5, remember that you can resort to a numerical simpson’s rule (with ) to the integral in the example, you obtain It is assumed that you are familiar with the following rules of differentiation. ∫cos x dx = sin x + c.
Core 4 Integrating Trigonometric Functions 1
If n6= 1 lnjxj+ c;
If n= 1 exponential functions with base a:
Ln | sec x + tan x | + c: Integrals of the form $\int \sin^m x \cdot \cos^n x dx$ case 1: X 9 x 4 3, f x 2, technology with definite integrals such as the one given in example 5, remember that you can resort to a numerical simpson’s rule (with ) to the integral in the example, For a complete list of.
In a simple straight language integration can be defined as the measure, which basically assigns numbers to the several functions.the numbers are basically assigned which may describe the displacement,volume or area etc of such concerned function.
Xn+1 n+ 1 + c; We rst need to review the derivative rules for trigonometric functions. A definite integral is used to compute the area under the curve these are some of the most frequently encountered rules for differentiation and integration. Integrals of exponential and trigonometric functions.
An integral of the form:
Below are the list of few formulas for the integration of trigonometric functions: Cos((a b)x) a b +c the other integrals of products of sine and cosine follow similarly. Let’s first notice that we could write the integral as follows, ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x. An indefinite integral computes the family of functions that are the antiderivative.
For the following, let u and v be functions of x, let n be an integer, and let a, c, and c be constants.
$m$ is an odd integer : For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions. In integral calculus, the trigonometric functions are involved in integration but the integrals of trigonometric functions cannot be evaluated directly and it requires some special rules to find the integrals of them. Ln | sin x | + c:
These lead directly to the following indefinite integrals.
Now recall the trig identity, cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x. We've got the integral of a polynomial in u, which can readily be found. Apr 04, 22 09:19 am. ∫ cos m x cos n x d x or ∫ sin m x sin n x d x or ∫ sin m x cos n x d x.
There are two which are the most important and come up the most:
X d x = − cos. Integral rules of trigonometric functions. ∫sec x dx = ln|tan x + sec x| + c. Similarly, if n is odd, then the substitution u = sin x can be utilized.
Cos(ax)cos(bx)dx = 1 2 sin((a b)x) a b + sin((a+b)x) a+b +c.
©2005 paul dawkins trig cheat sheet definition of the trig functions right triangle definition for this definition we assume that 0 2 p <<q or 0°<q<°90. Don't forget to return to the original variable x. The following are some standard trigonometric integration formulas with proofs. D dx sec(x) = sec(x)tan(x) d dx tan(x) = sec2(x) d dx csc(x) = csc(x)cot(x) d dx cot(x) = csc2(x) 2 ad hoc integration.
Both m and n are even.
1 2 sin((a+b)x)+sin((a b)x) dx = 1 2. Now, we'll investigate typical cases of trigonometric integrations. ∫ du a2+u2 = 1 a tan−1 u a +c ∫ d u a 2 + u 2 = 1 a tan − 1 u a + c. If a 6= b, then:
Since the derivative of ex is e x;e is an antiderivative of ex:thus z exdx= ex+ c recall that the exponential function.
Suppose our integration is of the form. ∫ du √a2−u2 = sin−1 u a +c ∫ d u a 2 − u 2 = sin − 1 u a + c. Z ex dx= ex + c if we have base eand a linear function in the exponent, then z eax+b dx= 1 a eax+b + c trigonometric functions z sin(x)dx= cos(x) + c z The following integration formulas yield inverse trigonometric functions:
Let sin x = t then, dt = cos x dx.
Z ax dx= ax ln(a) + c with base e, this becomes: Integration rules and techniques antiderivatives of basic functions power rule (complete) z xn dx= 8 >> < >>: Sin(ax)sin(bx)dx = 1 2 sin((a b)x) a b. The list of integral rules of trigonometric functions with proofs.
X /2 + sin (2 x)/4 + c = (x + sin x ∙ cos x)/2 + c:
∫ du u√u2−a2 = 1 a sec−1 u a +c ∫ d u u u 2 − a 2 = 1 a sec − 1 u a + c. X d x = sin. In integration we basically take the infinitesimal. ∫tan x dx = ln|sec x| + c.
\begin {array} {c}&\int \cos mx \cos nx \, dx &\text {or} &\int \sin mx \sin nx \,.
Apr 04, 22 09:25 am. ∫cot x dx = ln|sin x|.