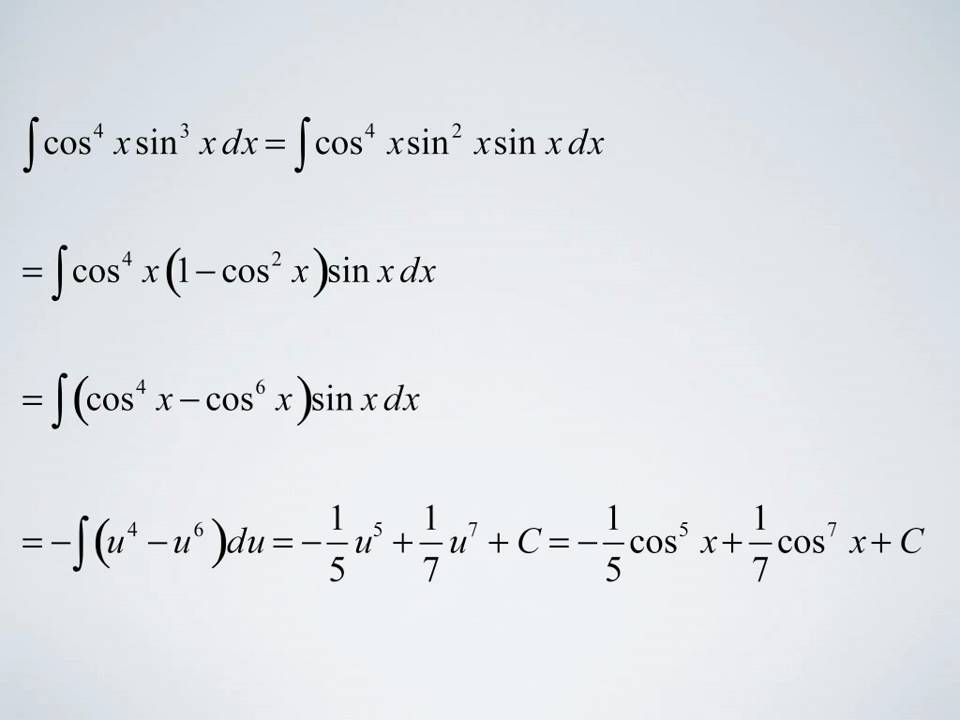8.5 integrals of trigonometric functions 597 solution. Here are some hints to help you remember the trig differentiation and integration rules: In integration we basically take the infinitesimal data as the combination.
PPT Inverse Trigonometry Integrals PowerPoint
For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions.
Or, you could rewrite the integrand only in terms of a single trigonometric function.
X d x = sin. E.) f.) so that ; The following are some standard trigonometric integration formulas with proofs. We rst need to review the derivative rules for trigonometric functions.
We can use and rearrange double angle identities, such as when given a squared trig function.
Ln | sin x | + c: For the following, let u and v be functions of x, let n be an integer, and let a, c, and c be constants. Integrals resulting in inverse trig functions are normally challenging to integrate without the formulas derived from the derivative of inverse functions. In each pair, the derivative of one function is the negative of the other.
If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions.
∫sec x dx = ln|tan x + sec x| + c; 16 x2 49 x2 dx ∫ − 22 x = ⇒ =33sinθ dx dcosθθ Rules for integrals of odd functions. In a simple straight language integration can be defined as the measure, which basically assigns numbers to the several functions.the numbers are basically assigned which may describe the displacement,volume or area etc of such concerned function.
Sets found in the same folder.
Generally, if the function is any trigonometric function, and is its derivative, in all formulas the constant a is assumed to be nonzero, and c denotes the. For a complete list of antiderivative functions, see lists of integrals. Review the basic integration rules involving elementary functions. Some of the following trigonometry identities may be needed.
Integrals involving inverse trigonometric functions the derivatives of the six inverse trigonometric functions fall into three pairs.
\cos^ {2} x = \frac { 1+ \cos 2x} {2} cos2 x = 21+cos2x. 2 22 a sin b a bx x− ⇒= θ cos 1 sin22θθ= − 22 2 a sec b bx a x− ⇒= θ tan sec 122θθ= − 2 22 a tan b a bx x+ ⇒= θ sec 1 tan2 2θθ= + ex. The antiderivatives of tangent and cotangent are easy to compute, but not so much secant and cosecant. Recall the definitions of the trigonometric functions.
Integral rules of trigonometric functions.
X /2 + sin (2 x)/4 + c = (x + sin x ∙ cos x)/2 + c: Let’s first notice that we could write the integral as follows, ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x. For example, and when listing the antiderivative that corresponds to each of the inverse trigonometric functions,. Integration is used to find many useful parameters or quantities like area, volumes, central points, etc., on a large scale.
Sin 2 x = 1 − cos 2 x 2.
The most common application of integration is to find the area under the curve on a graph of a function. ∫sec 2 x dx = tan x + c Z sin5(x)dx = z h 1 cos2(x) i 2 sin(x)dx = z h 1 u2 i 2 du = z h 1 2u2 +u4 i du = u 2 3 u3 + 1 5 u5 +c = cos(x)+ 2 3 cos3(x) 1 5 cos5(x)+c An indefinite integral computes the family of functions that are the antiderivative.
$m$ is an odd integer :
In the past, we’ve learned how inverse trigonometric functions can help us find unknown angles. Below are the list of few formulas for the integration of trigonometric functions: ∫cos x dx = sin x + c; Sometimes we can work out an integral, because we know a matching derivative.
Integration of trigonometric functions formulas.
Trigonometric integrals r sin(x)dx = cos(x)+c r csc(x)dx =ln|csc(x)cot(x)|+c r cos(x)dx =sin(x)+c r sec(x)dx =ln|sec(x)+tan(x)|+c r tan(x)dx =ln|sec(x)|+c r cot(x)dx =ln|sin(x)|+c power reduction formulas inverse trig integrals r sinn(x)=1 n sin n1(x)cos(x)+n 1 n r sinn2(x)dx r sin1(x)dx = xsin1(x)+ p 1x2 +c r cosn(x)=1 n cos n 1(x)sin(x)+n 1 n r cosn 2(x)dx. Depending upon your instructor, you may be expected to memorize these antiderivatives. First split off one power of sine, writing: Now recall the trig identity, cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x.
Cos 2 x = 1 + cos 2 x 2.
Sin5(x) = sin4(x)sin(x) = h sin2(x) i 2 sin(x) = h 1 cos2(x) i 2 sin(x) and then integrate, using the substitution u = cos(x) )du = sin(x)dx: D dx sin(x) = cos(x) d dx cos(x) = sin(x) but also: Integrals of the form $\int \sin^m x \cdot \cos^n x dx$ case 1: For the functions other than sin and cos , there’s always either one tan and two secants , or one cot and two cosecants on either side of the formula.
When calculating integrals of inverse.
There are two which are the most important and come up the most: You could utilize the following identities: ∫tan x dx = ln|sec x| + c; ∫cot x dx = ln|sin x| + c;
D dx sec(x) = sec(x)tan(x) d dx tan(x) = sec2(x) d dx csc(x) = csc(x)cot(x) d dx cot(x) = csc2(x) 2 ad hoc integration.
When the trig functions start with “ c ”, the differentiation or integration is negative (cos and csc). A definite integral is used to compute the area under the curve these are some of the most frequently encountered rules for differentiation and integration. A.) b.) c.) so that ; The first rule to know is that integrals and derivatives are opposites!.
In the video, we work out the antiderivatives of the four remaining trig functions.
To work out the integral of more complicated functions than just the known ones, we have some integration rules. In integral calculus, the trigonometric functions are involved in integration but the integrals of trigonometric functions cannot be evaluated directly and it requires some special rules to find the integrals of them.