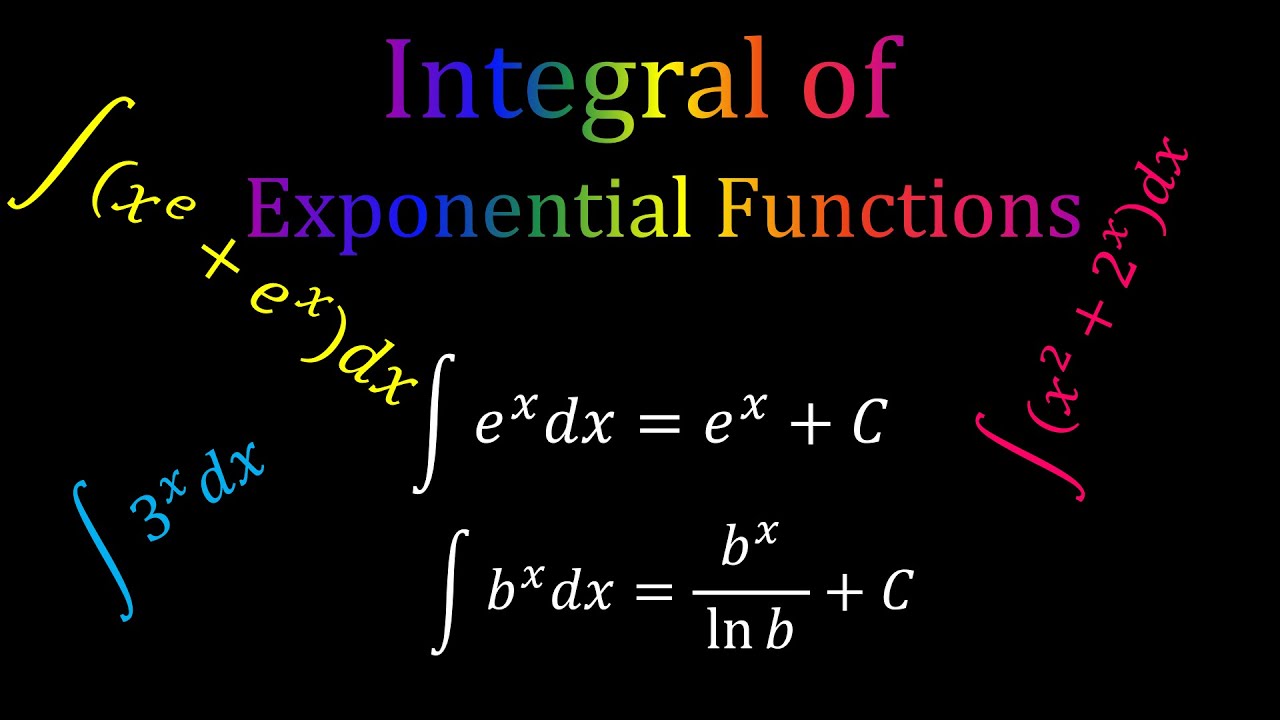Z ex dx= ex + c if we have base eand a linear function in the exponent, then z eax+b dx= 1 a eax+b + c trigonometric functions z sin(x)dx= cos(x) + c z A definite integral is used to compute the area under the curve these are some of the most frequently encountered rules for differentiation and integration. Use implicit differentiation to find dy/dx given e x yxy 2210 example:
Integration Rules for Exponential Functions YouTube
Nearly all of these integrals come down to two basic formulas:
A − n = 1 a n = 1 a × 1 a ×.
N t i m e s. Xm × xn = xm + n. The integral of the exponential function is given by the following formula $\displaystyle \int a^xdx=\frac{a^x}{\ln(a)}$, where $a > 0$ and $a \neq 1$ $e^u$ intermediate steps ∫ (f + g) dx:
Pay special attention to what terms the exponent applies to.
Integration rules and techniques antiderivatives of basic functions power rule (complete) z xn dx= 8 >> < >>: \[f(x) = a.x^{\frac{m}{n}}\] we can therefore use the power rule for integration to integrate any function looking like \(f(x)=a.\sqrt[n]{x^m}\). ∫ e x d x = e x + c , ∫ a x d x = ln ( a ) a x + c. Warm up evaluate each expression for the given values of the variables.
Observe the following decreasing pattern:
X n+1 n+1 + c: First, multiply the exponential functions together. `int e^udu=e^u+k` it is remarkable because the integral is the same as the expression we started with. ∫ f dx + ∫ g dx:
Use the substitution u= 3x+ 1 )du= 3dx)du 3 = dx:the integral becomes r 2udu 3 = 1 3 r 2u du:the integrand 2u is now simple and you can integrate it using the formula for integral of ax with a= 2:obtain 1 3 z 2udu= 1 3 1 ln2 2u+ c= 1 3ln2 23x+1 + c:
Xm ÷ xn = xm − n. In this article, we’ll master the techniques needed in integrating exponential functions.we’ve learned that exponential functions are essential in modeling population growth, cell growth, radioactive decay, and other significant applications. You have seen positive exponents. \int e^x\, dx = e^x + c, \quad \int a^x\, dx = \frac{a^x}{\ln(a)} +c.
Remember the three general rules for integration 1.
1) ∫x−1 dx ln x + c 2) ∫3x−1 dx 3ln x + c 3) ∫− 1 x dx −ln x + c 4) ∫ 1 x dx ln x + c 5) ∫−e x dx −ex + c 6) ∫ex dx ex + c 7) ∫2 ⋅ 3x dx 2 ⋅ 3x ln 3 + c 8) ∫3 ⋅ 5x dx 3 ⋅ 5x ln 5 + c ∫ e x d x = e x + c , ∫ a x d x = a x ln ( a ) + c. By reversing the process in obtaining the derivative of the exponential function, we obtain the remarkable result: Integral of ex:obtain 1 2 z e udu= 1 2 e + c= 1 2 ex2+1 + c:
As you do the following problems, remember these three general rules for integration :
Find the integral r 23x+1 dx: These formulas lead immediately to the following indefinite integrals : F x e x3 ln , 1,0 example: Multiply two numbers with exponents by adding the exponents together:
If n6= 1 lnjxj+ c;
Power rule (n≠−1) ∫ x n dx: Fractional exponents functions looking like \(f(x) = a.\sqrt[n]{x^m}\) can be written as powers of \(x\) using fractional exponents: Click here to return to the list of problems. An indefinite integral computes the family of functions that are the antiderivative.
(recall that and.) (use the properties of integrals.) (use formula 3 from the introduction to this section on integrating exponential functions.).
Use the rule above and rewrite this integral with exponents. , where a is any positive constant not equal to 1 and is the natural (base e) logarithm of a. Z ax dx= ax ln(a) + c with base e, this becomes: For the following, let u and v be functions of x, let n be an integer, and let a, c, and c be constants.
In the following formulas, erf is the error function and ei is the exponential integral.
Xn+1 n+ 1 + c; Nearly all of these integrals come down to two basic formulas: Divide two numbers with exponents by subtracting one exponent from the other: Exponential functions occur frequently in physical sciences, so it can be very helpful to be able to integrate them.
If n= 1 exponential functions with base a:
Exponential functions occur frequently in physical sciences, so it can be very helpful to be able to integrate them. ∫ e x d x = e x + c , ∫ a x d x = a x ln ( a ) + c. When an exponent is raised to a power, multiply the exponents together: