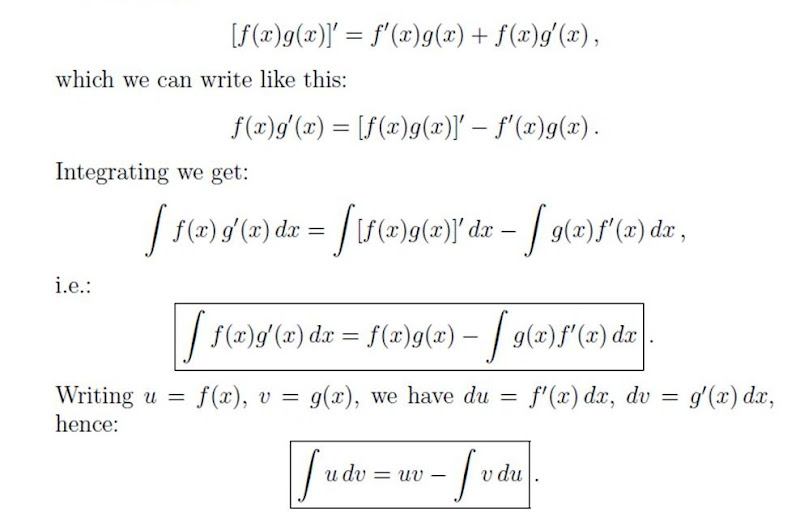∫ u d v = u v. Integrating both sides and solving for one of the integrals leads to our integration by parts formula: In class xii, its weightage is 35 marks.
Integration by parts formula Calculus, Integration by
Integration by part is a little complex rule.
In class x, its weightage is nominal marks.
The di culty of integration by parts is in choosing u(x) and v0(x) correctly. Z udv= uv z vdu integration by parts (which i may abbreviate as ibp or ibp) \undoes the product rule. So, we are going to begin by recalling the product rule. What is integration by parts?
This unit derives and illustrates this rule with a number of examples.
It is derived from the product rule of differentiation. In a way, it’s very similar to the product rule, which allowed you to find the derivative for two multiplied functions. With the product rule, you labeled one function “f”, the other “g”, and then. The second one is that you can use the limit as you are going with integrals of functions.
The first one is that you can apply limits after the end of your integrating result as you did in indefinite.
If you are using the first method then make sure first you. U is the function u(x) v is the function v(x) u' is the derivative of the function u(x) The integration by parts formula is. It is usually the last resort when we are trying to solve an integral.
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative.
Integration by parts is what you use when you want to integrate the product of two functions. Let f (x)=lnx and g' (x)= x 5 , then f' (x)= 1 x and g (x)= x 6 6. The method integration by parts is known to be a special method of integration that is often useful. ∫u v dx equals u∫v dx −∫u' (∫v dx) dx.
By using this website, you agree to our cookie policy.
It can be applied when two functions are in multiplication. Let’s derive the equation for integration by parts. ∫ x 5 ln in x dx = ∫ ln in x x 5 dx. ∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u.
When the integrand function is represented as a product of two or more functions, integrating the given function can be done using the integration by parts rule.
The liate rule is a rule of thumb that tells you which function you should choose as u(x): U is the function u(x) is the formula for integration by parts. Observation more information integration by parts essentially reverses the product rule for differentiation applied to (or ).: (ab)’ = ab’ + a’b.
The product rule for derivatives is what you use when you want to differentiate the product of two functions.
Integration by parts is used to integrate when you have a product (multiplication) of two functions. Integration by parts comes under section “calculus”. We use it when two functions are multiplied together, but are also helpful in many other ways. The substitution u gx= ( )will convert (( )) ( ) ( ) ( ) b gb( ) a ga ∫∫f g x g x dx f u du= using du g x dx= ′( ).
23 ( ) 2 1.
Standard integration techniques note that at many schools all but the substitution rule tend to be taught in a calculus ii class. In class xi, its weightage is 5 marks. Liate the word itself tells you in which order of priority you should use u(x). ∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx.
Using the fact that integration reverses differentiation we'll arrive at a formula for integrals, called the integration.
Integration by parts, definite integrals. Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways. I recommended to you to. Applying the product rule to solve integrals.
When choosing uand dv, we want a uthat will become simpler (or at least no more complicated) when we
Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point. The idea it is based on is very simple: Integration by parts is a fancy technique for solving integrals. For example, you would use integration by parts for ∫x · ln(x) or ∫ xe 5x.
Let us see the rule of integration by parts:
For indefinite integrals drop the limits of integration. ∫(ab)’.dx = ∫ab’.dx + ∫a’b.dx It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more. Apply integration by parts formula, we have.
Discover more science & math facts & information.