$$\int\left( \sqrt{\tan x}+\sqrt{\cot x}\right)dx$$ stack exchange network stack exchange network consists of 178 q&a communities including stack overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. We take, (t + 1 t) = v ⇒ (1 − 1 t2)dt = dv,&,t2 + 1 t2 = v2 − 2. Integral from 0 to pi 2 root cot x root cot x root tan x dx.
Example 41 Evaluate integral [root cot x + root tan x] dx
Im gonna give u the solution and i hope it is the easiest, regardless of the fact that it could be a bit lengthy.
I=∫ 0 2π ( tanx + cotx )dx i=∫ 0 2π ( cosxsinx + sinxcosx )dx i=∫ 0 2π ( sinxcosx sinx+cosx )dx letz=sinx−cosx,dz=(cosx+sinx)dx z 2=sin 2x+cos 2x−2sinxcosx z 2=1−2sinxcosx 2sinxcosx=1−z 2 sinxcosx= 21−z 2 when,x=0,t=−1;x= 2π ,t=1 i=∫ −11.
The answer is =2sqrt(tanx)+c we need tanx=sinx/cosx sinx=cosxtanx=tanx/secx therefore, the integral is i=int(sqrt(tanx)dx)/(sinxcosx)=int(sqrt(tanx)dx)/(tanx/secx*1/secx) =int(sec^2xdx)/sqrt(tanx) let u=tanx, =>, du=sec^2xdx the integral is i=int(du)sqrt(u) =sqrt(u)/(1/2) =2sqrt(u) =2sqrt(tanx)+c = 2 ∫ t 2 + 1 t 4 + 1 d t. ∴ i 1 = ∫ 1 u2 + (√2)2 du = 1 √2 arctan( u √2). Dx = 2tdt sec2x = 2tdt 1 + tan2x = 2tdt 1 + t4.
Integral of 0 to pi/2 root (cot x) / root( cotx)+root (tan x) dx get the answers you need, now!
Integral from 0 to π/2 (√cot x) / [(√cot x + √tan x)] dx = login. Click here👆to get an answer to your question ️ int^ (√(tanx)+√(cotx))dx = I hope it works out for you… thank you. Ncert solutions for class 12 physics;
I = ∫ ( cot x + tan x) d x.
Ncert solutions for class 12. = ∫ ( tan x ( 1 + cot x)) d x. (2) change into sec2x, as derivative of tan x is sec2. L e t tan x = t 2.
T − 1 t = u ⇒ (1 + 1 t2)dt = du,&,t2 + 1 t2 = u2 +2.
Ncert solutions for class 12 chemistry; T h e n, i = ∫ 0 π 4 ( sin. ⇒ d x = 2 t d t 1 + t 4. Hence, where, i 1 = ∫ 1 + 1 t2 t2 + 1 t2 dt.
∴ i = ∫ t ( 1 + 1 t 2) × 2 t 1 + t 4 d t.
Sec 2 x d x = 2 t d t. Find integral of root tan x. L e t i = ∫ 0 π 4 ( tan.
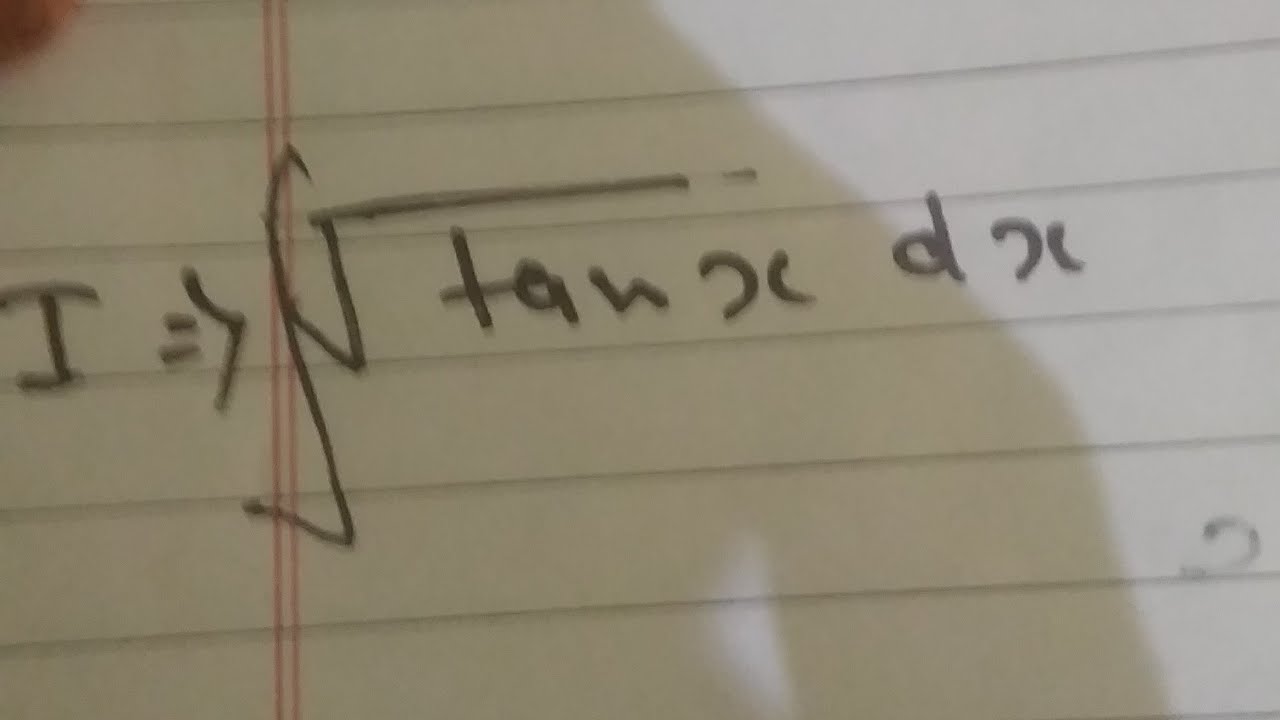

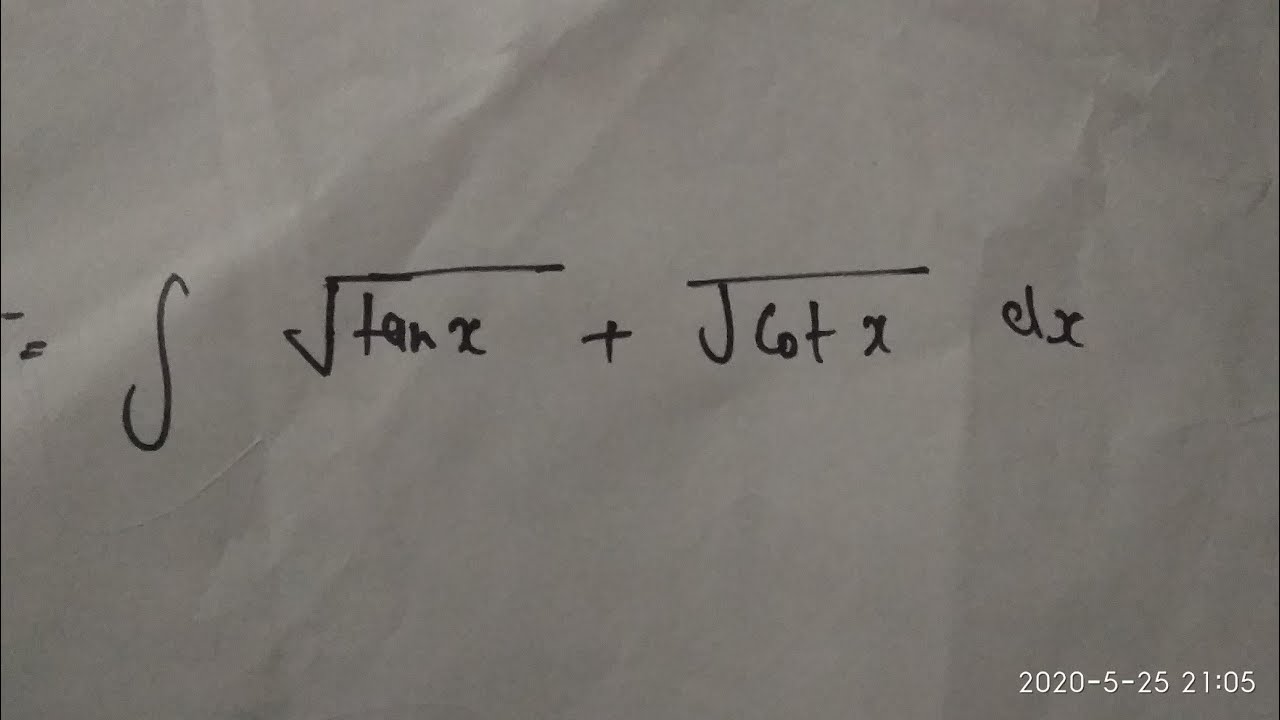

![Example 41 Evaluate integral [root cot x + root tan x] dx](https://i2.wp.com/d1avenlh0i1xmr.cloudfront.net/medium/be59389e-4f6e-4535-89d8-51262f85f2d7/slide36.jpg)