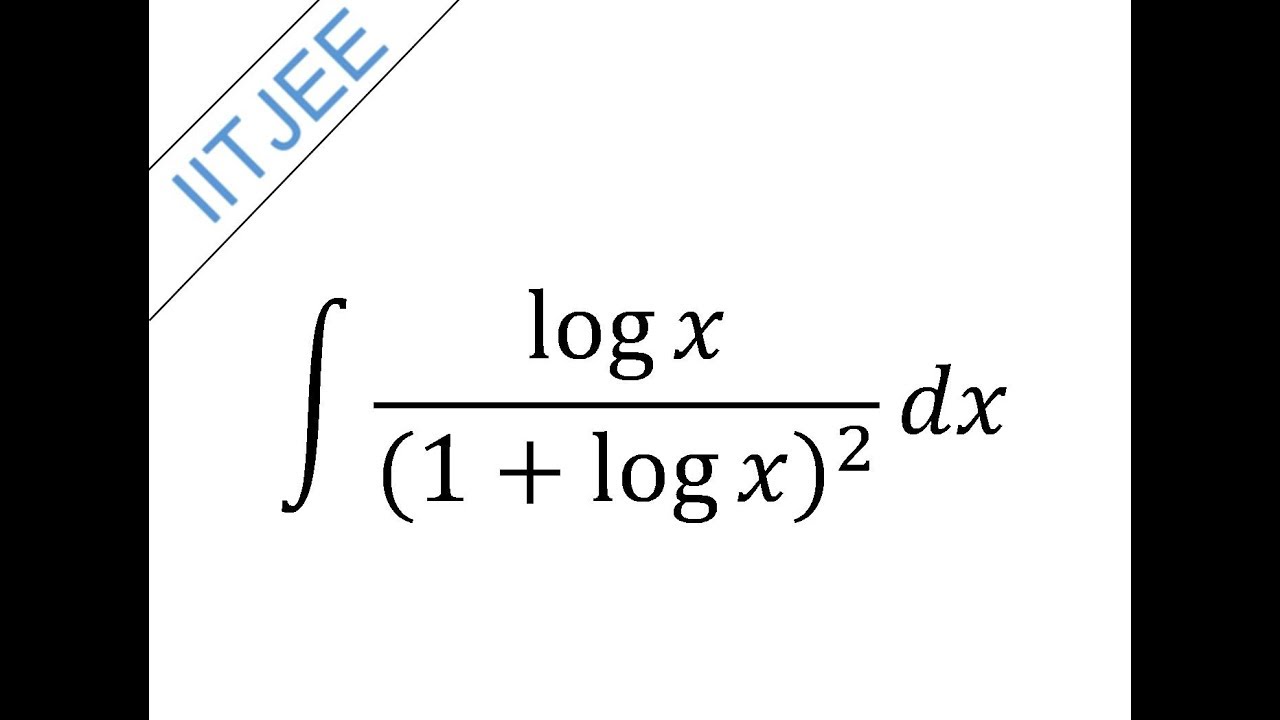D x = l o g x. ∴ ∫ ( log x) 2. Where c is the integration constant.
Example 36 Integration of log (sin x) from 0 to pi/2
Put log x = t.
Now substitude the value of logx as t and dx as x.dt.
∫ d x − ∫ (x 1. (if not, insert ln10 where needed.) int cos(log(x))dx = int xcos(log(x))*1/xdx let u=x and dv is the rest of the integrand. Take first function as log x, second function as 1. We have, i = \ (\int\) x log x dx.
The task is actually very simple with the help of integration by parts, but it requires a little trick.
Let [math]let t = u^2 => 2u.du = dt => u.du = dt /2 \\[/math] use integration by parts : L o g e (e x ) + c Where log x is the first function and 1 is the second function according to ilate rule. Ex 7.11, 8 by using the properties of definite integrals, evaluate the integrals :
Take log x = t.
Integral of log (x) \square! [l o g e x − l o g e e] + c = x. As you can see, there is only one function in $$ ∫ \ln(x)\,dx\,, $$ but integration by parts requires two. ∴ d 1 x d x = dt.
L o g e x − x + c x.
∴ i = t dt t dt ∫ log t dt = ∫ log t ⋅ 1 dt. By using integration by parts, and taking log x as first function and x as second function. Use integration by parts and solve. We follow the following steps.
For finding integration of lnx (log x), we use integration by parts.
Write ∫ log x dx = ∫ (log x). Now we can integrate v = int cos(log(x))*1/xdx = sin(log(x)) (use substitution with w=log(x)) parts gives us: The following formulas of integration and differentiation will be applied to evaluate the given integral: Share it on facebook twitter email.
Answered jun 26, 2020 by siwani01 (50.6k points) selected jun 27, 2020 by vikram01.
Let v u = ( log x) 2, v = 1. I= ∫ log(1+x^2) dx applying integration by parts using liate for fixing ist function, i = log(1+x^2). Let i = d ∫ log ( log x) x d x. By the method of integration by parts we have, ∫ f ( x) g ( x) d x = f ( x) ∫ g ( x) d x − ∫ [ f ′ ( x) ∫ g ( x) d x] d x.
To calculate integral of log tan(x), let us put it in the math editor format :
We will use integration by parts formula to prove this, let i = \(\int\) log x.1 dx. Ilate (inverse, logarithmic, algebraic, trigonometric, exponent) Replace t with log x = log x. Where f is the first function and g is the second function.
How to solve this integral?
∫ d x) d x [integration by parts] (l o g x) x − ∫ (x 1 ) x. Your first 5 questions are on us! The x in denom will we cancelled by the x in numerator. In this video, we tried to solve the integral of x log(x) dx using integration by parts method.
Now you remained with logt.dt integrate this using integration by parts.
Drop your questions in the comments section below. ∫ uvdx = u∫ vdx−∫ (du dx ∫ vdx) dx [ this is the rule for integration by parts. ∫_0^(𝜋/4) log(1+tan𝑥 ) 𝑑𝑥 let i=∫_0^(𝜋/4) log〖 (1+tan𝑥 )〗 𝑑𝑥 ∴ i=∫_0^(𝜋/4) log[1+tan(𝜋/4−𝑥) ] 𝑑𝑥 i=∫_0^(𝜋/4) log[1+(tan 𝜋/4 −tan𝑥)/(1 +〖 tan〗 𝜋/4. V v v ∫ u.
Which is chosen based on the order for the selection of the first function:
Take log x = t. ∫(log x) 2 /x dx. The trick is to write $\ln(x)$ as $1⋅\ln(x)$ and then apply integration by parts by integrating the $1$ and differentiating the. We have to find the integration of log x.
∫ l o g x.