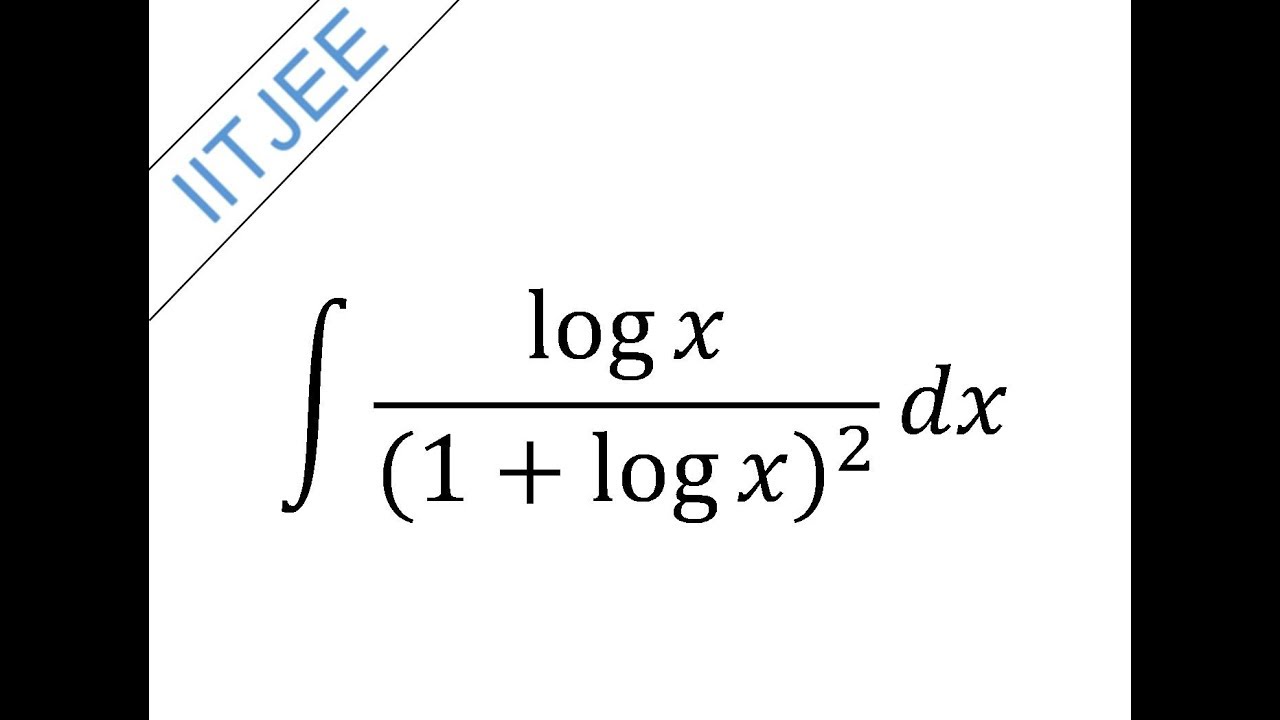Here nothing has been mentioned so, we will take the base of the log as e. For finding integration of lnx (log x), we use integration by parts. We will use integration by parts formula to prove this, let i = \(\int\) log x.1 dx.
The value of the integral `int_(0)^(1) x log sin ((pix)/(2
Where c is the integration constant.
∫_0^(𝜋/4) log(1+tan𝑥 ) 𝑑𝑥 let i=∫_0^(𝜋/4) log〖 (1+tan𝑥 )〗 𝑑𝑥 ∴ i=∫_0^(𝜋/4) log[1+tan(𝜋/4−𝑥) ] 𝑑𝑥 i=∫_0^(𝜋/4) log[1+(tan 𝜋/4 −tan𝑥)/(1 +〖 tan〗 𝜋/4.
1 xdx ∫ log x. We have, i = \ (\int\) x log x dx. Let us now explore its formula in the next section: D x = l o g x.
The trick is to write $\ln(x)$ as $1⋅\ln(x)$ and then apply integration by parts by integrating the $1$ and differentiating the logarithm:
Click here👆to get an answer to your question ️ int x log x dx = ? By using integration by parts, and taking log x as first function and x as second function. Share it on facebook twitter email. We have to find the integration of log x.
Answered jun 26, 2020 by siwani01 (50.6k points) selected jun 27, 2020 by vikram01.
= t log t − t + c. Stack exchange network consists of 179 q&a communities including stack overflow, the largest,. $\int_{0}^{1} \frac{\ln(x+1)}{x^2+1} dx$ i am a bit stuck here in evaluating the following integral:$$\int_{0}^{1}\frac{\log(1+x)}{1+x^2}\,\mathrm dx$$. ∫ l o g x.
Here are some examples illustrating how to ask for an integral.
(i will assume logx is natural log. Use integration by parts and solve. And as we know, from integration by parts, log x = u and x = v. Write ∫ log x dx = ∫ (log x).
Join / login >> class 12 >> maths >> integrals >> introduction and interpretation to integrals >> int x log x dx = ?
L o g e (e x ) + c The integration of log x gives the area under the curve f(x) = log x. ∫ d x − ∫ (x 1. [l o g e x − l o g e e] + c = x.
∫ d x) d x [integration by parts] (l o g x) x − ∫ (x 1 ) x.
Integrate 1/(cos(x)+2) from 0 to 2pi; Replace t with log x. ∴ i = t dt t dt ∫ log t dt = ∫ log t ⋅ 1 dt. To avoid ambiguous queries, make sure to use parentheses where necessary.
Take log x = t.
Put log x = t. Ex 7.11, 8 by using the properties of definite integrals, evaluate the integrals : Take first function as log x, second function as 1. Again by integrating the second term we get.
We follow the following steps.
Now we can integrate v = int cos(log(x))*1/xdx = sin(log(x)) (use substitution with w=log(x)) parts gives us: (if not, insert ln10 where needed.) int cos(log(x))dx = int xcos(log(x))*1/xdx let u=x and dv is the rest of the integrand. Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi; Integral of log (x) \square!
We have to simplify the expression ∫ x log x dx.
Let i = d ∫ log ( log x) x d x. L o g e x − x + c x. D x = l o g x. Integrate the integral of log x dx.
∴ d 1 x d x = dt.
Your first 5 questions are on us! Where log x is the first function and 1 is the second function according to ilate rule. Drop your questions in the comments section below. ∫(log x) 2 /x dx.
