∫ d x − ∫ (x 1. X) 3 3 + c. D x = l o g x.
What is the integral of log x/x? Quora
Now you remained with logt.dt integrate this using integration by parts.
L o g e x − x + c x.
Let log x = t. $\int_{0}^{1} \frac{\ln(x+1)}{x^2+1} dx$ i am a bit stuck here in evaluating the following integral:$$\int_{0}^{1}\frac. = t 3 3 + c. ⇒ 1 x d x = d t.
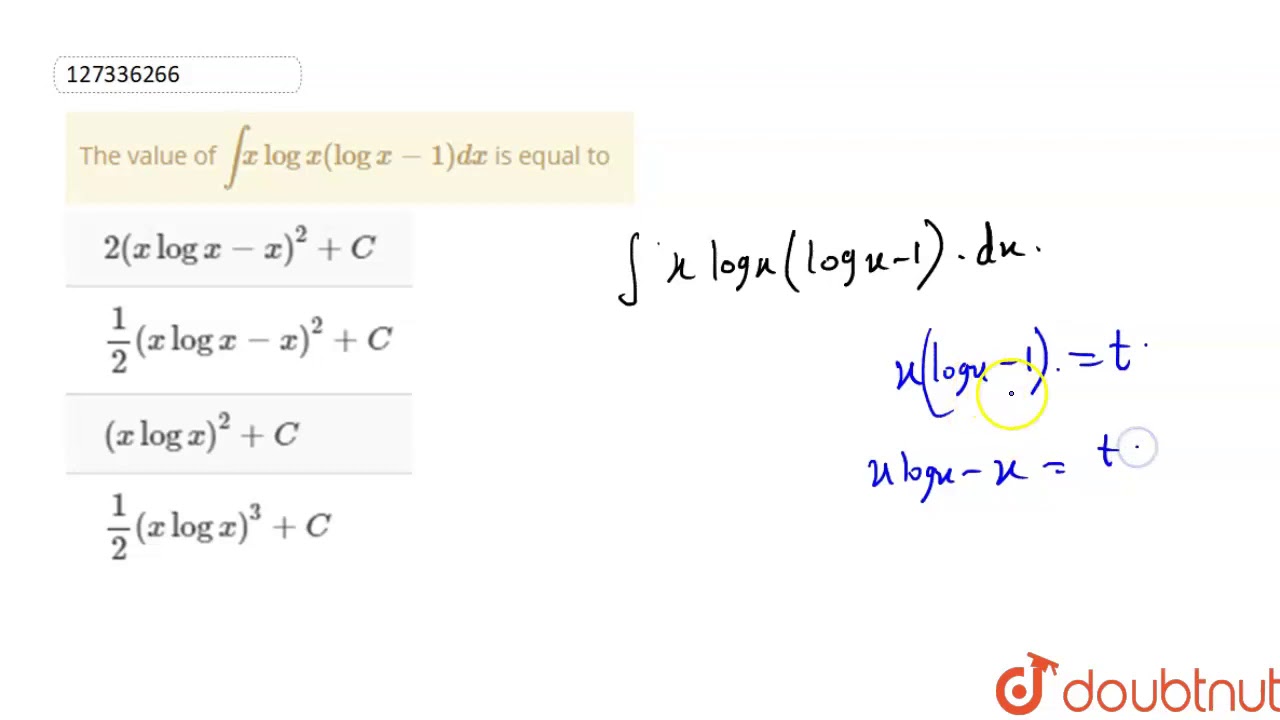
Let i let i = ∫ x sec.
Differenatiating with respect to x, we get. Buy now knockout jee main 2022 (one month) personalized ai tutor and adaptive time table, self study material, live classes, unlimited mock tests and personalized analysis reports, 24x7 doubt chat support,. Ex 7.11, 8 by using the properties of definite integrals, evaluate the integrals : ∫ l o g x.
Let log 𝑥= 𝑡 differentiate 𝑤.𝑟.𝑡.𝑥 𝑑𝑡/𝑑𝑥= 1/𝑥 𝑑𝑡.𝑥=𝑑𝑥 𝑑𝑥=𝑑𝑡.𝑥 step 2:
(a) π/4 (b) π/2 (c) 0 (d) π Putting x putting x 2 = t. Integrating function ∫1 (log𝑥 )^2/𝑥 𝑑𝑥 putting (𝑙𝑜𝑔𝑥 )^2=𝑡=𝑥 𝑑𝑡 = ∫1 𝑡^2/𝑥 𝑑𝑡.𝑥 = ∫1 〖𝑡^2 𝑑𝑡〗 = 𝑡^(2+1)/(2+1)+𝐶 = 𝑡. Let i = ∫ 3 2 x 3 (l o g x) 2 d x using, ∫ u.
V d x = u ∫ v d x − ∫ ( d x d u ∫ v d x ) d x i = 3 2 { ( l o g x ) 2 4 x 4 − ∫ 2 l o g x ⋅ x 1 4 x 4 d x }
Now we can integrate v = ∫cos(log(x)) ⋅ 1 x dx = sin(log(x)) (use substitution with w = log(x)) parts gives us: Where log x is the first function and 1 is the second function according to ilate rule. ∫_0^(𝜋/4) log(1+tan𝑥 ) 𝑑𝑥 let i=∫_0^(𝜋/4) log〖 (1+tan𝑥 )〗 𝑑𝑥 ∴ i=∫_0^(𝜋/4) log[1+tan(𝜋/4−𝑥) ] 𝑑𝑥 i=∫_0^(𝜋/4) log[1+(tan 𝜋/4 −tan𝑥)/(1 +〖 tan〗 𝜋/4. ∫cos(log(x))dx = xsin(log(x)) +xcos(log(x)) −∫cos(log(x))dx.
[l o g e x − l o g e e] + c = x.
What is the integration of log x whole square? The value of the integral ∫ log tan x dx x ∈ [0,π ⁄ 2] is equal to : Your first 5 questions are on us! Now, i = ∫ t 2 d t.
Put xx = t, then xx(1+logx)dx = dt.
Ex 7.2, 2 integrate the function: The x in denom will we cancelled by the x in numerator. L o g e (e x ) + c The integral ∫cos (logex)dx is equal to :
I = ∫ xx(1+log x)dx.
∫ d x) d x [integration by parts] (l o g x) x − ∫ (x 1 ) x. The integral ∫ cos( log x)dx is equal to: Since, this is a definite integral, to integrate it we have to use the following property of definite integrals. (2) x [cos (logex) + sin (logex)] + c.
Check out the video given below to know more about integration and antiderivative
∴ i = ∫ dt ⇒ i = t+ c ⇒ i = xx +c. Where c is the integration constant. What will be the intensity at a distance of 25 m from the source? We will use integration by parts formula to prove this, let i = \(\int\) log x.1 dx.
∴ i = 1 2 ∫ sec.
1 2 log (sec x2 + tan x2) + c. Dx ⇒ 2 x dx = d t. Do the same trick again to get. Dx ⇒ x dx = d t 2.
Integral of log (x) \square!