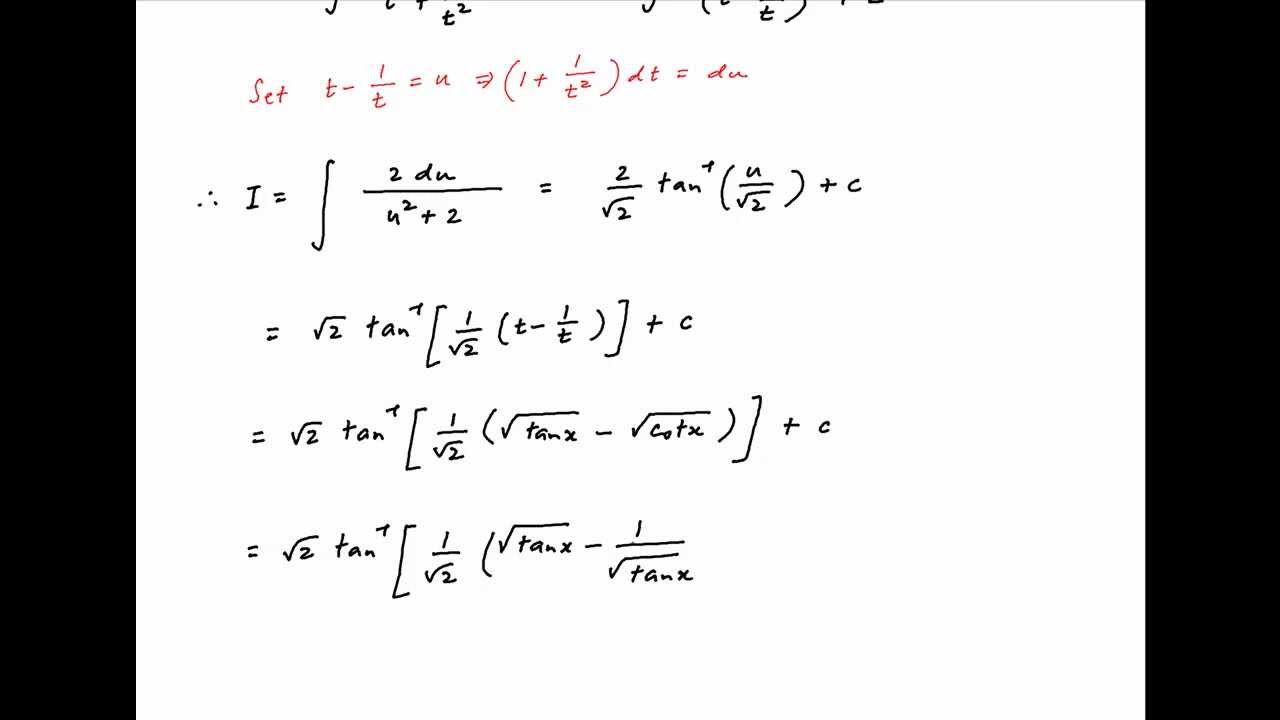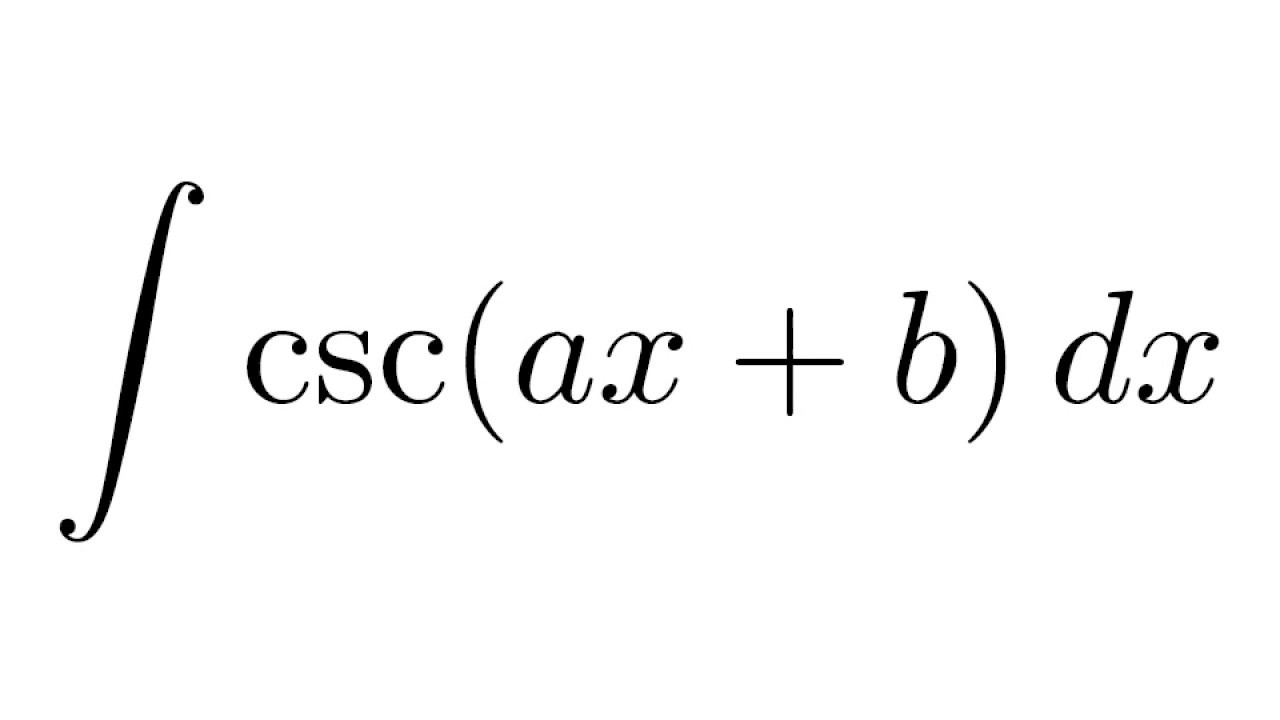The purpose of making this change will become apparent in the next two steps. X function with respect to x is written in the following mathematical form in integral calculus. I = ∫ cos 2 x d x.
Integration Of Cosec X DERIVATIVE TRIGONOMETRICAL
Hence, we get a new integration expression on the rhs, that means the same thing as the lhs.
U = cos x d u = − sin x d x d v = cos x sin 2 x d x v = − 1 sin x.
We rearrange it for du. As you know that cosec x = 1/sinx so cosec 2 x = 1/ sin 2 x. To integrate cot^2x, also written as ∫cot2x dx, cot squared x, (cot x)^2, and cot^2(x)we start by using standard trig identities to simplify the integral to a form we can work with. 1) cot x + (cot3 x / 3) + c.
What is the integration of cosec cube x?
= ∫( sin2x sinxcos2x −tan2x)dx. The indefinite integral of cosecant squared of angle x function with respect to x is equal to sum of the negative cotangent of angle x and a constant of integration. Ex 7.1, 19 sec 2 2 dx sec 2 2 = 1 cos 2 1 sin 2 = 1 cos 2 sin 2 1 = sin 2 cos 2 = tan 2 = sec 2 1 = sec 2 = ∫( sinx cos2x −sec2x + 1)dx.
In this tutorial we shall derive the integral of cosine squared x.
The cosecan integral can be deduced if you know some derivation formulas, then we will see how to get to the result of − log. Integrate by parts and simplify: X d x = − cot. The integration of secant squared of angle x function with respect to x is equal to sum of the.
We rearrange the pythagorean for cos2x so that we can substitute it into our previous trig identity.
Or, ∫ cosec x = l o g | t a n x 2 | + c. Edited may 27 '14 at 20:46. Where c is the integration constant. X d x = ∫ cosec 2.
Let us now go through the formula of the integration of tan square x.
We have multiple formulas for this. = ∫ cscx − 1 cot2x dx. We let u = tanx. Follow this answer to receive notifications.
Now we will divide both numerator and denominator by cos 2 x.
∫ 1 1 + cscx dx. This integral cannot be evaluated by the direct formula of integration, so using the trigonometric identity of half angle cos 2 x = 1 + cos. U) with the derivative formulas. = ∫ cscx −1 (cscx − 1)(cscx + 1) dx.
The integral of cosec x canbe determined by substitution method.
∫ cos 2 x sin 2 x d x + ∫ d x = − cos x sin x − ∫ − sin x − sin x d x + ∫ d x = − cot x + c. We will use trigonometric identities to find the integral of cosec^2x. As you can see, sec 2 x dx are the same terms in our integration problem, hence we can. Hence, we get a new expression for cosec squared x.
To start with this integral, there is a very powerful trick that allows us to solve it, we will multiply the csc.
Wait a moment and try again. To prove this formula, consider. Integration of cosecant squared of x is an important integral formula in integral calculus, and this integral belongs to the trigonometric formulae. = ∫ cscx −1 csc2x −1 dx.
The integration is of the form.
We can rewrite integration of cosec 2x as ∫cosec 2 x dx, or integral of cosec square x or cosec^2x or (cosec x) 2. Now, the square of the secant of angle x is written as sec 2. To find the integral of tan square x, we can use the trigonometric identities such as tan x = sin x/cos x and 1 + tan 2 x = sec 2 x. The integration of cosecant squared of x is of the form.
Then, du/dx = sec 2 x.
Integral of cos^2x=(1/2)(cosxsinx+x)+chere is why:here is one method: Where c is the integration constant. Integration of cos squared x. This is also known as the antiderivative of cosecx.
Prepare for integration by parts: