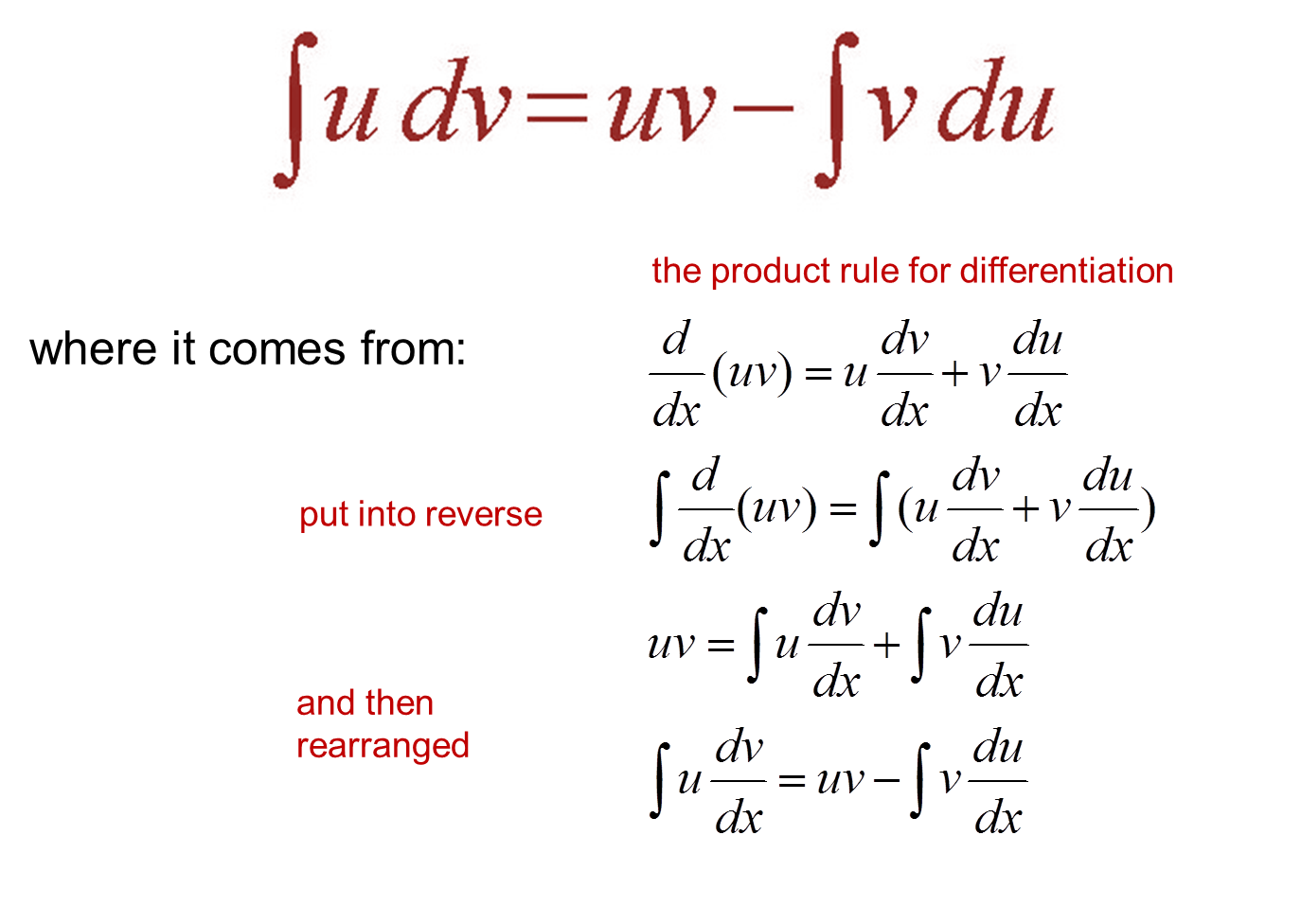If u and v are functions of x, then the bernoulli’s rule is. And v, v 1, v 2, v 3, are successive integrals of dv. When choosing uand dv, we want a uthat will become simpler (or at least no more complicated) when we
Integration By Parts Tutorial & Example Calculus 2
U is the function u(x) v is the function v(x) u' is the derivative of the function u(x)
Use derivative product rule (uv)0= d dx (uv) = du dx v + dv dx u = u0v + uv0;
We obtain a quotient rule integration by parts formula: You will see plenty of examples soon, but first let us see the rule: Integration can be used to find areas, volumes, central points and many useful things. Similar to this uv formula in differentiation, we have a uv formula for integration.
The first rule to know is that integrals and derivatives are opposites!.
Z udv= uv z vdu integration by parts (which i may abbreviate as ibp or ibp) \undoes the product rule. The integration formula of uv : Integral calculus formula sheet derivative rules: This method of integration is often used for integrating products of two functions.
∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx.
Bernoulli’s formula for integration by parts. U dv dx = d(uv) dx − v du dx. Some types of problems where you can use the method of integration by parts: Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways.
First solve it, according to this:
(2) as an application of the quotient rule integration by parts formula, consider the integral sin(x−1/2) x2 dx. The integration by parts formula states: Derivation of the formula for integration by parts we already know how to differentiate a product: Multiplication by constant ∫cf(x) dx = c∫f(x) dx
Let u = x1/2, dv = sin(x−1/2) x3/2 dx, du = 1 2 x−1/2 dx,v= 2cos(x−1/2).
Uv integration is one of the important methods to solve the integration problems. Sometimes we can work out an integral, because we know a matching derivative. D/dx (uv) = u (dv/dx) + v (du/dx) by integrating both the sides, we get; Integrate both sides and rearrange, to get the integration by parts formula
Are successive derivatives of u.
Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − integrals of rational and irrational functions 1 1 n x dx cn x n + = + ∫ + 1 dx x cln x ∫ = + ∫cdx cx c= + 2 2 x ∫xdx c= + 3 2 3 x ∫x dx c= + (1) (2) (3) (4) ˘ (5) ˇˆ˙ (6) (7) ˝˛ (8) ˚ˇ (9) ˚˜ integration by parts ∫udv=uv−∫vdu ˘ ˇ ˆ ˙ ˝ ˛ The first term on the right simplifies since we are simply integrating what has been differentiated. What is the formula of integration of uv?
∫u v dx = u∫v dx − ∫u’ (∫v dx) dx.
Uv = ∫u (dv/dx)dx + ∫v (du/dx)dx. Sum rule ∫(f + g) dx = ∫f dx + ∫g dx; In mathematics, integration by part basically uses the ilate rule that helps to select the first function and second function in the integration by parts method. For solving the above definite integral problem with integration by parts using rule 1, we have to apply limits after the end of our result.
Where u ′, u ′′, u ′′′,.
If u and v are any two differentiable functions of a single variable x. Bernoulli’s formula is advantageously applied when u = x n ( n is a positive integer) Dv u = v u + v u2 du. The product rule and integration by parts the product rule for derivatives leads to a technique of integration that breaks a complicated integral into simpler parts.
(uv)' = u'.v + u.v' also the two functions are often represented as f(x), and g(x), and the differentiation of the product of these two functions is d/dx (f(x).g(x)) = g(x).d/dx f(x) + f(x).
The rule can be thought of as an integral version of the product rule of differentiation. Let u and v are two functions then the formula of integration is. ∫ a b u ( x ) v ′ ( x ) d x = [ u ( x ) v ( x ) ] a b − ∫ a b u ′ ( x ) v ( x ) d x = u ( b ) v ( b ) − u ( a ) v ( a ) − ∫ a b u ′ ( x ) v ( x ) d x. Z u dv dx dx = z d(uv) dx dx − z v du dx dx.
The uv differentiation formula for two functions is as follows.
Integrating both sides and solving for one of the integrals leads to our integration by parts formula: Then, by the product rule of differentiation, we have; € ∫udv=uv−∫vdu hopefully this is a simpler integral to evaluate given integral that we cannot solve If y = uv then dy dx = d(uv) dx = u dv dx +v du dx.
Then sin(x−1/2) x2 dx = 2cos(x−1/2) x1/2 + 2cos(x−1/2) x · 1 2 x−1/2 dx = 2cos(x−1/2) x1/2 −2 cos(x−1/2)· −