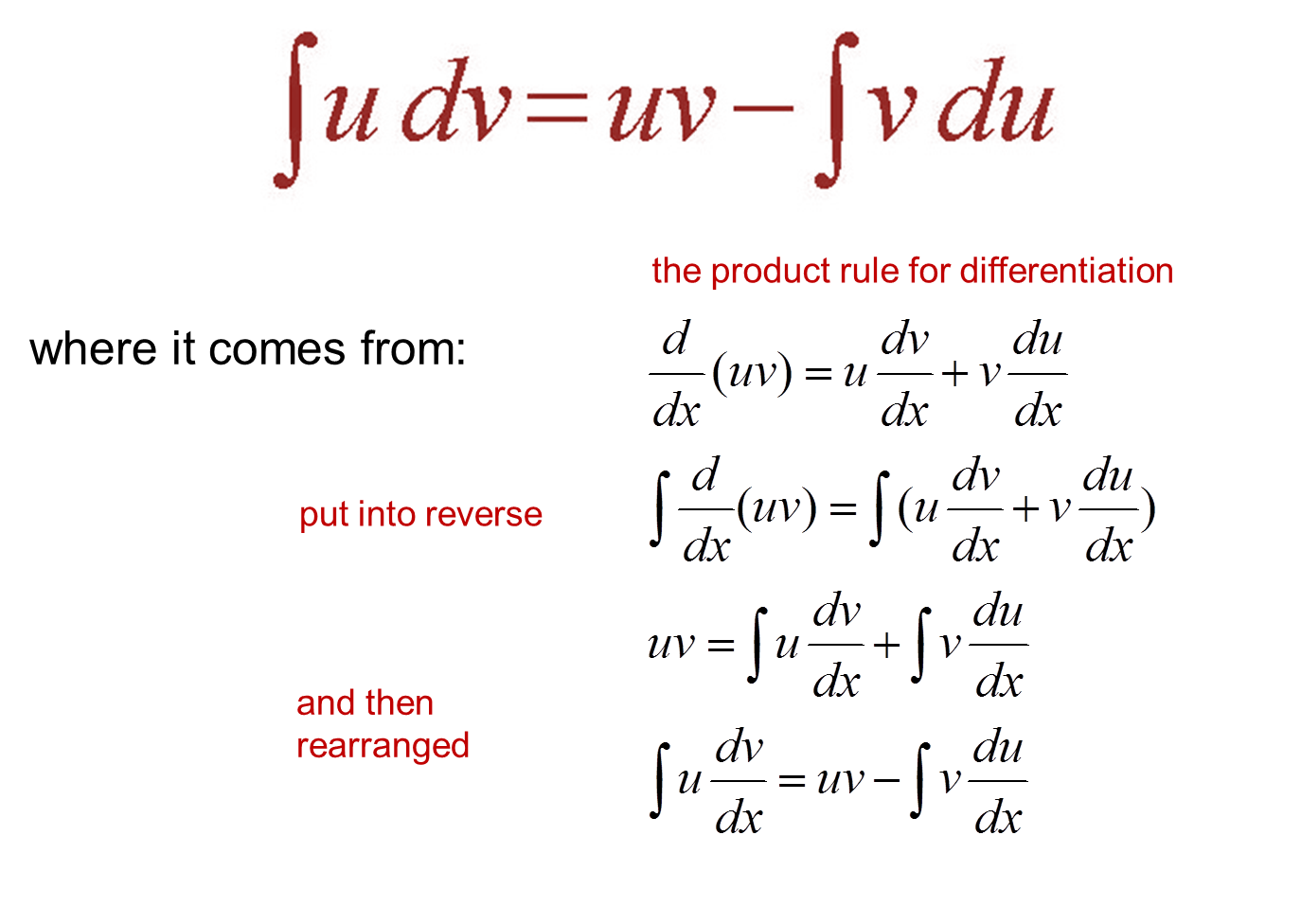Then we find a and b. For solving the above definite integral problem with integration by parts using rule 1, we have to apply limits after the end of our result. We solve this using a specific method.
Integration by parts Equation, Solved Example Problems
Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point.
!*+ ,˝˛ #$% &*+ , ˝˛ ' ( !
Z xcos(x2) dx = 1 2 z cos(x2)2x dx = 1 2 z cos(u) du = 1 2 (sin(u)) + c = sin(x2) 2 + c example 3. And v, v 1, v 2, v 3, are successive integrals of dv. Derivation of the formula for integration by parts we already know how to differentiate a product: Bernoulli’s formula for integration by parts.
This yields the formula for integration by parts :
Uv dx = uv − u v dx. Similar to this uv formula in differentiation, we have a uv formula for integration. Then du = 2x dx. Move to left side and solve for integral as follows:
They key is to remember that the second time around, you must use the “same type of substitution” as the first time.
Our equation becomes two seperate identities and then we solve. The uv differentiation formula for two functions is as follows. So we substitute 2x for u. As derived above, integration by parts uv formula is:
A s2 1 area of a triangle:
2 1 sin ( ) 1 cos(2 )x 2 sin tan cos x x x 1 sec cos x x cos( ) cos( ) x x 22sin ( ) cos ( ) 1xx 2 1 cos ( ) 1 cos(2 )x 2 cos cot sin x x x 1 csc sin x x sin( ) sin( ) x x 22tan ( ) 1 sec ( )x x geometry fomulas: Where we neglect writing the constant of integration. Z xcos(x2) dx set u = x2. Where u ′, u ′′, u ′′′,.
∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u.
(uv) = u v + uv uv = (uv) − u v uv dx = (uv) dx − u v dx uv dx = uv − u v dx the integration by parts formula is: Uv integration is one of the important methods to solve the integration problems. What is the formula of integration of uv? U = ln (x) v = 1/x 2.
Ln (x)' = 1 x.
Z cos(ln(x)) x dx set u = ln(x). Let u and v are two functions then the formula of integration is. See class notes for the details. Uvw uvw method is a useful technique for proving inequalities involving symmetric polynomials in three real nonnegative variables.
Odd powers of sec(x) or cosec(x) this uses a special integration by parts method.
These types of problems are common in contest mathematics. This method of integration is often used for integrating products of two functions. B b uv dx = uv| a b − u v dx. Px + q = a (d (√ (ax 2 + bx + c))/dx) + b.
U dv dx = d(uv) dx − v du dx.
(uv)' = u'.v + u.v' also the two functions are often represented as f(x), and g(x), and the differentiation of the product of these two functions is d/dx (f(x).g(x)) = g(x).d/dx f(x) + f(x). In this video tutorial you will learn about integration by parts formula of ncert 12 class in hindi and how to use this formula to find integration of functi. U = x 2 +7x+2 and u' = 2x+7. The basic idea is to introduce a specific change of variables that simplifies the original inequality.
−ln (x)/x − ∫ −.
Using the formula (uv)' = uv' + vu' = (x 5)sec 2 x+(tan x)(5x 4) = x 5 sec 2 x+5x 4 tan x = x 4 [xsec 2 x+tanx] example 2 : For definite integrals, it becomes: If y = uv then dy dx = d(uv) dx = u dv dx +v du dx. After each application of integration by parts, watch for the appearance of a constant multiple of the original integral.
∫u v dx = u∫v dx − ∫u’ (∫v dx) dx.
Bernoulli’s formula is advantageously applied when u = x n ( n is a positive integer) 1 2 ( cos(u)) + c = cos(2x) 2 + c we do the following integrals with less exposition: Then, at some point, you have to use integration by parts again. Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − integrals of rational and irrational functions 1 1 n x dx cn x n + = + ∫ + 1 dx x cln x ∫ = + ∫cdx cx c= + 2 2 x ∫xdx c= + 3 2 3 x ∫x dx c= +
The integration formula of uv :
Integration by parts uv formula. Integral of the form ∫ (px+q) √ ( ax 2 + bx + c ) dx. Z u dv dx dx = z d(uv) dx dx − z v du dx dx. 2∫ex cosx dx = ex cosx + ex sin x + c ∫ex x dx = (ex cosx + ex sin x) + c 2 1 cos answer note:
First solve it, according to this:
If u and v are functions of x, then the bernoulli’s rule is. Integration by parts, definite integrals. Note appearance of original integral on right side of equation. Are successive derivatives of u.