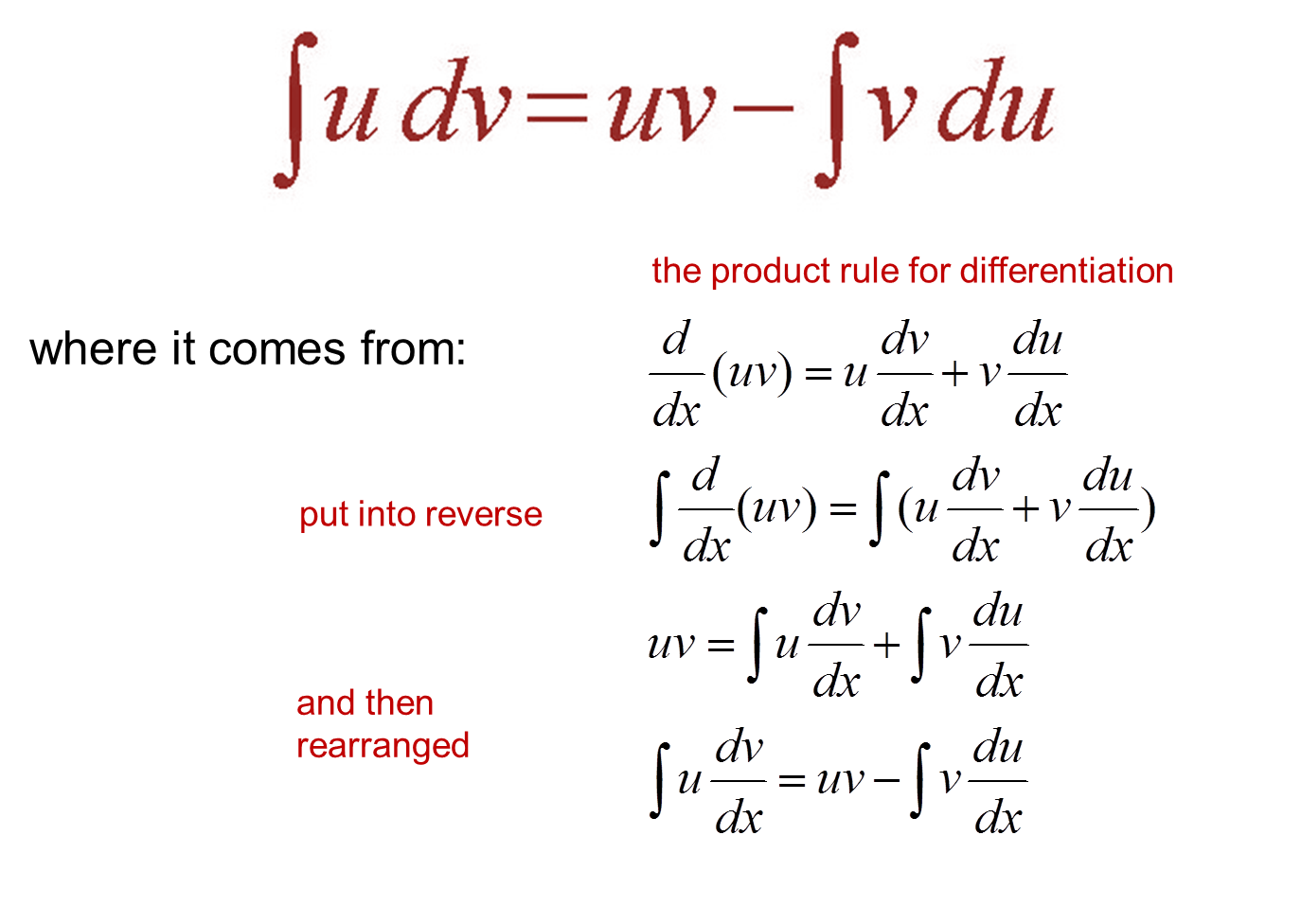Z u dv dx dx = uv − z v du dx dx. Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − integrals of rational and irrational functions 1 1 n x dx cn x n + = + ∫ + 1 dx x cln x ∫ = + ∫cdx cx c= + 2 2 x ∫xdx c= + 3 2 3 x ∫x dx c= + This is the formula known as integrationbyparts.
Fun Practice and Test Uv Integration Formula
Note as well that computing v v is very easy.
∫u v dx = u∫v dx − ∫u’ (∫v dx) dx
U = ln (x) v = 1/x 2. Click the blue arrow to submit. ∫sec 2 (ax + b)dx = (1/a)tan (ax + b) + c. While the other students thought this was a crazy idea, i was intrigued.
Typical use is with z f(x) g(x)dx, with g(x) = z g(x) dx known, so z f(x) g(x) dx = f(x)g(x) z g(x)f0(x)dx;
∫cos (ax + b)dx = (1/a)sin (ax + b) + c. Here is a list of commonly used integration formulas. Z u dv dx dx = z d(uv) dx dx − z v du dx dx. To use this formula, we will need to identify u u and dv d v, compute du d u and v v and then use the formula.
Below, i derive a quotient rule integration by parts formula, apply the resulting integration formula
Du u c 1 1 n udu cn u n ln du uc u edu e cuu 1 ln adu a cuu a sin cosudu u c cos sinudu u c sec tan2 udu u c csc cot2 uuc csc cot cscuudu uc sec tan secuudu uc 22 1 arctan du u c Uv integration is one of the important methods to solve the integration problems. $\int {{x^\gamma }dx = \frac{{{x^{\gamma + 1}}}}{r + 1} + c}$ 1a: One of the functions is called the ‘first function’ and the other, the ‘second function’.
∫ u dv = uv − ∫ v du.
Choose evaluate the integral from the topic. Since integration is almost the inverse operation of differentiation, recollection of formulas and processes for differentiation already tells the most important formulas for integration: Integrals of some special function s. G (x)dx, we obtain the familiar integration by parts formula udv= uv − vdu.
2 z ey cos(y) dy = ey sin(y)+ ey cos(y) z ey cos(y) = ey 2 sin(y)+cos(y).
Gfx f xdx gudu udv uv vdu integration rules: ∫(ex) = ex +c ∫ ( e x) = e x + c. This method of integration is often used for integrating products of two functions. De nite integral form is z b a u dv = (uv)
∫ (ax + b)ⁿdx = (1/a) (ax + b) (n + 1) / (n + 1) + c.
∫1/ (ax + b)dx = (1/a)log (ax + b) + c. Integrate both sides and rearrange, to get the integration by parts formula z u dv = uv z v du; Z cos ln(x) dx = The first term on the right simplifies since we are simply integrating what has been differentiated.
−ln (x)/x − ∫ −.
Integration formula when x is in the form ax + b. Now it’s time to plug those variables into the integration by parts formula: ∫(c) = x+c ∫ ( c) = x + c ( where c is a constant) ∫(cx) = cx2 2 +c ∫ ( c x) = c x 2 2 + c ( where c is a constant) ∫(xn) = xn+1 n+1 ∫ ( x n) = x n + 1 n + 1. D(uv) dx = u dv dx +v du dx.
(1) my student victor asked if we could do a similar thing with the quotient rule.
V = ∫ dv v = ∫ d v. One more integration by parts, u = ey, dv = sin(y) dy, ⇒ du = ey dy, v = −cos(y). ∫ x n d x = 1 n + 1 x n + 1 + c unless n = − 1 ∫ e x d x = e x + c ∫ 1 x d x = ln. Use derivative product rule (uv)0= d dx (uv) = du dx v + dv dx u = u0v + uv0;
$\int {kdx = kx + c} $ where $k$ is a constant.
U dv dx = d(uv) dx − v du dx. Integration by parts formula : ∫(logax) = 1 xlna +c ∫ ( l o g a x) = 1 x l n a + c. Substitution and integration by parts example evaluate i = z cos ln(x) dx.
Applications of each formula can be found on the following pages.
∫(1 x) = ln|x|+c ∫ ( 1 x) = l n | x | + c. ∫(ax) = ax loga +c ∫ ( a x) = a x l o g a + c. Z ey cos(y) dy = ey sin(y) − z ey sin(y) dy. The integral calculator solves an indefinite integral of a function.
All we need to do is integrate dv d v.
$\int {kf(x) = k\int {f(x)dx} }$ where $k$ is. Let u and v are two functions then the formula of integration is. ∫ udv = uv −∫ vdu ∫ u d v = u v − ∫ v d u. Next, work the right side of the equation out to simplify it.
Z ey cos(y) dy = ey sin(y) − h −ey cos(y)+ z ey cos(y) dy i.
Ln (x)' = 1 x. ∫e(a x + b) dx = (1/a)e(a x + b) + c.