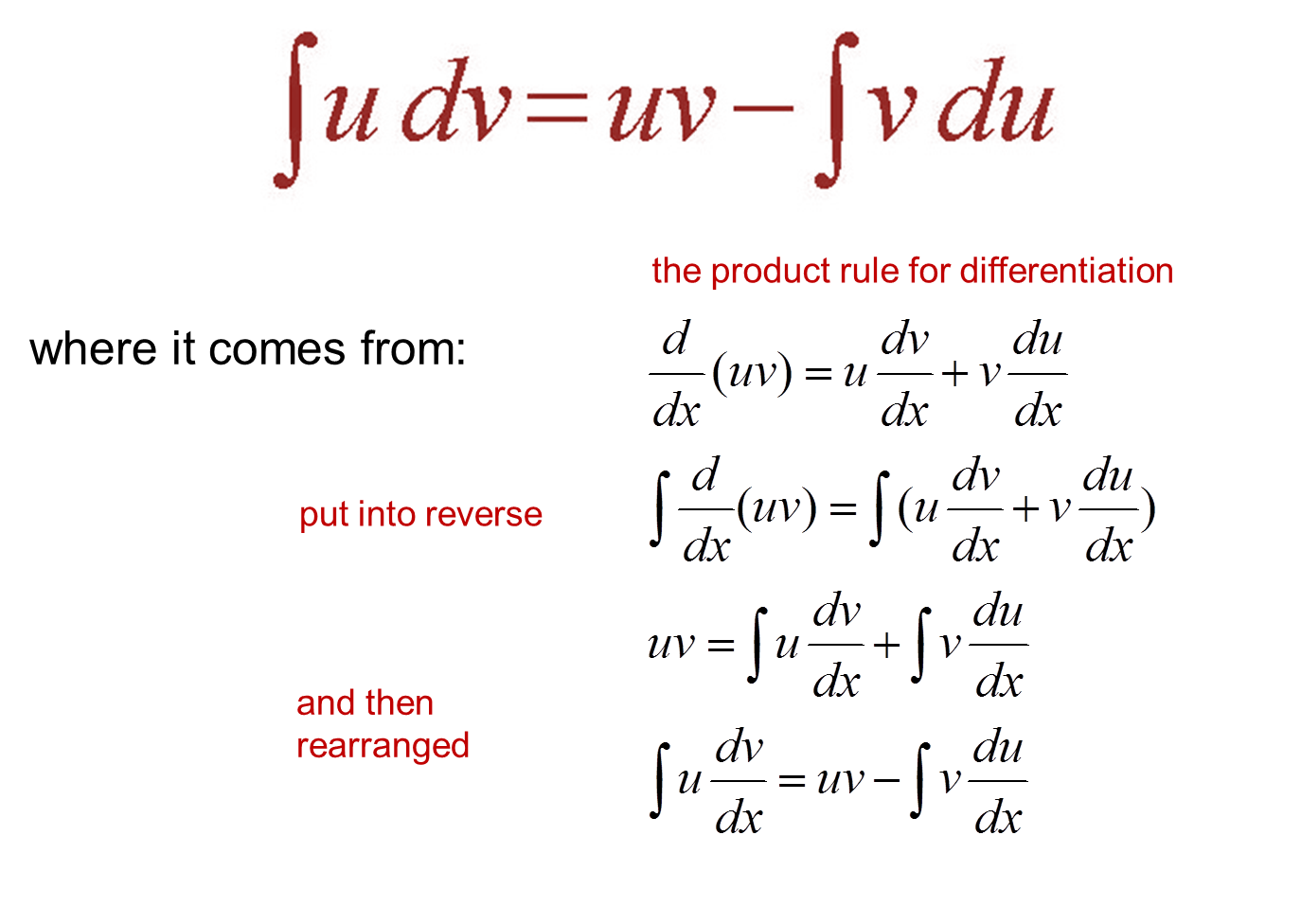Let u and v are two functions then the formula of integration is. U dv dx = d(uv) dx − v du dx. (5) ˇˆ˙ (6) (7) ˝˛.
Solved Now, The Integrationbyparts Formula Integral U D
Where we neglect writing the constant of integration.
The integration formula of uv :
To derive the formula for integration by parts we just rearrange and integrate the product formula: ∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u. The list of basic integral formulas are. Strategy for using integration by parts recall the integration by parts formula:
X sin (x) − ∫ sin (x) dx.
∫ cosx.dx = sinx + c; Since integration is almost the inverse operation of differentiation, recollection of formulas and processes for differentiation already tells the most important formulas for integration: ∫ x n d x = 1 n + 1 x n + 1 + c unless n = − 1 ∫ e x d x = e x + c ∫ 1 x d x = ln. ∫ sec 2 x dx = tan x + c.
Derivation of the formula for integration by parts we already know how to differentiate a product:
U' = x' = 1. This yields the formula for integration by parts : (1) (2) (3) (4) ˘. ∫ x n dx = ( (x n+1 )/ (n+1))+c ;
Use derivative product rule (uv)0= d dx (uv) = du dx v + dv dx u = u0v + uv0;
Integrate both sides and rearrange, to get the integration by parts formula If u and v are functions of x, then the bernoulli’s rule is. (uv) = u v + uv uv = (uv) − u v uv dx = (uv) dx − u v dx uv dx = uv − u v dx the integration by parts formula is: What are the integration formulas for trigonometric functions?
You just try to make numerator as a differential coefficient of denominator and then substitute as denominator =t and.
Integration by parts, definite integrals. Frequently, we choose u so that the derivative of u is simpler than u. And v, v 1, v 2, v 3, are successive integrals of dv. If y = uv then dy dx = d(uv) dx = u dv dx +v du dx.
∫a→b f (x) dx = ∫a→b f (t) dt.
(uv) = u v + uv combined with the fundamental theorem of calculus. ∫ 1 dx = x + c. Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − integrals of rational and irrational functions 1 1 n x dx cn x n + = + ∫ + 1 dx x cln x ∫ = + ∫cdx cx c= + 2 2 x ∫xdx c= + 3 2 3 x ∫x dx c= + What is the formula of integration of uv?
The trigonometric functions are simplified into integrable functions and then their integrals are evaluated.
∫ cos x dx = sin x + c. Z udv = uv − z v du. First choose which functions for u and v: ∫a→b f (x) dx = ∫a→c f (x) dx + ∫c→b f (x) dx.
A s2 1 area of a triangle:
Bernoulli’s formula for integration by parts. ∫ a dx = ax+ c. Z u dv dx dx = z d(uv) dx dx − z v du dx dx. ∫ sec 2 x.dx =.
Integration by parts and partial fractions integration by parts formula :
∫u v dx = u∫v dx − ∫u’ (∫v dx) dx. * see if u and v are both different functions in x then no such direct formula is there for integration of (u/v) dx. The first term on the right simplifies since we are simply integrating what has been differentiated. Some types of problems where you can use the method of integration by parts:
Are successive derivatives of u.
V = cos (x) so now it is in the format ∫u v dx we can proceed: The basic integration formulas for trigonometric functions are as follows. The integration by parts formula can also be written more compactly, with u substituted for f(x), v substituted for g(x), dv substituted for g’(x) and du substituted for f’(x): ∫ v dx = ∫ cos (x) dx = sin (x) (see integration rules) now we can put it together:
Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point.
To apply this formula we must choose dv so that we can integrate it! Bernoulli’s formula is advantageously applied when u = x n ( n is a positive integer) Uv integration is one of the important methods to solve the integration problems. This method of integration is often used for integrating products of two functions.