∫(1 x) = ln|x|+c ∫ ( 1 x) = l n | x | + c. X d x = − cos. ∫ sinx dx = −cosx+c 2.
Integration Formula For Trigonometry Function
By repeated use of the reduction formulas we can integrate any even power of tan x or cot x.
∫(c) = x+c ∫ ( c) = x + c ( where c is a constant) ∫(cx) = cx2 2 +c ∫ ( c x) = c x 2 2 + c ( where c is a constant) ∫(xn) = xn+1 n+1 ∫ ( x n) = x n + 1 n + 1.
X d x = sin. \(\int {\cos } \,x\,dx = \sin x + c\) However, only three integration formulas are noted in the rule on integration formulas resulting in inverse trigonometric functions because the remaining three are negative versions of the ones we use. ∫ cosx dx = sinx+c 1.
= 1 16 x 1 4 sin(4x).
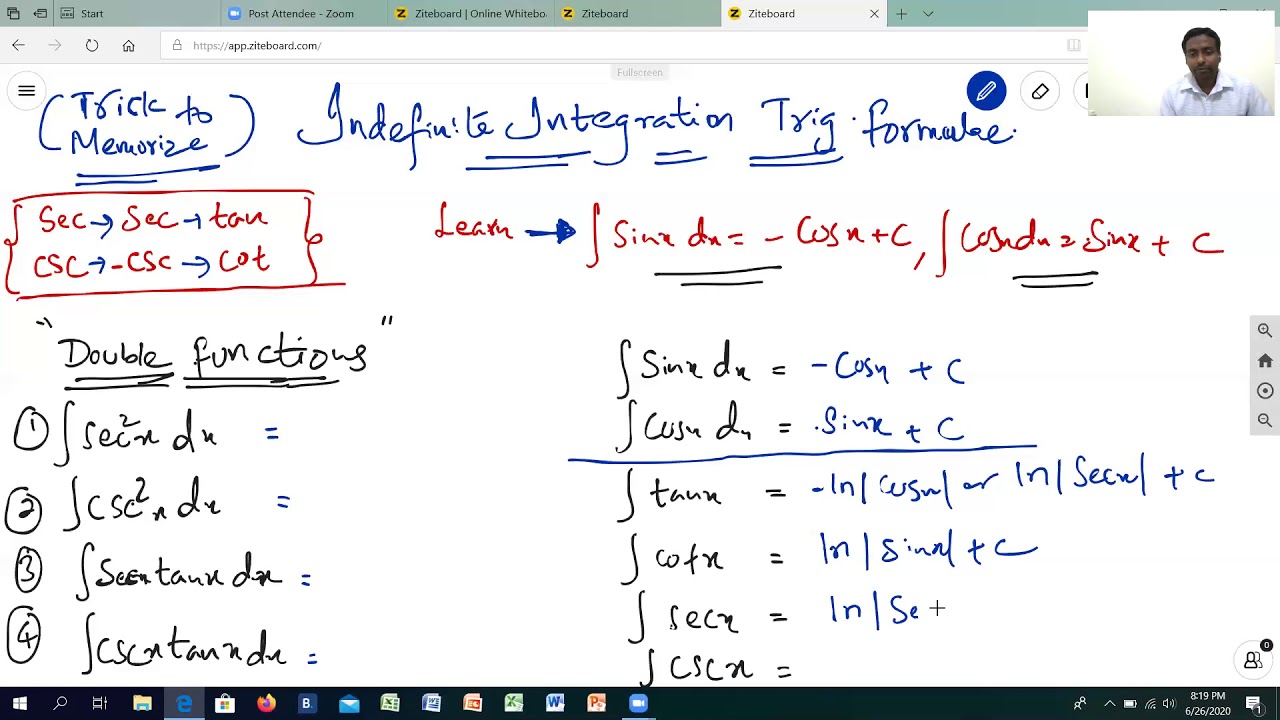
Integrals of trigonometric functions ∫sin cosxdx x c= − + ∫cos sinxdx x c= + ∫tan ln secxdx x c= + ∫sec ln tan secxdx x x c= + + sin sin cos2 1( ) 2 ∫ xdx x x x c= − + cos sin cos2 1 ( ) 2 ∫ xdx x x x c= + + ∫tan tan2 xdx x x c= − + ∫sec tan2 xdx x c= + integrals of exponential and logarithmic functions ∫ln lnxdx x x x c= − + ( ) 1 1 2 ln ln 1 1 n n x xdx x cn x x n n In chapter 2, we have discussed the derivatives of trigonometric funct. Cos((a b)x) a b +c the other integrals of products of sine and cosine follow similarly. The list of basic integral formulas are.
Fundamental integration formulas of trigonometric functions are as follows:
Let’s start off with an integral that we should already be able to do. ∫ cosxsin5xdx = ∫ u5du using the substitution u =sinx = 1 6 sin6x+c ∫ cos. 1 8 z sin2(2x)cos(2x) dx and now, we just integrate; Sin(ax)sin(bx)dx = 1 2 sin((a b)x) a b.
There are six inverse trigonometric functions.
∫(logax) = 1 xlna +c ∫ ( l o g a x) = 1 x l n a + c. A.) b.) e.) it is assumed that you are familiar with the following rules of differentiation. Some of the following trigonometry identities may be needed. Generally, if the function is any trigonometric function, and is its derivative, in all formulas the constant a is assumed to be nonzero, and c denotes the.
In this video, i discussed how to find the integration of two trigonometric functions.
1 2 sin((a+b)x)+sin((a b)x) dx = 1 2. The six basic formulas for integration involving trigonometric functions are stated in terms of appropriate pairs of. U) + c = − ln. We can also work the integral of any odd power of tan x or cot x down to an expression involving ∫ tan x or ∫ cot x.
∫ x n dx = ( (x n+1 )/ (n+1))+c ;
Calculus trigonometric derivatives and integrals strategy for evaluating r sinm(x)cosn(x)dx (a) if the power n of cosine is odd (n =2k +1), save one cosine factor and use cos2(x)=1sin2(x)to express the rest of the factors in terms of sine: For a complete list of antiderivative functions, see lists of integrals. ∫(ax) = ax loga +c ∫ ( a x) = a x l o g a + c. ∫ cos x dx = sin x + c.
∫ 1 dx = x + c.
1 r ∫ d x sin (x ± α) \frac{1}{r} \int \frac{dx}{\sin(x \pm \alpha)} r 1 ∫ sin (x ± α) d x and integrate it using the formula for ∫ csc (x) d x \displaystyle \int \csc(x)\, dx ∫ csc (x) d x. Sin3(2x) 48 + c 2. 4 integration involving secants and tangents. The only difference is whether the integrand is positive or negative.
1 8 1 6 sin3(2x) + c = x 16.
If a 6= b, then: X d x = sin. In this case, use a = r cos (α) a= r\cos(\alpha) a = r cos (α) and b = r sin (α) b= r\sin(\alpha) b = r sin (α) to put the integration in the form. The reduction formulas for the other trigonometric functions are obtained by using integration by parts.
Cos(ax)cos(bx)dx = 1 2 sin((a b)x) a b + sin((a+b)x) a+b +c.
The list of integral rules of trigonometric functions with proofs. In this section we are going to look at quite a few integrals involving trig functions and some of the techniques we can use to help us evaluate them. X d x = − cos. 1 8 z sin2(2x)cos(2x) dx = 1 16 z (1 cos(4x)) dx.
For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions.
∫ a dx = ax+ c. ∫(ex) = ex +c ∫ ( e x) = e x + c.