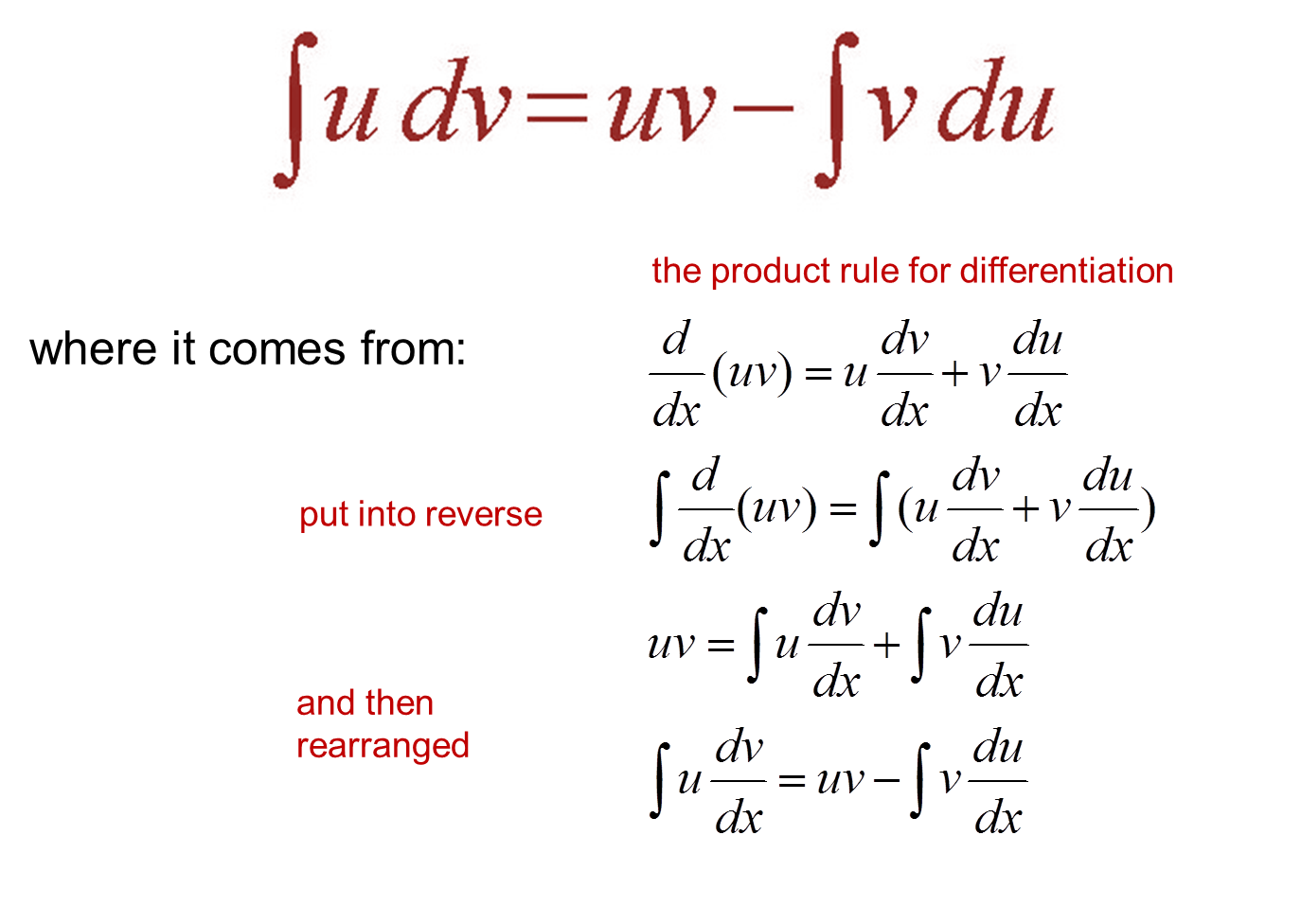Among the two functions, the first function f(x) is selected such that its derivative formula exists, and the second function g(x) is chosen such that an integral of such a function exists. You will see plenty of examples soon, but first let us see the rule: Now we integrate by parts!.
core pure 3 notes integration by parts examples
In order to evaluate the integrals, you must have a proper function.
A single integration by parts starts with.
Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways. Integration by parts is a technique for performing indefinite integration or definite integration by expanding the differential of a product of functions and expressing the original integral in terms of a known integral. Www.mathcentre.ac.uk 5 c mathcentre 2009 To do that, we let and :.
We can also sometimes use integration by parts when we want to integrate a function that cannot be split into the product of two things.
The integration by parts formula taught us that we use the by parts formula when we are given the product of two functions. \int x\cos\left (x\right)dx ∫ xcos(x)dx by applying integration by parts method to calculate the integral of the product of two functions, using the following formula. In order to compute the definite integral ∫ 1 e x ln. We can use the formula for integration by parts to find this integral if we note that we can write ln|x| as 1·ln|x|, a product.
U and dv are provided.
U = x, dv = cos x dx 3) ∫x ⋅ 2x dx; Let v = g (x) then dv = g‘ (x) dx. Where is a constant of integration. For example, if we have to find the integration of x sin x, then we need to use this formula.
Sometimes integration by parts must be repeated to obtain an answer.
Want to try more problems like. ∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx. In general, function , where is any real constant, leads to the correct differential ( x) d x, it is probably easiest to compute the antiderivative ∫ x ln.
U = ln x, dv = x dx evaluate each indefinite integral.
To reverse the product rule we also have a method, called integration by parts. Identify the two functions and work out which you want to integrate, and which to differentiate. ∫x2 sin x dx u =x2 (algebraic function) dv =sin x dx (trig function) du =2x dx v =∫sin x dx =−cosx ∫x2 sin x dx =uv−∫vdu =x2 (−cosx) − ∫−cosx 2x dx =−x2 cosx+2 ∫x cosx dx second application of integration by parts: Remember you can always check your work by differentiating your result!.
∫ x cos ( x) d x.
Using repeated applications of integration by parts: We choose dv dx = 1 and u = ln|x| so that v = z 1dx = x and du dx = 1 x. The ilate rule of integration considers the left term as the first function and the second term as the second function. By using this website, you agree to our cookie policy.
Then, z 1·ln|x|dx = xln|x|− z x· 1 x dx = xln|x|− z 1dx = xln|x|− x+c where c is a constant of integration.
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. Using u and v ', find u' and v. Previously, we found ∫ x ln. U is the function u(x) v is the function v(x) u' is the derivative of the function u(x)
If u and v are any two differentiable functions of a single variable x (say).
D d x ( u v) = u d v d x + v d u d x. We can solve the integral. The procedure does not always succeed, since some choices of may lead to. U = x, dv = ex dx 2) ∫xcos x dx;
The formula for integration by parts is then.
The formula is given by: ( x) d x = x ln. Here is a general method for integrating by parts: It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more.
Fill these values into the formula, and compute any further integrals.
We call this method ilate rule of integration or ilate rule formula. Let u = f (x) then du = f‘ (x) dx. For example, if the differential is , then the function leads to the correct differential. Using the integration by parts calculator is really easy and fast.
Let u = x then du = dx.
U = x, dv = 2x dx 4) ∫x ln x dx; ∫ u ⋅ d v = u ⋅ v − ∫ v ⋅ d u. Integration by parts formula is used for integrating the product of two functions. The trick we use in such circumstances is to multiply by 1 and take du/dx = 1.
X − 1 4 x 2 + c.
Integration by parts with a definite integral. This method is used to find the integrals by reducing them into standard forms. We can use the following notation to make the formula easier to remember. This can be rewritten as r f(u)du.
Integration by parts date_____ period____ evaluate each indefinite integral using integration by parts.
The two functions are generally represented as f(x) and g(x). Integration by parts of indefinite integrals let's find, for example, the indefinite integral. You need to enter your function in the function bar of the integration calculator. When working with the method of integration by parts, the differential of a function will be given first, and the function from which it came must be determined.
Integrating both sides, we get, u v = ∫ u d v d x d x + ∫.
5) ∫xe−x dx 6) ∫x2cos 3x dx 7. Then, by the product rule of differentiation, we have: