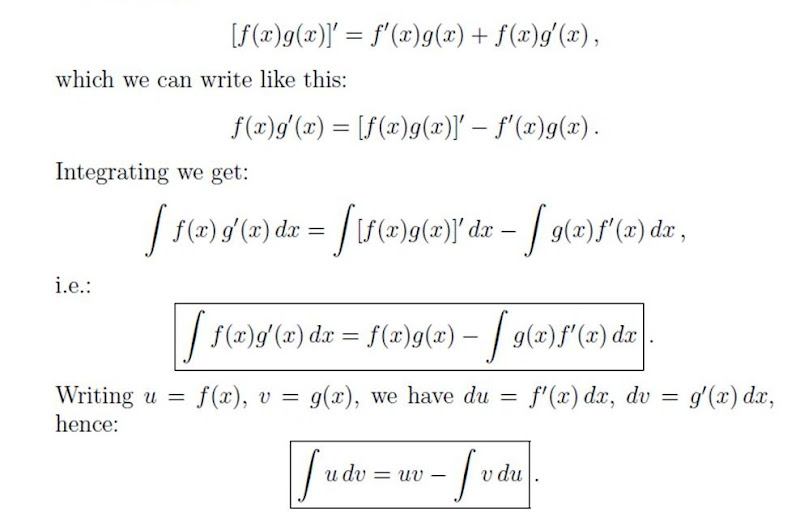Theorem for all differentiable functions g,f : = y 3 /3 + 0 (applying power and constant rule) = y 3 /3 + c. Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways.
Integration by parts
Integration by parts is used to integrate when you have a product (multiplication) of two functions.
In a way, it’s very similar to the product rule, which allowed you to find the derivative for two multiplied functions.
∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx. Now, integrate both sides of this. Integrating both sides, we get, u v = ∫ u d v. To reverse the product rule we also have a method, called integration by parts.
∫ u v dx = u ∫ v dx −∫ u ' (∫ v dx) dx.
(f g)′ =f ′g+f g′ ( f g) ′ = f ′ g + f g ′. It can be applied when two functions are in multiplication. Integration by parts formula, ∫u(x). You will see plenty of examples soon, but first let us see the rule:
You will see plenty of examples soon, but first let us see the rule:
Integration by part is a little complex rule. Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways. The integration by parts formula is an integral form of the product rule for derivatives: (ab)’ = ab’ + a’b
8.1) i integral form of the product rule.
In mathematics, integration by part basically uses the ilate rule that helps to select the first function and second function in the integration by parts method. $\int$ e cx.{sinsin cx or coscos cx}dx where c is constant. In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. What is integration by parts?
The second rule said that you can use the limit as you are going with integrals of functions to solve integration by parts definite integral with limits or bounds.
(fg)0 = f 0 g + f g0. By using this website, you agree to our cookie policy. I substitution and integration by parts. The formula is given by:
We’ll start with the product rule.
This method is called ilate rule. Integration by parts when the integral of function reappears. If u and v are any two differentiable functions of a single variable x (say). Integral form of the product rule remark:
With the product rule, you labeled one function “f”, the other “g”, and then.
Discover more science & math facts & information. → given the following integral, what derivative rule might we try to “reverse” to evaluate the integral 1 x x. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more. D d x ( u v) = u d v d x + v d u d x.
It is derived from the product rule of differentiation.
Then, by the product rule of differentiation, we have: Integration by parts essentially reverses the product rule for differentiation applied to (or ). In integration by parts, we have learned when the product of two functions are given to us then we apply the required formula. For example, you would use integration by parts for ∫x · ln(x) or ∫ xe 5x.
∫ (f g)′dx =∫ f ′g +f g′dx ∫ ( f g) ′ d x = ∫ f ′ g + f g ′ d x.
Let’s derive the equation for integration by parts. Integration by parts → the substitution rule for integrals allowed us to “reverse” the chain rule for derivatives and solve integrals such as 87 2 2 5 x x dx. The integral of the two functions are taken, by considering the left term as first function and second term as the second function. To do this integral we will need to use integration by parts so let’s derive the integration by parts formula.