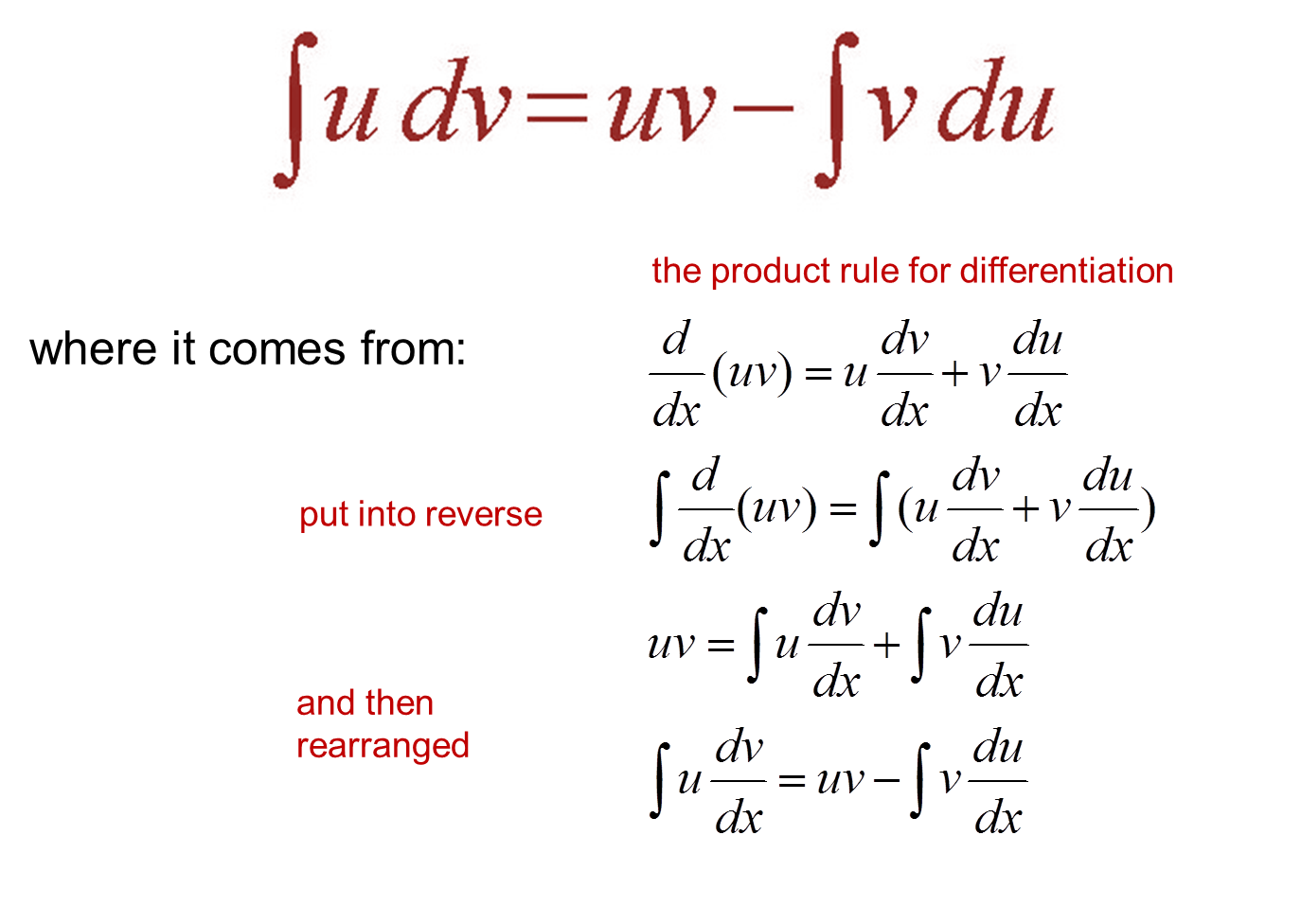The integration by parts formula is an integral form of the product rule for derivatives: (f g)′ =f ′g+f g′ ( f g) ′ = f ′ g + f g ′. (2) as an application of the quotient rule integration by parts formula, consider the integral sin(x−1/2) x2 dx.
Solved Use Integration By Parts To Establish A Reduction
To find the integration of the given expression we use the integration by parts formula:
To do this integral we will need to use integration by parts so let’s derive the integration by parts formula.
Integration by parts is a procedure used to integrate and it is quite beneficial when two functions are multiplied together, but is also helpful in other ways. We already found the value, du/dx = 1. For example, “x” is always a good choice because the. Then sin(x−1/2) x2 dx = 2cos(x−1/2) x1/2 + 2cos(x−1/2) x · 1 2 x−1/2 dx = 2cos(x−1/2) x1/2 −2 cos(x−1/2)· −
Ideally, your choice for the “u” function should be the one that’s easier to find the derivative for.
Every differentiation rule has a corresponding integration rule. To reverse the product rule we also have a method, called integration by parts. Here, let x is equal to u, so that after differentiation, du/dx = 1, the value we get is a constant value. We’ll start with the product rule.
D d x ( u v) = u d v d x + v d u d x.
∫ f ( x) g ′ ( x) d x = f ( x) g ( x) − ∫ g ( x) f ′ ( x) d x. D ( u v) d x × d x = u d v d x × d x + v d u d x × d x. Theorem for all differentiable functions g,f : ∫ u v d x = u d x − ∫ ( d u d x ∫ v d x) d x.
In mathematics, integration by part basically uses the ilate rule that helps to select the first function and second function in the integration by parts method.
D ( u v) = u d v + v d u. Integrating both sides, we get, u v = ∫ u d v d x. Integration by parts formula, ∫u(x). U is the function u(x) v is the function v(x) u' is the derivative of the function u(x)
The integration by parts formula is calculated as.
For solving the above definite integral problem with integration by parts using rule 1, we have to apply limits after the end of our result. Now, integrate both sides of this. First solve it, according to this: What is integration by parts formula.
D ( u v) × d x d x = u d v × d x d x + v d u × d x d x.
Let u = x1/2, dv = sin(x−1/2) x3/2 dx, du = 1 2 x−1/2 dx,v= 2cos(x−1/2). U is the function u(x) We obtain a quotient rule integration by parts formula: The integration by parts formula states:
There are two more methods that we can use to perform the integration apart from the integration by parts formula,.
The formula for integration by parts is: ∫ 𝑢𝑢𝑢𝑢𝑢𝑢 = 𝑢𝑢𝑢𝑢 − ∫ 𝑣𝑣𝑣𝑣𝑣𝑣. Now, since dv/dx = cos x ∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx.
The left part of the formula gives you the labels (u and dv).
Dv u = v u + v u2 du. Then, by the product rule of differentiation, we have: D ( u v) × 1 = u d v × 1 + v d u × 1. General steps to using the integration by parts formula:
There are plenty of examples, but first, it is important to clear the rule:
The formula for integration by parts becomes: If u and v are any two differentiable functions of a single variable x (say). Therefore, we have to apply the formula of integration by parts. ∫ a b u ( x ) v ′ ( x ) d x = [ u ( x ) v ( x ) ] a b − ∫ a b u ′ ( x ) v ( x ) d x = u ( b ) v ( b ) − u ( a ) v ( a ) − ∫ a b u ′ ( x ) v ( x ) d x.
The method of integration using partial fractions.
In mathematics, integration by part basically uses the ilate rule that helps to select the first function and second function in the integration by parts method. Integration by parts works when your integrand contains a function multiplied by the derivative of another function. D ( u v) d x × d x = ( u d v d x + v d u d x) × d x. I substitution and integration by parts.
∫u v dx = u∫v dx −∫u' (∫v dx) dx.
Multiply both sides of the equation by the differential element d x. We can also sometimes use integration by parts when we want to integrate a function that cannot be split into the product of two things. Choose which part of the formula is going to be u. (fg)0 = f 0 g + f g0.
The method of integration by substitution.
This is cumbersome, so we usually abbreviate by u =. You will see plenty of examples soon, but first let us see the rule: As per the formula, we have to consider, dv/dx as one function and u as another function. The formula is given by:
Again, u = x and dv/dx = cos x.
The rule that corresponds to the product rule for differentiation is called the rule for integration by parts (stewart, 2010). So the integration by parts formula can be written as: 8.1) i integral form of the product rule. Integral form of the product rule remark: