∫x2 sin x dx u =x2 (algebraic function) dv =sin x dx (trig function) du =2x dx v =∫sin x dx =−cosx ∫x2 sin x dx =uv−∫vdu =x2 (−cosx) − ∫−cosx 2x dx =−x2 cosx+2 ∫x cosx dx second application of integration by parts: (e) z sin(p x) dx. U = ln x, dv = x dx evaluate each indefinite integral.
Calculus Integration by Parts Practice Problem 1 YouTube
So g′(t) = 1 and f(t) = − 1 2 cos(2t).
R udv = uv r vdu (try to substitute uso that du dx is simpler than uand so that vis no more complicated than dv.) example.
U and dv are provided. Let u= cosx, dv= exdx. = =(=() + =() + + =() + + (() =′() = =) = = + = =() = (() + + (. Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point.
6.11 integration by parts calculus integrate the following.
We will show an informal proof here. The following are solutions to the integration by parts practice problems posted november 9. Sometimes integration by parts must be repeated to obtain an answer. 7 practice problems concerning integration by parts 1.
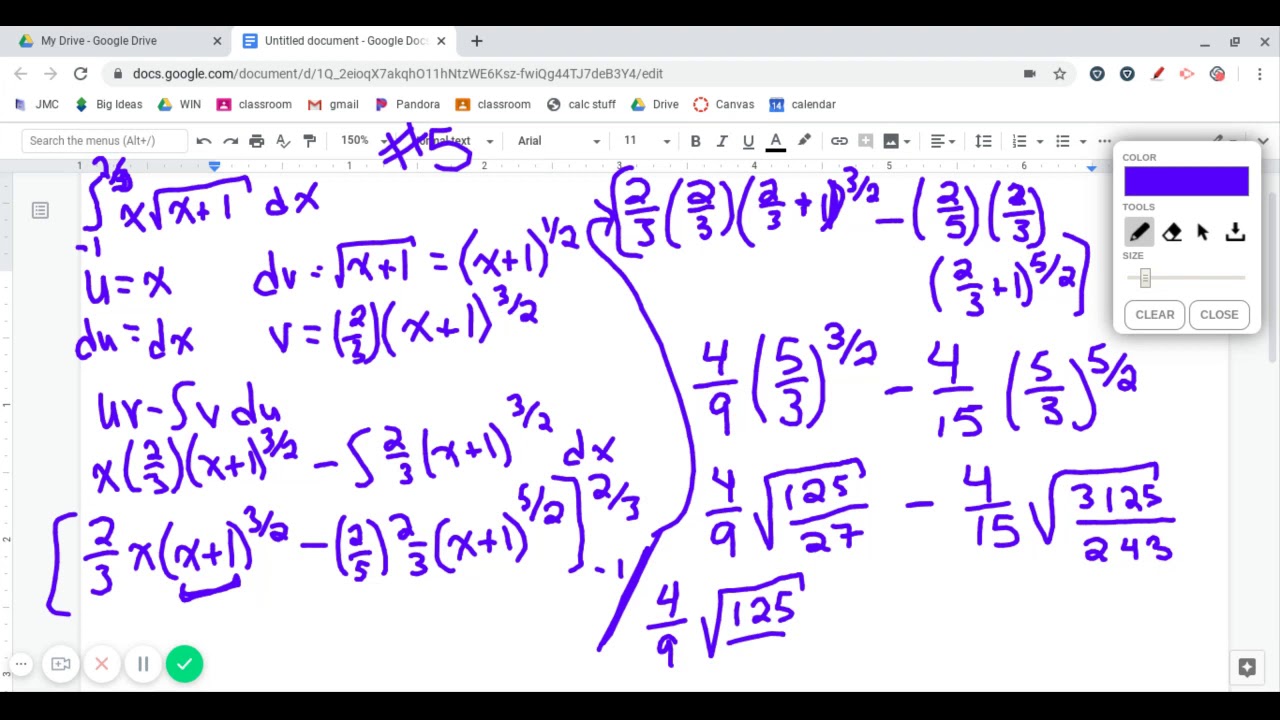
Ill 161 find the exact value of x2ex dr.
It is important to read the next section to understand where this comes from. ∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u. Practice evaluating definite integrals using integration by parts with practice problems and explanations. Inverse trig logarithm algebraic (polynomial) trig exponential 2.
(ii) hence use integration by parts to find the exact value of cosx sinx dr.
Let g(t) = t and f(t) = sin(2t). U = x, dv = 2x dx 4) ∫x ln x dx; Ì𝑥 6sin :𝑥 ;𝑑𝑥 4. Z tan 1(x) dx 3.
The integration by parts equation comes from the product rule for derivatives.
The solutions are not proven (c) z e 1 ln(x) dx. Then z exsinxdx= exsinx excosx z exsinxdx Integration by parts date_____ period____ evaluate each indefinite integral using integration by parts.
For some of you who want more practice, it™s a good pool of problems.
Evaluate inde nite integrals using integration by parts: Then du= cosxdxand v= ex. [5] (i) use integration by parts to find x sec2x dr. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
If you're seeing this message, it means we're having trouble loading external resources on our website.
Math ap®︎/college calculus bc integration and accumulation of change using integration by parts. I pick the representive ones out. Many exam problems come with a special twist. \displaystyle dv=e^ {x}dx dv = exdx.
5) ∫xe−x dx 6) ∫x2cos 3x dx 7) ∫ x2 e2x
[4] [3] evaluate x cosx dx, giving your answer in an exact form [5] Review your integration by parts skills. Practice problems on integration by parts (with solutions) this problem set is generated by di. \displaystyle \int (4x+7)e^ {x}dx ∫ (4x+7)exdx using integration by parts.
R u dv = uv r v du.
Z x2 sin(x) dx 6. (ii) hence find xtan2x dr. Z ln(x) x2 dx 5. V= cosxdx xcosx+ z cosxdx = xcosx+sinx notice that in the above, setting u= xyields du dx = 1 (i.e., du= dx), which is simpler
Integration by parts, definite integrals.
Z xex ln(x 1) dx 3. 1)view solution 2)view solution 3)view solution 4)view solutionpart (a): Then z exsinxdx= exsinx z excosxdx now we need to use integration by parts on the second integral. [6] find the exact value of x inxdx.
Generally, picking u in this descending order works, and dv is what’s left:
What is the integration by parts formula? Z x4 tan 1(x) dx 5. Z ex cos(x) dx 5 challenge problems concerning integration by parts 1. ( 2 − 3 x) d x solution.
Integration by parts (practice) | khan academy.
Let u= sinx, dv= exdx. Dv= sinxdx = du= dx; When working with the method of integration by parts, the differential of a function will be given first, and the function from which it came must be determined. ∫ ( 4 x + 7) e x d x = ( 4 x − 3) e x + c.
An assortment of integrals from midsemester topics:
Then du= sinxdxand v= ex. (d) z ex cos(x) dx. Z sin 1(x) dx 2. Using repeated applications of integration by parts:
Then, ˆ tsin(2t)dt = − 1 2 tt)+ 1)) +)+ =))+ (x) = x().
Integration by parts, trig and trig substitution integrals, partial fractions decomposition/integrals ∫ 0 6 (2 +5x)e1 3xdx ∫ 6 0 ( 2 + 5 x) e 1 3 x d x solution. U = 4 x + 7, \displaystyle u=4x+7, u = 4x+7, d v = e x d x. Integration by parts practice questions courtesy:
U = x, dv = cos x dx 3) ∫x ⋅ 2x dx;
We have z xsinxdx u= x; ∫ ( 4 x + 7) e x d x. U = x, dv = ex dx 2) ∫xcos x dx; In general, function , where is any real constant, leads to the correct differential
For example, if the differential is , then the function leads to the correct differential.
Then, (())))) + +) =) +) + =) + (((′() = =. Let u and v be functions of t.