Between x 2 and e x the factor e x is more sophisticated and you can integrate it, so let d v = e x d x and then u = x 2. Our application and enrollment process does not follow a first come,first served process. I'm sorry, but you did ask:
Fun Practice and Test Uv Integration Formula
You also asked about integrating x ln.
Integration by parts, definite integrals.
Conversely, leaving the order alone might result in integrals that are difficult or impossible to integrate. The liate method was rst mentioned by herbert e. ∫x2 sin x dx u =x2 (algebraic function) dv =sin x dx (trig function) du =2x dx v =∫sin x dx =−cosx ∫x2 sin x dx =uv−∫vdu =x2 (−cosx) − ∫−cosx 2x dx =−x2 cosx+2 ∫x cosx dx second application. This is cumbersome, so we usually abbreviate by u = f ( x), v = g ( x) so that d u = f ′ ( x) d x and d v = g ′ ( x) d x.
In mathematics, integration by part basically uses the ilate rule that helps to select the first function and second function in the integration by parts method.
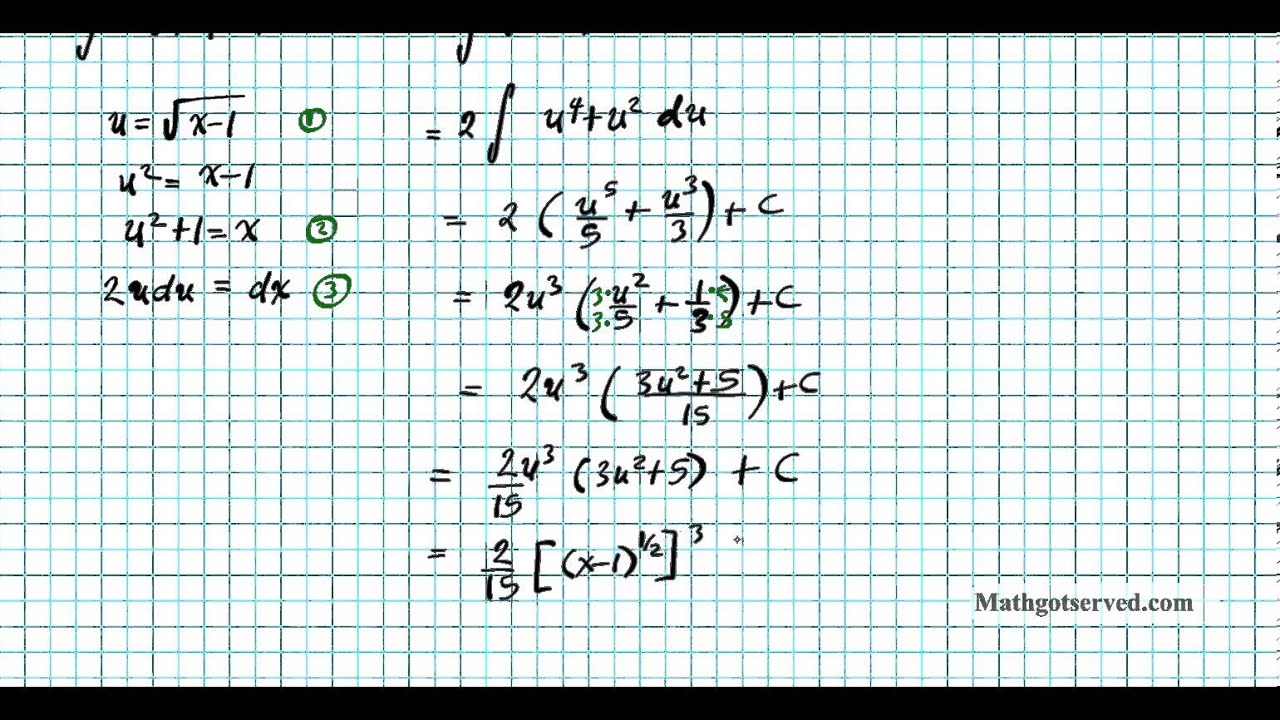
∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u. ∫ u d v = u v − ∫ v d u. (c) the function which can be integrated easily should be. First choose which functions for u and v:
U' = x' = 1.
It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more. Usually, the preference order of this rule is based on some functions such as inverse, algebraic, logarithm, trigonometric, exponent. The integration of uv formula is a special rule of integration by parts. Integration by parts is the “unproduct rule.” the formula for integration by parts is integration by parts:
31st national conference of christian.
And the answer to that question is to follow the formula for integration by parts. Order of operations factors & primes fractions long arithmetic decimals exponents & radicals ratios & proportions percent modulo mean, median & mode scientific notation arithmetics. As mentioned above, integration by parts uv formula is: ∫ u d v = u v − ∫ v d u.
In general, you want $u$ to be easier to differentiate, whereas $dv$ to be easier to integrate.
Changing the order of integration sometimes leads to integrals that are more easily evaluated; In your example, however, if you follow the rule above, both functions should be $u$. You must learn this formula. This is cumbersome, so we usually abbreviate by u = f ( x), v = g ( x) so that d u = f ′ ( x) d x and d v = g ′ ( x) d x.
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative.
Listed in order of preference. The applications are collected then sorted by preference order. Using repeated applications of integration by parts: Tabular integration by parts when integration by parts is needed more than once you are actually doing integration by parts.
Suppose, we have to integrate x ex, then we consider x as first function and ex as the second function.
Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point. The preference order of this rule will be dependent on some functions like inverse, algebraic, logarithm, trigonometric, exponent, according to the ilate rule. Changing the order of integration. V = cos(x) so now it is in the format ∫ u v dx we can proceed:
∫ f ( x) g ′ ( x) d x = f ( x) g ( x) − ∫ g ( x) f ′ ( x) d x.
You can check wikipedia's page on integration by parts, and in particular the liate rule. What is integration of u v? Indicate your choice of workshop among the above list by preference order (1, 2 or 3). Examples of order of preference in a sentence, how to use it.
∫ v dx = ∫ cos(x) dx = sin(x) (see integration rules) now we can put it together:
How do i end up with the following via integration by parts? (b) the function which can’t be integrated easily should be assumed to be the second function. ∫ f ( x) g ′ ( x) d x = f ( x) g ( x) − ∫ g ( x) f ′ ( x) d x. Integration by parts of uv formula.
Du and v are consequences of these two choices.
Order of integration refers to changing the order you evaluate iterated integrals—for example double integrals or triple integrals. Sometimes integration by parts must be repeated to obtain an answer. 2 \liate and tabular intergration by parts and so z x3ex2dx = x2 1 2 ex2 z 1 2 ex22xdx = 1 2 x2ex2 z xex2dx = 1 2 x2ex2 1 2 ex2 + c = 1 2 ex2(x2 1) + c: Ok, we have x multiplied by cos(x), so integration by parts is a good choice.
You must learn this formula.
Choose as d v the most complicated expression in the integrand that you currently know how to integrate. While integrating by parts, (a) any function can be assumed to be the first or the second. Hence i = ex / x + c. ∫udv uv vdu=−∫ when using the integration by parts method you must choose u and dv;