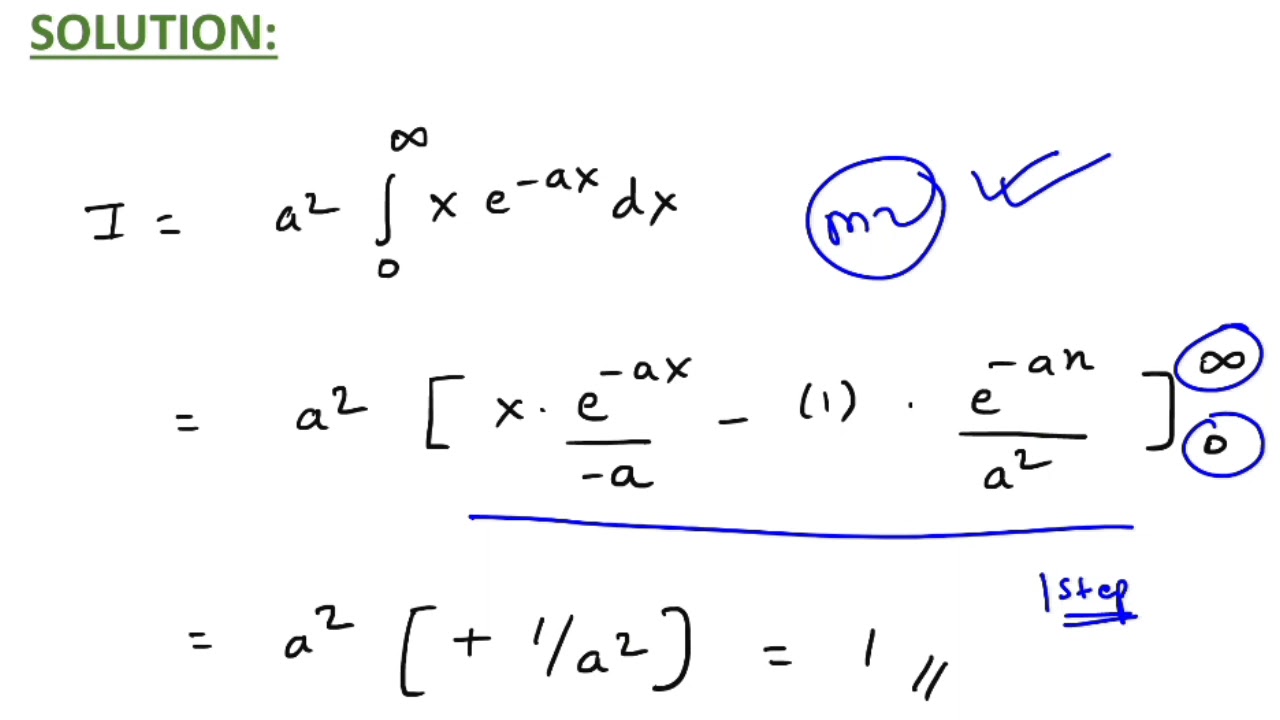∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx. U dv dx = d(uv) dx − v du dx. Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways.
Pdf of integration by part
Learn more about the proof, applications of integration by parts formula.
Uv = (uv) − u v uv dx = (uv) dx − u v dx uv dx = uv − u v dx the integration by parts formula is:
The integration by parts formula may be stated as: Again, u = x and dv/dx = cos x. Integration by parts, definite integrals. To derive the formula for integration by parts we just rearrange and integrate the product formula:
∫ u dv = uv − ∫ v du.
Use derivative product rule (uv)0= d dx (uv) = du dx v + dv dx u = u0v + uv0; You will see plenty of examples soon, but first let us see the rule: Sometimes integration by parts must be repeated to obtain an answer. While the other students thought this was a crazy idea, i was intrigued.
U is the function u(x) v is the function v(x) u' is the derivative of the function u(x)
But what if we are required to figure out the integral of a product of two functions? Some types of problems where you can use the method of integration by parts: Now, since dv/dx = cos x This means that step 2 now, since u=4x, then du=4 dx.
U = function of u(x) v = function of v(x) dv = derivative of v(x) du = derivative of u(x) read more:
Combined with the fundamental theorem of calculus. Apply the integration by parts formula: (5) ˇˆ˙ (6) (7) ˝˛. The first term on the right simplifies since we are simply integrating what has been differentiated.
This means that dv dt step 2 now, since u=arctan(9t), then du dt 1 +8112 1+81t2
Integration by parts is the technique used to find the integral of the product of two types of functions. Therefore, we have to apply the formula of integration by parts. Uv dx = uv − u v dx. As per the formula, we have to consider, dv/dx as one function and u as another function.
Integration by parts and partial fractions integration by parts formula :
Integration by parts is the answer to this. G (x)dx, we obtain the familiar integration by parts formula udv= uv − vdu. Derivation of the formula for integration by parts we already know how to differentiate a product: Since the goal is to produce a simpler integral, we will choose u = 4x.
³ 2 sinx dx u x2 (algebraic function) dv sin x dx (trig function) du 2x dx v ³sin dx cosx ³ 2 sinx dx uv ³vdu 2 ( ) ³ cos 2x dx 2 2 ³cosx dx second application of integration by parts:
U =sin−1 x (inverse trig function) dv =1 dx (algebraic function) dx Integration by parts uv formula. (1) my student victor asked if we could do a similar thing with the quotient rule. (1) (2) (3) (4) ˘.
∫uv dx = u∫v dx − ∫((du/dx)∫v dx) dx
Integrate both sides and rearrange, to get the integration by parts formula z u dv = uv z v du; (uv) = u v + uv. In calculus, for every kind of function, there exists a formula to directly evaluate their integral. ∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u.
∫sin−1 x dx *at first it appears that integration by parts does not apply, but let:
The formula for integration by parts is given as: Here, let x is equal to u, so that after differentiation, du/dx = 1, the value we get is a constant value. This yields the formula for integration by parts: U x (algebraic function) (making “same” choices for u and dv) dv cosx.
As mentioned above, integration by parts uv formula is:
(uv) = u v + uv. Below, i derive a quotient rule integration by parts formula, apply the resulting integration formula ∫sin x ln(cosx) dx = uv − ∫vdu =(ln(cosx))(−cosx) −∫(−cosx)(−tan x)dx =− −∫ dx x x x x x cos sin cos ln(cos ) (cos ) =−cosx ln(cosx) −∫sin x dx =−cosx ln(cosx) + cosx + c answer example c: Typical use is with z f(x) g(x)dx, with g(x) = z g(x) dx known, so z f(x) g(x) dx = f(x)g(x) z g(x)f0(x)dx;
Integration by parts is like the reverse of the product formula:
If y = uv then dy dx = d(uv) dx = u dv dx +v du dx. What i often do is to derive it from the product rule (for differentiation), but this isn't very efficient. Next, work the right side of the equation out to simplify it. We already found the value, du/dx = 1.