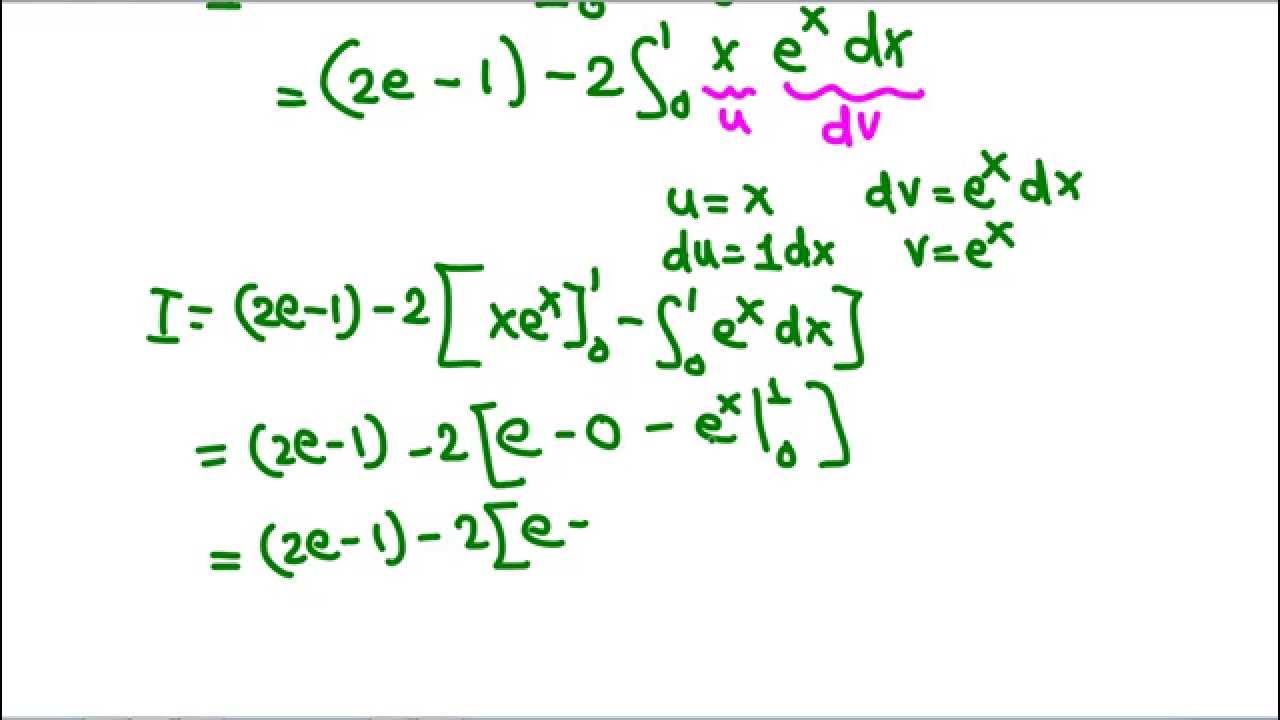Khan academy is a 501(c)(3) nonprofit organization. This one a bit deeper: X − 1 4 x 2 + c.
Integration Formulas Trig, Definite Integrals Class 12
\(\int_b^af\left(x\right)dx \), where b is the lower limit and a is the upper limit of the integral
The definite integration by parts formula is given as :
∫ b a f ( x) g ( x) d x = f ( x) ∫ b a g ( x) d x − ∫ b a [ d f ( x) d x ∫ b a g ( x) d x] d x. As per the formula, we have to consider, dv/dx as one function and u as another function. Same deal with this short form notation for integration by parts. The integration technique is really the same, only we add a step to evaluate the integral at the upper and lower limits of integration.
V' = 2 xe x 2.
Definite integration by parts formula is generally used to integrate the product of two functions. It's easier to see how to take the parts. Integration by parts for definite integrals. Here, let x is equal to u, so that after differentiation, du/dx = 1, the value we get is a constant value.
For example, the indefinite integral ∫ x cos x d x can be found with the help of integration by parts to be.
We need to use the factor trick on this one. We can integrate by parts on a definite integral, remembering to evaluate limits on each term. Integration by parts is the inverse of the product rule for derivatives. ∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u.
Integration by parts, definite integrals.
In the above definite integration by parts formula. ( x) d x without the limits of itegration (as we computed previously), and then use ftc ii to evalute the definite integral. If we rewrite the integrand as. ( x sin x) | a b = b sin b − a sin a.
First solve it, according to this:
Are the two formulas equivalent or not? (a) use integration by parts to show that b a f(x) dx = bf(b) − af(a) − b a xf (x) dx (b) use the result in part (a) to show that if y = f(x), then b a f(x) dx = bf(b) − af(a) − f(b) f(a) f − 1 (y) dy (c) show that if. The purpose of this problem is to show that if this condition is satisfied and if f is continuous, then a definite integral of f − 1 can be expressed in terms of a definite integral of f. Explanation of definite integration by parts formula is as follows:
Can we write the integration by parts for definite integral the following way:
D/dx [f (x)·g (x)] = f' (x)·g (x) + f (x)·g' (x) becomes. We already found the value, du/dx = 1. In calculus, the integration by parts is a special rule for integrating the product of two functions. Definite integration by parts formula is generally used to integrate the product of two functions.
P represents the function p(x)
(1 week ago) math ap®︎/college calculus bc integration and accumulation of change using integration by parts. Definite integration by parts formula. The definite integral has a unique value and is denoted by; Now that we have used integration by parts successfully to evaluate indefinite integrals, we turn our attention to definite integrals.
The following example illustrates its.
Again, u = x and dv/dx = cos x. To calculate the integration by parts, take f as the first function and g as the second function, then this formula may be pronounced as: The definite integration by parts formula is given as : (fg)' = f'g + fg'.
Evaluate the definite integral using integration by parts with way 2.
∫udv = uv − ∫vdu. Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point. ∫ x cos x d x = x sin x − ∫ sin x d x. My book gives the following formula for definite integral integration by parts:
Therefore, we have to apply the formula of integration by parts.
With a definite integral, that becomes. P is the function p (x), q is the function q (x), and. For solving the above definite integral problem with integration by parts using rule 1, we have to apply limits after the end of our result. Thanks to all of you who support me on patreon.
∫ a b x cos x d x = ( x sin x) | a b − ∫ a b sin x d x.
∫ b a f ( x) g ( x) d x = [ f ( x) ∫ g ( x) d x] b a − ∫ b a [ d f ( x) d x ∫ g ( x) d x] d x. Integration by parts with a definite integral. This article talks about the development of integration by parts: The formula used for this special type of integration rule is given below: