Integration By Parts Formula Fg PPT 6.1 PowerPoint Presentation

Let t > 1 and let f = χ [ 0, 1] be the characteristic function of [ 0, 1]. Theorem for all diﬀerentiable functions g,f : (fg)0= f0g+ fg0, and the barrow rule:

Integration by parts

∫ f ( x ) g ( x ) d x {\displaystyle \int f(x)g(x)\mathrm {d} x} integrals that would otherwise be difficult to solve can be put.

Prove the integration by parts formula:

Practice problem 1 z xcos(5x) dx let: We already found the value, du/dx = 1. Again, u = x and dv/dx = cos x. R → r holds z f (x) g0(x) dx = f (x) g(x) − z f 0(x) g(x) dx.

Fg= z fg 0dx+ z fgdx z fg0dx= fg z f0gdx or with uvas variables:

The integration by parts formula can also be written more compactly, with u substituted for f(x), v substituted for g(x), dv substituted for g’(x). Knowing which function to call u and which to call dv takes some practice. What is curious is that the. For two differentiable functions, f and g, fg = z fg0 + z f0g.

Show activity on this post.

Also closed under multiplication, i.e., fg 2aif f, g 2a. We’ll start with the product rule. See, for example, [12] and references therein. It remains to show that a= c2[a,b].

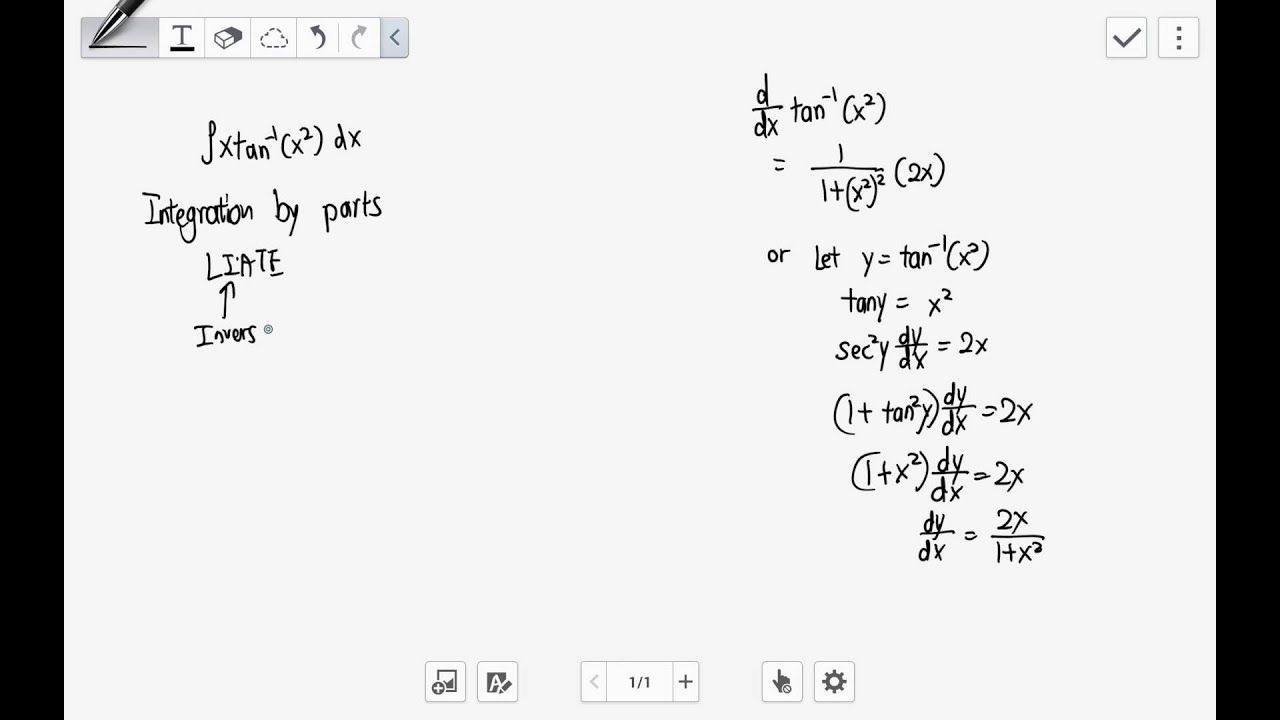
U inverse trig function (sin ,arccos , 1 xxetc) logarithmic functions (log3 ,ln( 1),xx etc) algebraic functions (xx x3,5,1/, etc)

Integration by parts product formula: U is the function u(x) v is the function v(x) u' is the derivative of the function u(x) Integrate the product rule f g0 = (fg)0 − f 0 g, and use the fundamental theorem of calculus in z (fg)0 dx = fg. Gration by parts formula, we point out that the formula holds if either f′ or g′ is continuous.

Math 242 integration by parts february 2009 you must know the following integration by parts formula:

The product rule for differentiation says. D dx (fg) = fg0+ f0g integrate on both sides: We’ll start with the product rule. ∫ a b f ′ ( x) g ( x) d x = ( f ( b) g ( b) − f ( a) g ( a)) − ∫ a b f ( x) g ′ ( x) d x.

Show activity on this post.

When trying to use this formula on real integrals, there are a number of shortcuts and/or organized techniques that. So integration by parts, i'll do it right over here, if i have the integral and i'll just write this as an indefinite integral but here we wanna take the indefinite integral and then evaluate it at pi and evaluate it at zero, so if i have f of x times g prime of x, dx, this is going to be equal to, and in other videos we prove this, it really just comes. F(x) = x g0(x) = cos(5x) dx f0(x) = dx g(x) = sin(5x) 5 z fg0dx= fg z f0gdx 1 So let's just remind ourselves about integration by parts.

Fg = ò(f 'g)(x)dx = òf '(x)g(x)dx + òf(x)g'(x)dx.

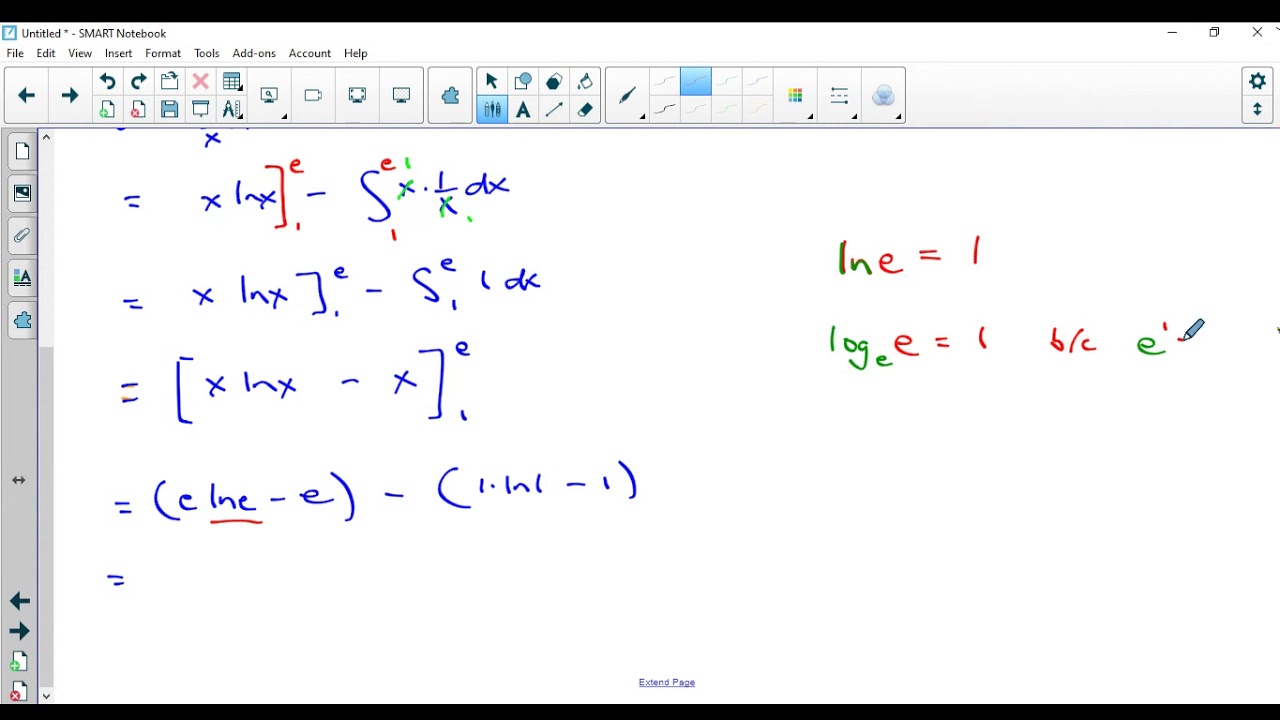
Therefore, we have to apply the formula of integration by parts. To do this integral we will need to use integration by parts so let’s derive the integration by parts formula. ∫ − t t f g ′ = ∫ 0 1 g ′ = g ( 1) − g ( 0). [ a, b] → r be differentiable such that f ′.

[a;b] !r which admit derivative.

Fg b a = z b a (fg)0dt= z b a (f0g+ fg0)dt: Now, since dv/dx = cos x I’ve written the formula as above because it’s very easy to remember in this form.) To do this integral we will need to use integration by parts so let’s derive the integration by parts formula.

Integrate the product rule f g0 = (fg)0 −f0 g, and use the fundamental theorem of calculus in z (fg)0 dx = fg.

Here, let x is equal to u, so that after differentiation, du/dx = 1, the value we get is a constant value. (fg)0 = f 0 g + f g0. On the other hand, since f ′ = 0 a.e., ∫ − t t f ′ g = 0. The classic integration by parts formula is z udv= uv z vdu which comes from integrating the product rule (fg)0= f0g+ fg0.

The usual rule of integration by parts taught in high school say that z b a fg0dt= fg b a z b a gf0dt;

Here is a general guide: Find the derivatives for the two parts in step 1: The integration by parts formula is an integral form of the product rule for derivatives: This yields the formula for integration by parts:

Insert your solutions from step 1 and 2 into the formula:

You will see plenty of examples soon, but first let us see the rule: Integration by parts msc 2000: The integration by parts formula is an integral form of the product rule for derivatives: (fg)0 = f0 g +f g0.

Prove the integration by parts formula:

[ a, b] → r are continuous. (fg f g fg)′= +′′ now, integrate both sides of this. If we integrate this relationship we obtain. As per the formula, we have to consider, dv/dx as one function and u as another function.

Fg means f(x)g(x) and r f means r f(x)dx.

(fg)' = f 'g + fg'. Z udv= uv z vdu for di cult integrals, this method can be used to rewrite the integral into an friendlier form. This is the integration by parts formula. Integration by parts is a technique used to evaluate integrals where the integrand is a product of two functions.

For f 2c2[a,b], let fp00 ng

∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx. For instance, if f′ is continuous, then (since g is continuous) the product f′g is continuous; R → r holds z f(x)g0(x)dx = f(x)g(x)− z f0(x)g(x)dx. Theorem for all diﬀerentiable functions g,f :

′′∫ ∫(f g dx f g f g dx)′ = + the left side is easy enough to integrate (we know that integrating a derivative just “undoes” the

∫ (f g)′dx =∫ f ′g +f g′dx ∫ ( f g) ′ d x = ∫ f ′ g + f g ′ d x. The formula for an integration by parts is ⁡ ⁢ ′ ⁡ ⁣ = [⁡ ⁢ ⁡ ()] ′ ⁡ ⁢ ⁡ ⁣ beside the boundary conditions , we notice that the first integral contains two multiplied functions, one which is integrated in the final integral ( g ′ {\displaystyle g'\,} becomes g {\displaystyle g\,} ) and one which is differentiated ( f {\displaystyle f\,} becomes f ′ {\displaystyle f'\,} ). Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways. (f g)′ =f ′g+f g′ ( f g) ′ = f ′ g + f g ′.

Integration by Parts. Integration By Parts Start with the