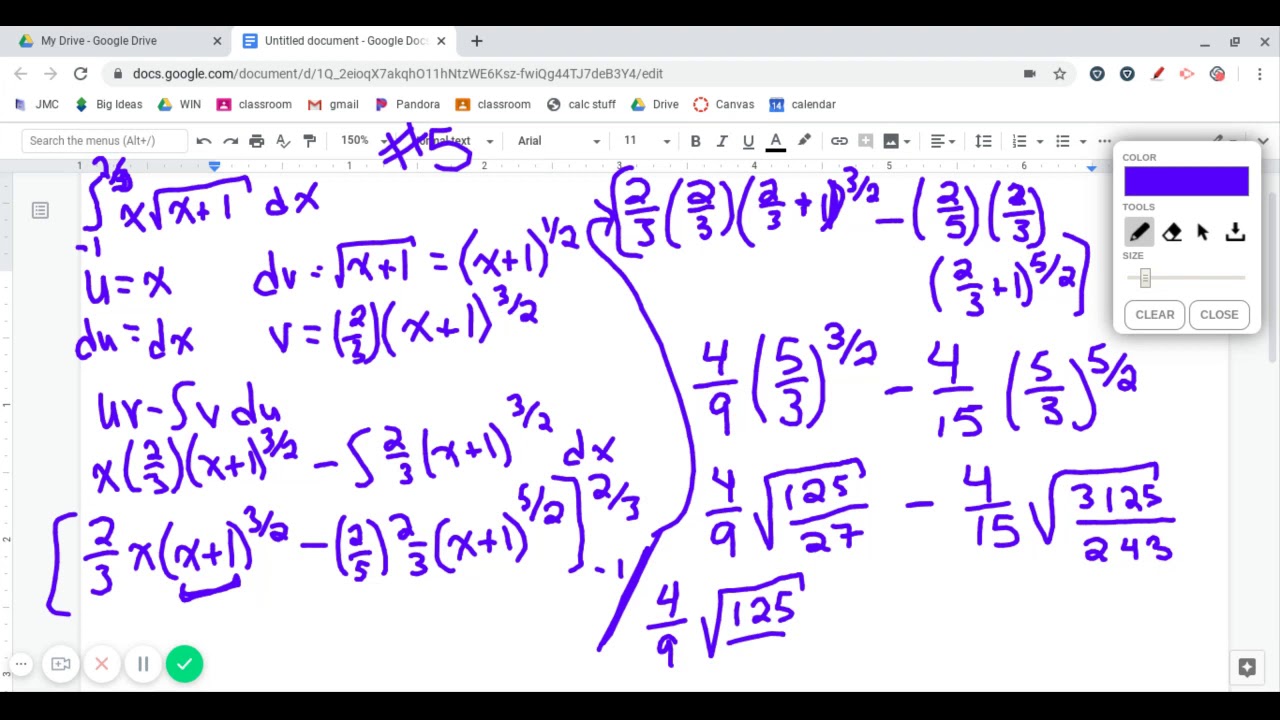
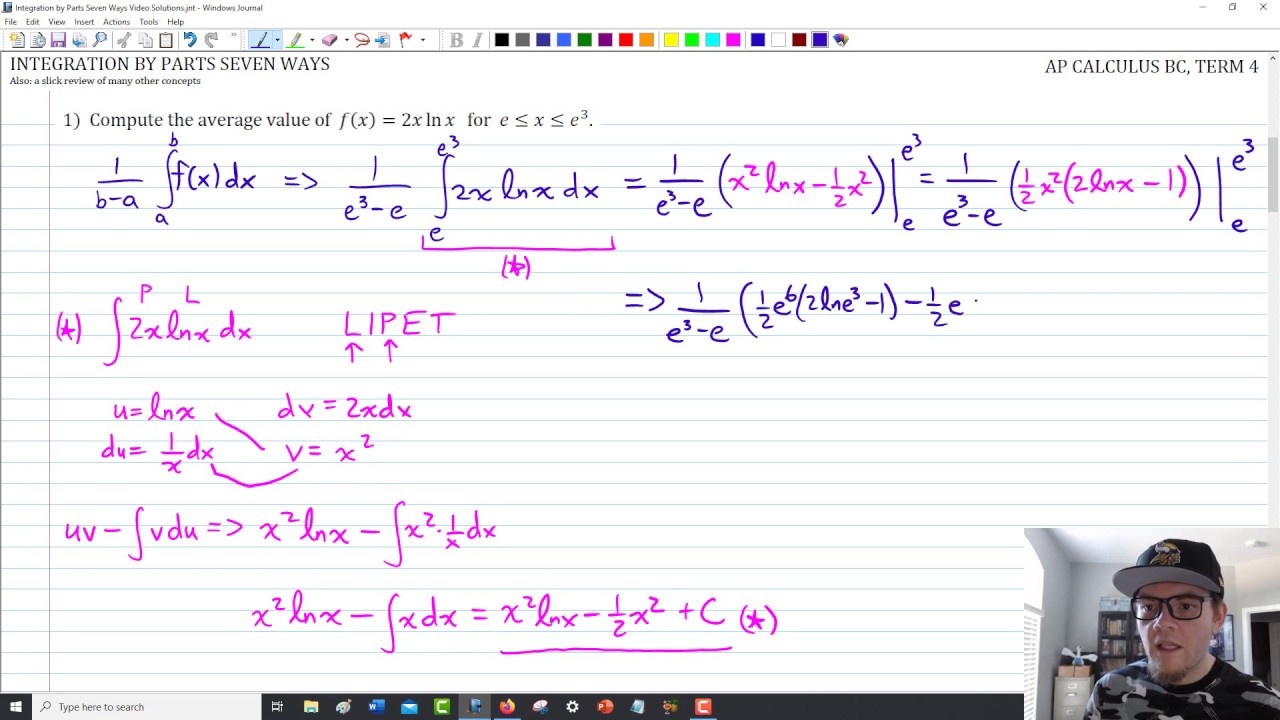
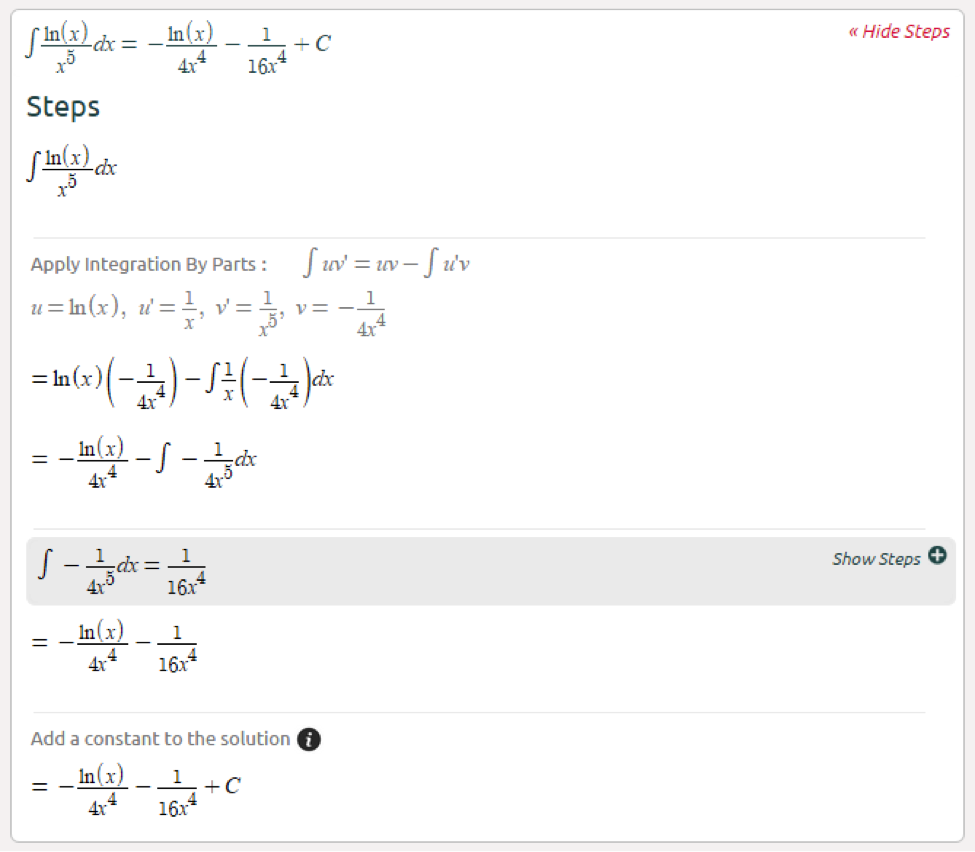
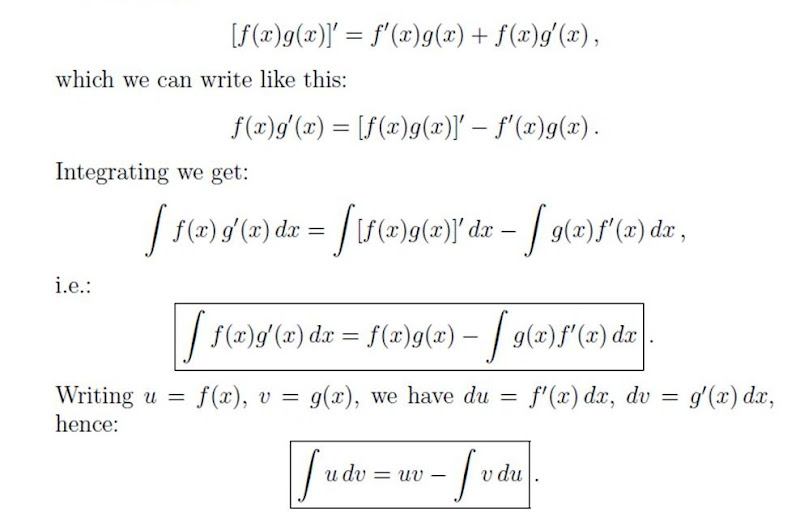Substituting into equation 1, we get. Many exam problems come with a special twist. Applying integration by parts twice over:
Integration By Part Formula / Calculus Integration by
The first one is that you can apply limits after the end of your integrating result as you did in indefinite integration but make sure your variable is the same.
The method of integration by parts all of the following problems use the method of integration by parts.
For example, if , then the differential of is. ∫x2 sin x dx u =x2 (algebraic function) dv =sin x dx (trig function) du =2x dx v =∫sin x dx =−cosx ∫x2 sin x dx =uv−∫vdu =x2 (−cosx) − ∫−cosx 2x dx =−x2 cosx+2 ∫x cosx dx second application of integration by parts: If u and v are any two differentiable functions of a single variable x. ∫ (f g)′dx =∫ f ′g +f g′dx ∫ ( f g) ′ d x = ∫ f ′ g + f g ′ d x.
For example, the following integrals.
Solutions to integration by parts solution 1 : 1 + x 2 = t. ( 2 − 3 x) d x solution. Sometimes integration by parts must be repeated to obtain an answer.
This method uses the fact that the differential of function is.
The following are solutions to the integration by parts practice problems posted november 9. Click here to return to the list of problems. Solution here, we are trying to integrate the product of the functions x and cosx. Then du= sinxdxand v= ex.
We evaluate by integration by parts:
Using the integration by parts formula. ∫ ( 4 x + 7) e x d x. \displaystyle \int (4x+7)e^ {x}dx ∫ (4x+7)exdx using integration by parts. For example, if , then the differential of is.
Then z exsinxdx= exsinx excosx z exsinxdx
Sometimes we may need to try multiple options before we can apply the formula. Let dv = e x dx then v = e x. Click here to return to the list of problems. Example 1 find ˆ xcos(x)dx.
Z xcosxdx = x·sinx− z (1)·sinxdx,i.e.
These methods are used to make complicated integrations easy. Now, integrate both sides of this. (f g)′ =f ′g+f g′ ( f g) ′ = f ′ g + f g ′. Practice problems on integration by parts (with solutions) this problem set is generated by di.
Mathematically, integrating a product of two functions by parts is given as:
Click here to return to the list of problems. Our goal is to make the integral easier. It is important that you can recognise what types of integrals require the method of integration by parts. Notice from the formula that whichever term we let equal u we need to differentiate it in order to.
We have to decide what to assign to f(x) and what to assign to g(x).
Take u = x giving du dx = 1 (by differentiation) and take dv dx = cosx giving v = sinx (by integration), = xsinx− z sinxdx = xsinx−(−cosx)+c, where c is an arbitrary = xsinx+cosx+c constant of. Using the integration by parts formula. Using the formula for integration by parts example find z x cosxdx. To do this integral we will need to use integration by parts so let’s derive the integration by parts formula.
Let’s take an example of \int _ { a } ^ { b } f ( y ) dx ⇒ first, solve the integration of this function
Then du= cosxdxand v= ex. For some of you who want more practice, it™s a good pool of problems. 1)view solution 2)view solution 3)view solution 4)view solutionpart (a): Home→ calculus→ integration of functions→ integration by parts.
[x2 f(x) type] worked example
Of course, we are free to use different letters for variables. I pick the representive ones out. This video aims to show you and then works through an example. Evaluate let u = x 2 then du = 2x dx.
∫ 0 6 (2 +5x)e1 3xdx ∫ 6 0 ( 2 + 5 x).
Rules for solving integration by parts for definite integral limits. The key to integration by parts is making the right choice for f(x) and g(x). ∫ ( 4 x + 7) e x d x = ( 4 x − 3) e x + c. We’ll start with the product rule.
More lessons for calculus math worksheets.
We use integration by parts a second time to evaluate let u = x the du = dx. Integration by parts\(\left({ibp}\right)\) is a special method for integrating products of functions. Use the formula for the integration by parts. Let u= sinx, dv= exdx.
Then z exsinxdx= exsinx z excosxdx now we need to use integration by parts on the second integral.
Solutions to exercises 14 full worked solutions exercise 1. U = 4 x + 7, \displaystyle u=4x+7, u = 4x+7, d v = e x d x. \displaystyle dv=e^ {x}dx dv = exdx. Let’s see it in action.
Then, by the product rule of differentiation, we have;
To use the integration by parts formula we let one of the terms be dv dx and the other be u. The solutions are not proven Let dv = e x dx then v = e x. Let u= cosx, dv= exdx.
\[\int {x\cos xdx} ,\;\;\int {{x^2}{e^x}dx} ,\;\;\int {x\ln xdx} ,\] in which the integrand is the product of two functions can be solved using integration by parts.
There are four steps how to use this formula: