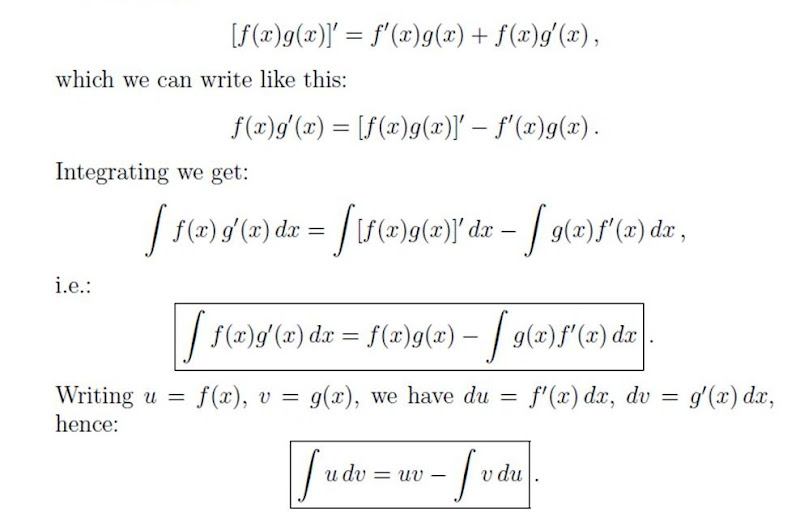Then du= 2lnx x dx;v= 1 2x2: This solution can be found on our substitution handout. Substitute these expressions in 7.18.
Integration problems with solution Sine Trigonometric
2 a b a (s + 1) + b.
Take u = x giving du dx = 1 (by differentiation) and take dv dx = cosx giving v = sinx (by integration), = xsinx− z sinxdx = xsinx−(−cosx)+c, where c is an arbitrary = xsinx+cosx+c constant of integration.
Performing polynomial long division, we have that: This is because of the double angle formula for cosine, cos2x = 1 2sin2 x =) sin2 x = 1 cos2x 2. Rearranging the first we obtain b = 1−a. Substituting u =lnx and du = 1 x dx,youget z 1 xlnx dx = z 1 u du =ln|u|+c =ln|lnx|+c.
Then, z ex sinxdx = ex ·−cosx− z −cosx ·exdx = −cosx·ex + z ex cosxdx.
Many exam problems come with a special twist. Z 2 z s +1 2 ds = (1 + ) ds s2 − 1 s2 − 1 z z 2 = ds + 2 ds s −1 z 2 =s+ 2 ds s −1 using partial fraction on the remaining integral, we get: Substituting u = x−2, u+3=x+1and du = dx, you get z (x+1)(x−2)9dx = z Solution whichever terms we choose for u and dv dx it may not appear that integration by parts is going to produce a simpler integral.
Write down the expressions for u dv and du v.
Sometimes we may need to try multiple options before we can apply the formula. Z lnx x3 dx= lnx 2x2 2 1 + z 2 1 1 2x3 dx= lnx 2x2 1 4x2 2 1 plugging this into the original integral we get: R lnx2 x dx solution. ( 2 − 3 x) d x solution.
This method uses the fact that the differential of function is.
Z b a f(x)g0(x)dx = f(x)g(x)jb a z b a g(x)f0(x)dx example find r xcos(2x)dx r 2 0 xexdx 1 Substituting this into the second gives 14 = 2a +5b = 2a +5(1−a) = 2a +5−5a = 5−3a =⇒ 9 = −3a =⇒ a = −3 =⇒ b = 4 so, ˆ x + 14 (x +5)(x +2) dx = ˆ −3 x +5 + 4 x +2 dx = −3ln|x +5|+4ln|x +2|+c The solutions are not proven Jo 4 since the complex integral is defined in terms of real integrals, we write the inte grand in equation (3) in terms of its real and imaginary parts:
Choose u and du use the integration by parts formula for definite integrals u = dv= e did 2.
Substituting u =lnx and du = 1 x dx,youget z lnx2 x dx = z 2lnx x dx =2 z udu =2· 1 2 u2 +c =(lnx)2 +c. Multiply and divide by 2. (a)let u= x3=2 +1 (b)then du= 3 2 x 1=2dxor 2 3 du= x dx (c)now substitute z x1 =2 p x3 +1 dx = z p x3=2 +1x1=2 dx = z p u 2 3 du = z 2 3 u1=2 du = 2 3 u3=2 2 3 +c = 4 9 u3=2 +c = 4 9 (x3=2 +1)3=2 +c 20. ³ 2 sinx dx u x2 (algebraic function) dv sin x dx (trig function) du 2x dx v ³sin dx cosx ³ 2 sinx dx uv ³vdu 2 ( ) ³ cos 2x dx 2 2 ³cosx dx second application of integration by parts:
For some of you who want more practice, it™s a good pool of problems.
Solutions to exercises 14 full worked solutions exercise 1. 318 chapter 9 / integration 1. Substitute for x and dx. Integrate the new differential vdu.
First identify the parts by reading the differential to be integrated as the product of a function u easily differentiated, and a differential dv easily integrated.
For example, if , then the differential of is. Z x3 p x2 +1 dx (a)let u= x 2 1. D dx [f(x)g(x)] = f(x)g0(x) + g(x)f0(x) we can reverse this rule to get a rule of integration: Z p x q x p x+1 dx you should rewrite the integral as z x1 =2 p x3 +1 dx to help identify u.
390 chapter 6 techniques of integration example 2 integration by substitution find solution consider the substitution which produces to create 2xdxas part of the integral, multiply and divide by 2.
Let’s see it in action. Sometimes integration by parts must be repeated to obtain an answer. I pick the representive ones out. H sin2(x) i 2 = 1 2 2 cos(2x) 2 = 4 h 1 2cos(2x)+cos2(2x) i and integrating gives:
You can check this result by differentiating.
Nevertheless, let us make a choice: Of course, we are free to use different letters for variables. We have to decide what to assign to f(x) and what to assign to g(x). ∫ 0 6 (2 +5x)e1 3xdx ∫ 6 0 ( 2 + 5 x).
Z 2 1 (lnx)2 x3 dx= (lnx) 2x2 2 1 + z 2 1 lnx x3 dx do integration by parts again.
Use an appropriate change of variables to find the integral z (x+1)(x−2)9dx. The integrals of u and v are easy to compute, and we find that Applying the identity for sin2(q), we can write sin4(x) as: Fudv=uv fvdu use the integration by parts formula for indefinite integrals solution 1.
The de nite integral is given by:
The key to integration by parts is making the right choice for f(x) and g(x). ∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u. U then du — 6 du = 9 — 9x2 dx, so that 8x2 dx du. Sometimes integration by parts must be repeated to obtain an answer.
Integration by parts recall the product rule from calculus 1:
Dv dx = sinx and u = ex so that v = z sinxdx = −cosx and du dx = ex. We evaluate by integration by parts: Integration by parts jan 12 learning outcome example find fxé ' dx • recognize when to use integration by parts * recall: Note that this integral can be easily solved using substitution.
Integrate r xex dx by parts.
Our goal is to make the integral easier. Let u= lnx;dv= 1 x3 dx. Substitute u — 3— i)16dx— 8x2 (3x —u17 + c = 17 —(3x3 l) 17 + c i 153 the definite integral in example i (b) can be evaluated more simply by carrying over the cx2. ∫x2 sin x dx u =x2 (algebraic function) dv =sin x dx (trig function) du =2x dx v =∫sin x dx =−cosx ∫x2 sin x dx =uv−∫vdu =x2 (−cosx) − ∫−cosx 2x dx =−x2 cosx+2 ∫x cosx dx second application of integration by parts:
1 3 x2 1 3 2 c 1 3 u3 2 c 1 2 u3 2 3.
Start of with integration by parts. We see that the choice is right because the new integral that we obtain after applying the formula of integration by parts is simpler than the original one: Example 1 find ˆ xcos(x)dx. Let u x dv exdx
But at the moment, we will use this interesting application of integration by parts as seen in the previous problem.
Integration by parts, definite integrals. Example 7.5 find xe xdx. Z xcosxdx = x·sinx− z (1)·sinxdx,i.e. In this case the “right” choice is u = x, dv = ex dx, so du = dx, v = ex.
Z 2 1 (lnx) x3 dx= (lnx) 2 2x2 lnx 2x2 1 4x2 2 1 = 1.
Let u= (lnx)2;dv = 1 x3 dx. Hence example 2 example 3 evaluate 8x (3x solution: Practice problems on integration by parts (with solutions) this problem set is generated by di. Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point.
Z f(x)g0(x)dx = f(x)g(x) z g(x)f0(x)dx or z udv = uv vdu:
Then du= 1 x dx;v= 1 2x2: Z sin4(x)dx = 1 4 z h 1 2cos(2x)+cos2(2x) i dx = 1 4 x sin(2x)+ x 2 + 1 8 sin(4x) +c = 3 8 x 1 4 sin(2x)+ 1 32 sin(4x)+c using the formula for r cos2(2u)du. Using repeated applications of integration by parts: Using repeated applications of integration by parts:
The method of integration by parts all of the following problems use the method of integration by parts.
Z x |{z} u ex dx |{z} dv = x |{z} u e x |{z} v − z. Math 105 921 solutions to integration exercises math 105 921 solutions to integration exercises s2 + 1 z 1) ds s2 − 1 solution: Example find z ex sinxdx. We shall see that the rest of the integrand, 2xdx, will be taken care of automatically in the substitution process, and that this is because 2x is the derivative of that part of the integrand