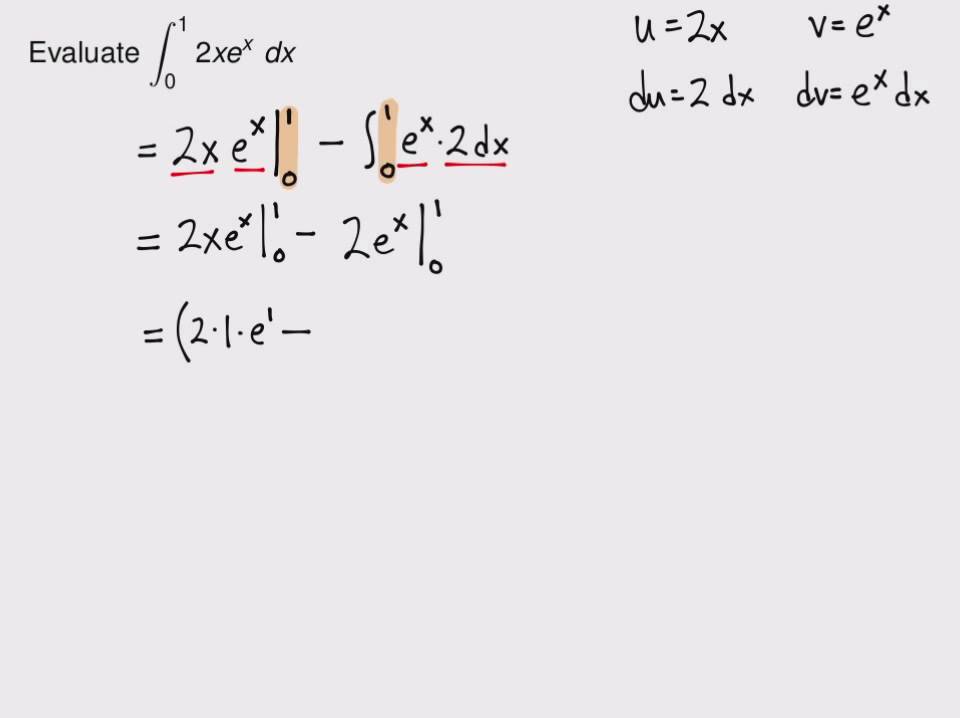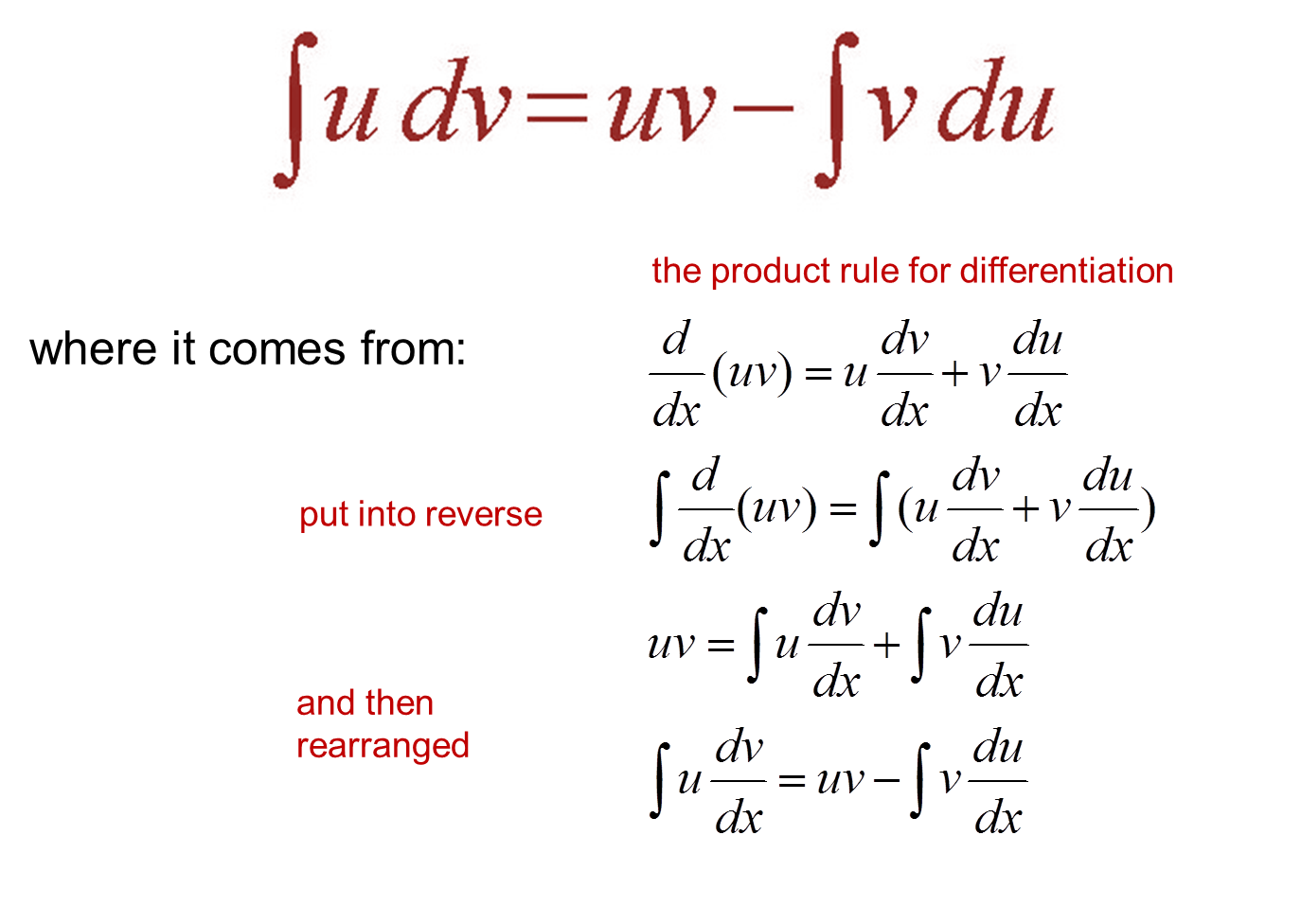Evaluate definite integral by changing limit of integration by parts using rule 2 \int _ { 0 } ^ { 1 } t \sqrt { t + 2 } dt. \[\int {x\cos xdx} ,\;\;\int {{x^2}{e^x}dx} ,\;\;\int {x\ln xdx} ,\] in which the integrand is the product of two functions can be solved using. ∫x 2 ln (x)dx=ln (x)⋅ (⅓)x 3 −∫ (⅓)x 3 ⋅ (1/x) dx.
Integration by Parts Example 2 YouTube
To do this integral we will need to use integration by parts so let’s derive the integration by parts formula.
Choose u and du use the integration by parts formula for definite integrals u = dv= e did 2.
( x) d x = x ln. Integration by parts is a fancy technique for solving integrals. Substituting into equation 1, we get. Of course, we are free to use different letters for variables.
Do these integration and differentiations, and fill the values into the formula:
(f g)′ =f ′g+f g′ ( f g) ′ = f ′ g + f g ′. The method of integration by parts all of the following problems use the method of integration by parts. Previously, we found ∫ x ln. Integration by parts with a definite integral.
X − 1 4 x 2 + c.
Using integration by parts, let u= lnx;dv= (4 1x2)dx. For example, the following integrals. ∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx. All that’s left now is to simplify!
However, subsequent steps are correct.) (the remaining steps are all correct.)
This tutorial runs through an integration by parts example.this video is part of a full free calculus 2 course. Integration by parts jan 12 learning outcome example find fxé ' dx • recognize when to use integration by parts * recall: Integration by parts\(\left({ibp}\right)\) is a special method for integrating products of functions. Y= e x, y= 0, x= 1, x= 0 about x= 1.
Our goal is to make the integral easier.
We’ll start with the product rule. Sometimes we may need to try multiple options before we can apply the formula. Let u = t and dv = \sqrt { t + 2 } dt v = \frac { 2 } { 3 } ( t + 2 ) ^ { 3/2 } Now that we have all the variables, let’s plug them into the integration by parts equation:
Let dv = e x dx then v = e x.
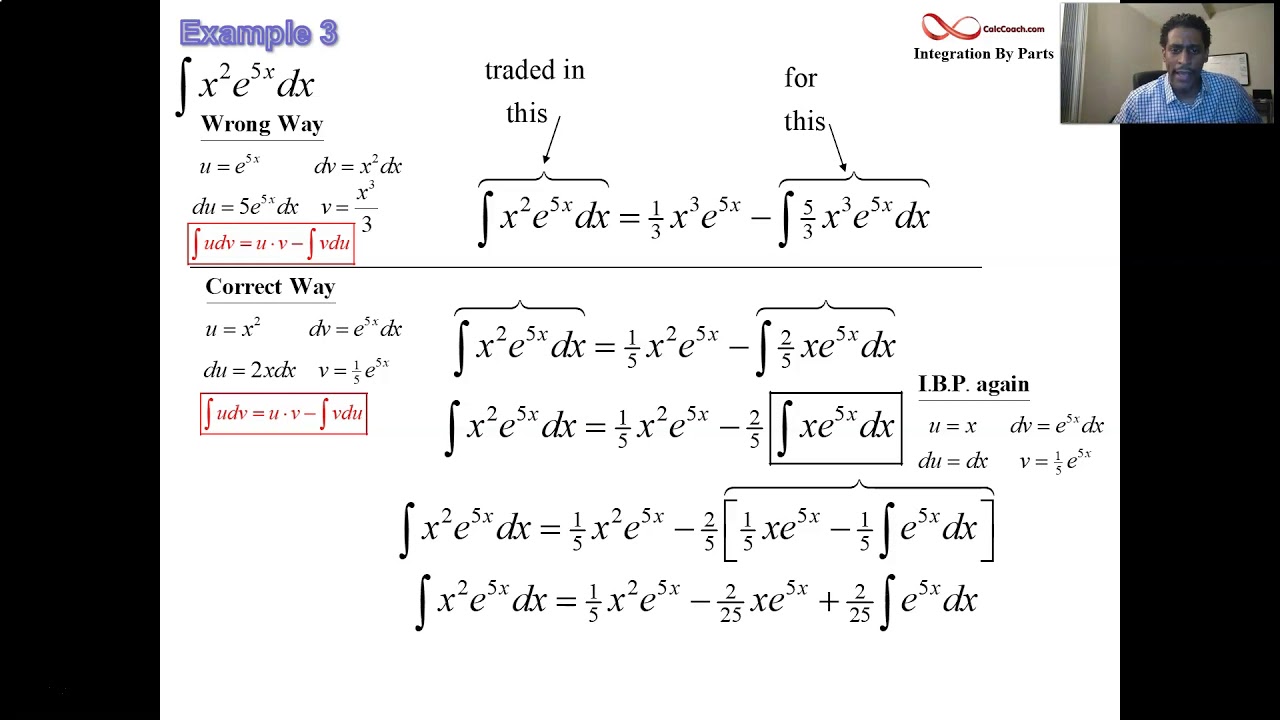
Z 2 1 (4 x2)lnxdx= 4x 1 3 x3 lnx 2 1 z 2 1 4 1 3 x2 dx = 4x 1 3 x3 lnx 4x+ 1 9 x3 2 1 = 16 3 ln2 29 9 15. Examples of integration by parts. Home→ calculus→ integration of functions→ integration by parts. If u and v are any two differentiable functions of a single variable x.
Then, by the product rule of differentiation, we have;
Mathematically, integrating a product of two functions by parts is given as: Integration by parts is one of the method basically used o find the integral when the integrand is a product of two different kind of function. You will see plenty of examples soon, but first let us see the rule: The key to integration by parts is making the right choice for f(x) and g(x).
Using repeated applications of integration by parts:
Integration by parts when the integral of function reappears. This is the currently selected item. This will replicate the denominator and allow us to split the function into two parts.) (please note that there is a typo in the next step. In order to compute the definite integral ∫ 1 e x ln.
Using the fact that integration reverses differentiation we'll arrive at a formula for integrals, called the integration.
To integrate by parts, identify the two functions, and one to integrate, and the other to differentiate. Applying the product rule to solve integrals. Evaluate let u = x 2 then du = 2x dx. Use the method of cylindrical shells to the nd the volume generated by rotating the region bounded by the given curves about the speci ed axis:
( x) d x, it is probably easiest to compute the antiderivative ∫ x ln.
It is usually the last resort when we are trying to solve an integral. U is the function u(x) v is the function v(x) u' is the derivative of the function u(x) $\int$ e cx.{sinsin cx or coscos cx}dx where c is constant. Then complete any further integrals that need to be done.
Using the integration by parts formula.
The course covers integration by table, integ. ∫ 0 6 (2 +5x)e1 3xdx ∫ 6 0 ( 2 + 5 x) e 1 3 x d x solution. So, we are going to begin by recalling the product rule. For example, if , then the differential of is.
∫ (f g)′dx =∫ f ′g +f g′dx ∫ ( f g) ′ d x = ∫ f ′ g + f g ′ d x.
The idea it is based on is very simple: Using the integration by parts formula. ( 2 − 3 x) d x solution. Example 1 find ˆ xcos(x)dx.
We use integration by parts a second time to evaluate let u = x the du = dx.
Let dv = e x dx then v = e x. We have to decide what to assign to f(x) and what to assign to g(x). Fudv=uv fvdu use the integration by parts formula for indefinite integrals solution 1. Let’s see it in action.
Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways.
Now, integrate both sides of this. This method uses the fact that the differential of function is. Sometimes integration by parts must be repeated to obtain an answer. These methods are used to make complicated integrations easy.
∫x2 sin x dx u =x2 (algebraic function) dv =sin x dx (trig function) du =2x dx v =∫sin x dx =−cosx ∫x2 sin x dx =uv−∫vdu =x2 (−cosx) − ∫−cosx 2x dx =−x2 cosx+2 ∫x cosx dx second application of integration by parts: